华东师大版九年级上册数学试题课堂练习 24.2 直角三角形的性质(Word版含答案)
文档属性
| 名称 | 华东师大版九年级上册数学试题课堂练习 24.2 直角三角形的性质(Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 136.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览




文档简介
课堂练习
24.2 直角三角形的性质
如图,在Rt△ABC中,∠ABC=90°,D为AC的中点,BD=6,则AC的长为(
)
A.3
B.6
C.6
D.12
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=(
)
A.2
B.3
C.4
D.2
如图,在Rt△ABC中,∠BAC=90°,点D,E分别为BC,AB的中点,且AC=6
cm,AB=8
cm,则△ADE
周长为(
)
A.10
cm
B.12
cm
C.14
cm
D.16
cm
在Rt△ACB中,∠C=90°,∠A=30°,AB=10,则BC(
)
A.5
B.7.5
C.4
D.10
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为(
)
A.3
B.3.5
C.4
D.4.5
如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为(
)
A.4
B.6
C.4
D.8
如图①,某温室屋顶结构外框为△ABC,立柱AD垂直平分横梁BC,∠B=30°,斜梁AC=4
m,为增大向阳面的面积,将立柱增高并改变位置,使屋顶结构外框变为△EBC(点E在BA的延长线上),立柱EF⊥BC,如图②所示,若EF=3
m,则斜梁增加部分AE的长为(
)
A.0.5
m
B.1
m
C.1.5
m
D.2
m
已知,在等腰△ABC中,AD⊥BC于点D,且AD=BC,则△ABC底角的度数为(
)
A.45°
B.75°
C.45°或15°或75°
D.60°
如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=
.
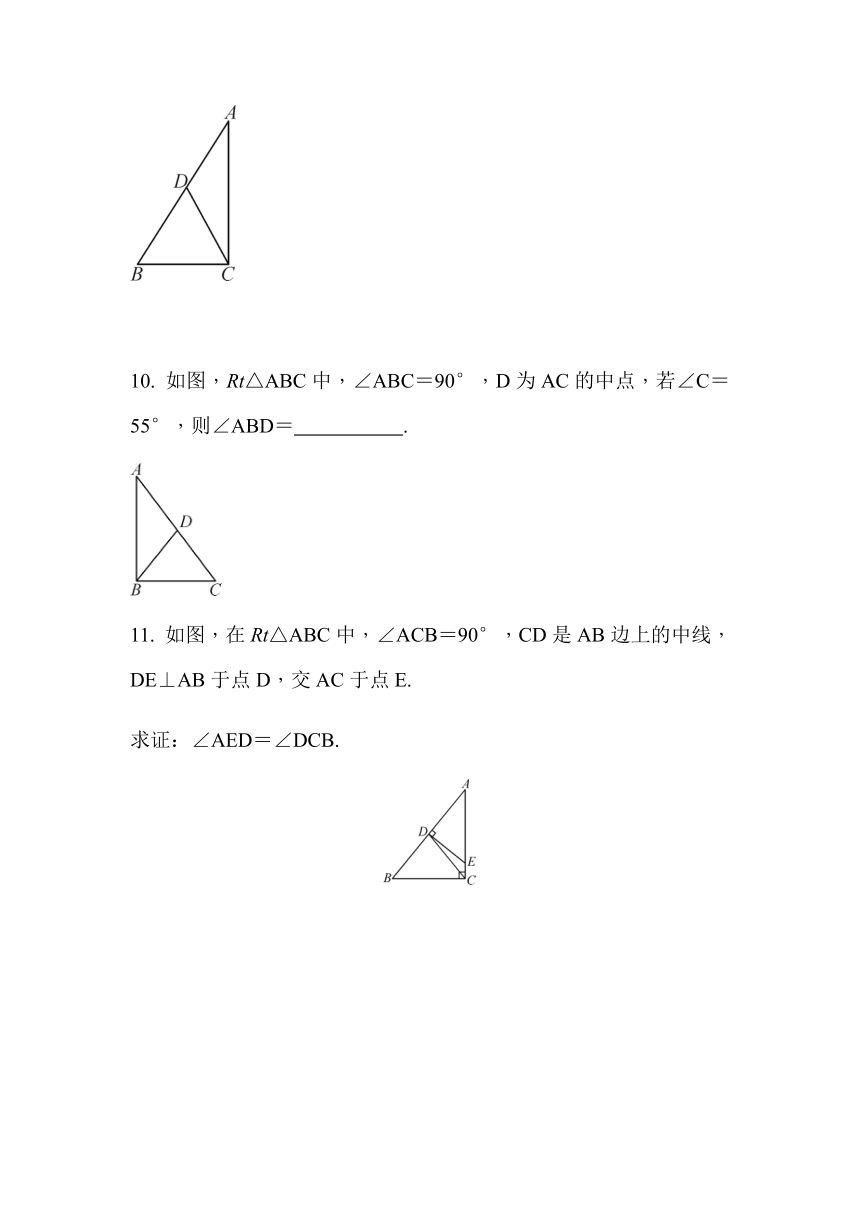
如图,Rt△ABC中,∠ABC=90°,D为AC的中点,若∠C=55°,则∠ABD=
.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
求证:∠AED=∠DCB.
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为
.
如图,已知△ABC中,AB=AC=2,∠B=15°,过点C作CD⊥BA,交BA的延长线于点D,求△ACD的周长和△ABC的面积.
如图,在△ABC中,∠ACB=90°,CD是△ABC的高,∠A=30°,求证:AB=4BD.
在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=BC,则△ABC的顶角的度数为
如图。锐角△ABC中,BE,CF是高,点M,N分别为BC,EF的中点,求证:MN⊥EF。
如图,△ABC中,∠C=60°,AD,
BE是高,AD,
BE交于点O,连
结DE,求证:
DE=AB.
如图,在△ABC中,∠ABC=45°,点H是高AD和高BE的交点,点G,
F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明.
如图,△ABC为等边三角形,AE=CD,AD,
BE相交于点P,BQ⊥
AD于点Q,
PQ=3,
PE=1,求AD的长.
答案:
D
C
B
A
C
B
D
C
3
35°
解:∵在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,∴CD=AB=DB,∴∠B=∠DCB,∵DE⊥AB于点D,∴∠A+∠AED=90°,∵∠A+∠B=90°,∴∠B=∠AED,∴∠AED=∠DCB
4
解:在△ABC中,AB=AC=2,∠B=15°,∴∠B=∠ACB=15°,∴∠DAC=30°.又∵CD⊥BA,∴CD=AC,∴根据勾股定理得到AD==,∴△ACD的周长为AD+CD+AC=+1+2=+3,S△ABC=AB·CD=×2×1=1
解:∵∠ACB=90°,∠A=30°,∴AB=2BC,∠B=60°,又∵CD⊥AB,∴∠DCB=30°,∴BC=2BD,∴AB=2BC=4BD
30°或150°或90°
24.2 直角三角形的性质
如图,在Rt△ABC中,∠ABC=90°,D为AC的中点,BD=6,则AC的长为(
)
A.3
B.6
C.6
D.12
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=(
)
A.2
B.3
C.4
D.2
如图,在Rt△ABC中,∠BAC=90°,点D,E分别为BC,AB的中点,且AC=6
cm,AB=8
cm,则△ADE
周长为(
)
A.10
cm
B.12
cm
C.14
cm
D.16
cm
在Rt△ACB中,∠C=90°,∠A=30°,AB=10,则BC(
)
A.5
B.7.5
C.4
D.10
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为(
)
A.3
B.3.5
C.4
D.4.5
如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为(
)
A.4
B.6
C.4
D.8
如图①,某温室屋顶结构外框为△ABC,立柱AD垂直平分横梁BC,∠B=30°,斜梁AC=4
m,为增大向阳面的面积,将立柱增高并改变位置,使屋顶结构外框变为△EBC(点E在BA的延长线上),立柱EF⊥BC,如图②所示,若EF=3
m,则斜梁增加部分AE的长为(
)
A.0.5
m
B.1
m
C.1.5
m
D.2
m
已知,在等腰△ABC中,AD⊥BC于点D,且AD=BC,则△ABC底角的度数为(
)
A.45°
B.75°
C.45°或15°或75°
D.60°
如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=
.
如图,Rt△ABC中,∠ABC=90°,D为AC的中点,若∠C=55°,则∠ABD=
.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
求证:∠AED=∠DCB.
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为
.
如图,已知△ABC中,AB=AC=2,∠B=15°,过点C作CD⊥BA,交BA的延长线于点D,求△ACD的周长和△ABC的面积.
如图,在△ABC中,∠ACB=90°,CD是△ABC的高,∠A=30°,求证:AB=4BD.
在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=BC,则△ABC的顶角的度数为
如图。锐角△ABC中,BE,CF是高,点M,N分别为BC,EF的中点,求证:MN⊥EF。
如图,△ABC中,∠C=60°,AD,
BE是高,AD,
BE交于点O,连
结DE,求证:
DE=AB.
如图,在△ABC中,∠ABC=45°,点H是高AD和高BE的交点,点G,
F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明.
如图,△ABC为等边三角形,AE=CD,AD,
BE相交于点P,BQ⊥
AD于点Q,
PQ=3,
PE=1,求AD的长.
答案:
D
C
B
A
C
B
D
C
3
35°
解:∵在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,∴CD=AB=DB,∴∠B=∠DCB,∵DE⊥AB于点D,∴∠A+∠AED=90°,∵∠A+∠B=90°,∴∠B=∠AED,∴∠AED=∠DCB
4
解:在△ABC中,AB=AC=2,∠B=15°,∴∠B=∠ACB=15°,∴∠DAC=30°.又∵CD⊥BA,∴CD=AC,∴根据勾股定理得到AD==,∴△ACD的周长为AD+CD+AC=+1+2=+3,S△ABC=AB·CD=×2×1=1
解:∵∠ACB=90°,∠A=30°,∴AB=2BC,∠B=60°,又∵CD⊥AB,∴∠DCB=30°,∴BC=2BD,∴AB=2BC=4BD
30°或150°或90°
