宁夏银川市长庆高级中学2020-2021学年第一学期高二期末考试数学(理)试卷word版含解析
文档属性
| 名称 | 宁夏银川市长庆高级中学2020-2021学年第一学期高二期末考试数学(理)试卷word版含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览




文档简介
宁夏长庆高级中学2020---2021学年第一学期
高二年级数学期末试卷(理科)
满分;150分。考试时间;120分钟。
命题;
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题 共60分)
一、选择题:(本大题共12个小题,每小题5分,共60分,)
1,i是虚数单位,复数的共轭复数是( )
A.2+i
B.2-i
C.-1+2i
D.-1-2i
A【解析】∵===2-i,
∴的共轭复数是2+i.
2.
,则等于(
)
A.
B.
C.
D.
答案;
C
3、若实数,则与的大小关系是
A.
B.
C.
D.不确定
答案;
B.
4,.函数的单调递增区间是
(
)
A.
B.
C.
D.
【答案】C
:∵f′(x)=(x-2)ex,
令f′(x)>0,解得:x>2,
∴f(x)在(2,+∞)递增,
故答案为:C.
5、以下是解决数学问题的思维过程的流程图:
图中①、②两条流程线与“推理与证明”中的思维方法相匹配是(
)
A.①—分析法,②—综合法
B.①—综合法,②—分析法
C.①—综合法,②—反证法
D.①—分析法,②—反证法
、答案B
由题意得,根据分析法是由结论到已知的推理模式,综合法是由已知到未知的推理模式,所以应填①﹣综合法,②﹣分析法,故选B.
6.若f(x)=2xf′(1)+x2,则f′(0)等于( )
(A)2
(B)0
(C)-2
(D)-4
,【解析】f′(x)=2f′(1)+2x,则f′(1)=2f′(1)+2,得f′(1)=-2,所以f′(0)=2f′(1)+0=-4.故选D。
若,则的解集为(
)
A.
B.
C.
D.
【答案】A
【解析】
,又,
故,即,
结合可得.故选A.
7,我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有( )
①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱锥.
A.4个
B.3个
C.2个
D.1个
答案 C
8,已知函数y=xf′(x)的图像如下图所示.下面四个图像中y=f(x)的图像大致是( )
C【解析】由题意知,x∈(0,1)时,f′(x)<0.f(x)为减函数;x∈(1,+∞)时,f′(x)>0.f(x)为增函数;
x∈(-1,0)时,f′(x)<0.f(x)为减函数.
9.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第行的所有数字之和为,若去除所有为1的项,依次构成数列,则此数列的前55项和为(
)
A.4072
B.2026
C.4096
D.2048
【答案】A
【解析】利用n次二项式系数对应杨辉三角形的第n+1行,然后令x=1得到对应项的系数和,结合等比数列和等差数列的公式进行转化求解即可.
【详解】
解:由题意可知:每一行数字和为首项为1,公比为2的等比数列,
则杨辉三角形的前n项和为Sn2n﹣1,
若去除所有的为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成构成一个首项为1,公差为1的等差数列,
则Tn,
可得当n=10,所有项的个数和为55,
则杨辉三角形的前12项的和为S12=212﹣1,
则此数列前55项的和为S12﹣23=4072,
故选:A.
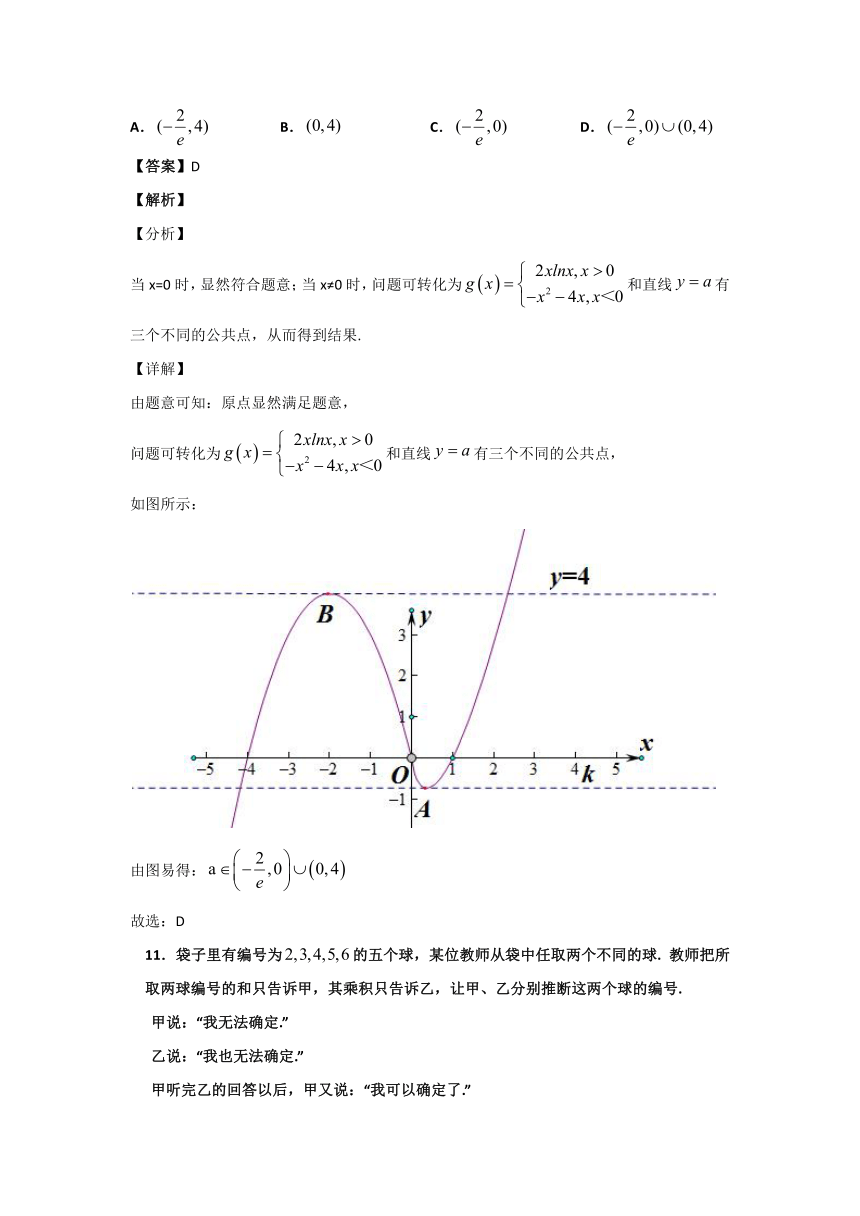
10.若函数的图像和直线有四个不同的公共点,则实数的取值范围是(
)
A.
B.
C.
D.
【答案】D
【解析】
【分析】
当x=0时,显然符合题意;当x≠0时,问题可转化为和直线有三个不同的公共点,从而得到结果.
【详解】
由题意可知:原点显然满足题意,
问题可转化为和直线有三个不同的公共点,
如图所示:
由图易得:
故选:D
11.袋子里有编号为的五个球,某位教师从袋中任取两个不同的球.
教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息,
你可以推断出抽取的两球中
A.一定有3号球
B.一定没有3号球
C.可能有5号球
D.可能有6号球
【答案】D
【解析】
甲说:“我无法确定.”说明两球编号的和可能为7包含(2,5),(3,4),可能为8包含(2,6),(3,5),可能为9包含(3,6),(2,7)
乙说:“我无法确定.”说明两球编号的乘积为12包含(3,4)或(2
,6)
根据以上信息,可以推断出抽取的两球中可能有6号球
故选:D
点睛:本题是一道通俗易懂的合情推理题目,主要考查同学们的逻辑思维能力和推理能力,问题难度不大,认真审题是关键.
12,已知定义在上的函数满足,且对任意(0,3)都有,若,,,则下面结论正确的是(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】
由条件,可知函数关于对称,由对任意(0,3)都有,可知函数在(0,3)时单调递减,然后根据单调性和对称性即可得到的大小.
【详解】
因为,得函数关于对称,
又对任意(0,3)都有,所以函数在(0,3)时单调递减,
因为,所以,
又,所以,所以,故选C.
和第Ⅱ卷(非选择题共90分)
二、填空题:
(本大题共4小题,每小题5分,共20分
)
13.
在复平面内,复数对应的点在第一象限,求实数的取值范围.________.
根据题意得出,
?14.
________.
15.
某商场从生产厂家以每件20元购进一批商品,若该商品零售价为p元,销量Q(单位:件)与零售价p(单位:元)有如下关系:
Q=8300-170p-p2,则该商品零售价定为___30_____元时利润最大。
16,已知为正实数,直线与曲线相切,则的最小值为__________.
【答案】
【解析】
【分析】
设切点的坐标为,利用导数的几何意义,求得,再利用基本不等式,即可求解的最小值,得到答案.
【详解】
由题意,设切点的坐标为,
又由函数,则,
又由切线的方程可得切线的斜率为1,则,解得,
即切点的横坐标为,所以切点为,
代入直线方程,得,
又因为、为正实数,
则,
当且仅当,即时,取得最小值.
故答案为.
三、解答题:
(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.
(本小题10分)17、已知函数f(x)=求其在点(1,2)处的切线与函数g(x)=x2围成的图形的面积.
解析:∵(1,2)为曲线f(x)=上的点,设过点(1,2)处的切线的斜率为k,则
k=f′(1)=(3x2-2x+1)|x=1=2
∴在点(1,2)处的切线方程为y-2=2(x-1),即y=2x
2分
由y=2x
(y=x2,)可得交点A(2,4).
4分
∴y=2x与函数g(x)=x2围成的图形的面积
7分
S==x3
(1)0
(2)=4-3
(8)=3
(4)
10分
18.
(本小题12分)设x,y为正实数,且x+y=1,
求证(1+)(1+)≧9
19.
(本小题12分)已知函数.
(1)求函数的极值;
(2)当时,求函数的最值.
【答案】(1)的极大值为,极小值为;(2)的最大值为,最小值为
【解析】
【分析】
(1)直接利用导数求函数的极值.(2)比较端点函数值和极值的大小即得解.
【详解】
(1)f′(x)=3x2-12=3(x+2)(x-2),
令f′(x)=3x2-12=3(x+2)(x-2)=0,解得x=2或x=-2,
x,f′(x),f(x)的变化如下表:
x
(-∞,-2)
-2
(-2,2)
2
(2,+∞)
f′(x)
+
0
-
0
+
f(x)
单调递增
16
单调递减
-16
单调递增
∴函数f(x)的极大值为f(-2)=16,极小值为f(2)=-16.
(2)由(1)知,f(-2)=16,f(2)=-16,又f(-3)=9,f(3)=-9,
∴当x∈[-3,3]时,函数f(x)的最大值为f(-2)=16,最小值为f(2)=-16.
20.
(本小题12分)中国民间十字绣有着悠久的历史,如下图,①②③④为十字绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图案包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式猜测出f(n)的表达式;
(3)求+++…+(n≥2)的值.
解:(1)按所给图案的规律画出第五个图如下:
由图可得f(5)=41.
(2)可得f(2)-f(1)=4×1;
f(3)-f(2)=8=4×2;
f(4)-f(3)=12=4×3;
f(5)-f(4)=16=4×4;
……
由上式规律,可得f(n)-f(n-1)=4(n-1).
由以上各式相加可得f(n)-f(1)=4[1+2+…+(n-1)]=4×=2n2-2n,
又f(1)=1,∴f(n)=2n2-2n+1.
(3)当n≥2时,===,
∴原式=+1-+-+-+…+-=1+=-.
备选
.已知函数f(x)=ax3+bx+c在点x=2处取得极值c-16.
(1)求a,b的值;
(2)若f(x)有极大值28,求f(x)在[-3,3]上的最小值.
[解]
(1)因为f(x)=ax3+bx+c,
故f′(x)=3ax2+b.
2分
由于f(x)在点x=2处取得极值c-16,
故有f(2
(f′(2)即8a+2b+c=c-16,
(12a+b=0,)
化简得4a+b=-8,
(12a+b=0,)解得b=-12.
(a=1,)
5分
(2)由(1)知f(x)=x3-12x+c,
f′(x)=3x2-12=3(x-2)(x+2),
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,
故f(x)在(-∞,-2)上为增函数;
7分
当x∈(-2,2)时,f′(x)<0,
故f(x)在(-2,2)上为减函数;
8分
当x∈(2,+∞)时,f′(x)>0,
故f(x)在(2,+∞)上为增函数.
由此可知f(x)在x=-2处取得极大值,
f(-2)=16+c,
f(x)在x=2处取得极小值f(2)=c-16.
由题设条件知16+c=28,解得c=12.
10分
此时f(-3)=9+c=21,f(3)=-9+c=3,
f(2)=-16+c=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4.
12分
21.
(本小题12分)
设函数
(I)求曲线在点处的切线方程;
(II)设,若函数有三个不同零点,求c的取值范围;
【答案】(Ⅰ);(Ⅱ)
【解析】(I)由,得.
因为,,
所以曲线在点处的切线方程为.
(II)当时,,
所以.
令,得,解得或.
与在区间上的情况如下:
所以,当且时,存在,,
,使得.
由的单调性知,当且仅当时,函数有三个不同零点.
22.
(本小题12分)已知函数f(x)=-2xlnx+x2-2ax+a2,其中a>0.
(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(2)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
解析 (1)由已知,函数f(x)的定义域为(0,+∞),
g(x)=f′(x)=2(x-1-lnx-a),
所以g′(x)=2-=.
当x∈(0,1)时,g′(x)<0,g(x)单调递减;
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增.
(2)由f′(x)=2(x-1-lnx-a)=0,解得a=x-1-lnx.
令φ(x)=-2xlnx+x2-2x(x-1-lnx)+(x-1-lnx)2=(1+lnx)2-2xlnx,
则φ(1)=1>0,φ(e)=2(2-e)<0.
于是存在x0∈(1,e),使得φ(x0)=0.
令a0=x0-1-lnx0=u(x0),其中u(x)=x-1-lnx(x≥1).
由u′(x)=1-≥0知,函数u(x)在区间(1,+∞)上单调递增,
故0=u(1)当a=a0时,有f′(x0)=0,f(x0)=φ(x0)=0.
再由(1)知,f′(x)在区间(1,+∞)上单调递增,
当x∈(1,x0)时,f′(x)<0,从而f(x)>f(x0)=0;
当x∈(x0,+∞)时,f′(x)>0,从而f(x)>f(x0)=0;
又当x∈(0,1]时,f(x)=(x-a0)2-2xlnx>0.
故x∈(0,+∞)时,f(x)≥0.
综上所述,存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
高二年级数学期末试卷(理科)
满分;150分。考试时间;120分钟。
命题;
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题 共60分)
一、选择题:(本大题共12个小题,每小题5分,共60分,)
1,i是虚数单位,复数的共轭复数是( )
A.2+i
B.2-i
C.-1+2i
D.-1-2i
A【解析】∵===2-i,
∴的共轭复数是2+i.
2.
,则等于(
)
A.
B.
C.
D.
答案;
C
3、若实数,则与的大小关系是
A.
B.
C.
D.不确定
答案;
B.
4,.函数的单调递增区间是
(
)
A.
B.
C.
D.
【答案】C
:∵f′(x)=(x-2)ex,
令f′(x)>0,解得:x>2,
∴f(x)在(2,+∞)递增,
故答案为:C.
5、以下是解决数学问题的思维过程的流程图:
图中①、②两条流程线与“推理与证明”中的思维方法相匹配是(
)
A.①—分析法,②—综合法
B.①—综合法,②—分析法
C.①—综合法,②—反证法
D.①—分析法,②—反证法
、答案B
由题意得,根据分析法是由结论到已知的推理模式,综合法是由已知到未知的推理模式,所以应填①﹣综合法,②﹣分析法,故选B.
6.若f(x)=2xf′(1)+x2,则f′(0)等于( )
(A)2
(B)0
(C)-2
(D)-4
,【解析】f′(x)=2f′(1)+2x,则f′(1)=2f′(1)+2,得f′(1)=-2,所以f′(0)=2f′(1)+0=-4.故选D。
若,则的解集为(
)
A.
B.
C.
D.
【答案】A
【解析】
,又,
故,即,
结合可得.故选A.
7,我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有( )
①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱锥.
A.4个
B.3个
C.2个
D.1个
答案 C
8,已知函数y=xf′(x)的图像如下图所示.下面四个图像中y=f(x)的图像大致是( )
C【解析】由题意知,x∈(0,1)时,f′(x)<0.f(x)为减函数;x∈(1,+∞)时,f′(x)>0.f(x)为增函数;
x∈(-1,0)时,f′(x)<0.f(x)为减函数.
9.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第行的所有数字之和为,若去除所有为1的项,依次构成数列,则此数列的前55项和为(
)
A.4072
B.2026
C.4096
D.2048
【答案】A
【解析】利用n次二项式系数对应杨辉三角形的第n+1行,然后令x=1得到对应项的系数和,结合等比数列和等差数列的公式进行转化求解即可.
【详解】
解:由题意可知:每一行数字和为首项为1,公比为2的等比数列,
则杨辉三角形的前n项和为Sn2n﹣1,
若去除所有的为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成构成一个首项为1,公差为1的等差数列,
则Tn,
可得当n=10,所有项的个数和为55,
则杨辉三角形的前12项的和为S12=212﹣1,
则此数列前55项的和为S12﹣23=4072,
故选:A.
10.若函数的图像和直线有四个不同的公共点,则实数的取值范围是(
)
A.
B.
C.
D.
【答案】D
【解析】
【分析】
当x=0时,显然符合题意;当x≠0时,问题可转化为和直线有三个不同的公共点,从而得到结果.
【详解】
由题意可知:原点显然满足题意,
问题可转化为和直线有三个不同的公共点,
如图所示:
由图易得:
故选:D
11.袋子里有编号为的五个球,某位教师从袋中任取两个不同的球.
教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息,
你可以推断出抽取的两球中
A.一定有3号球
B.一定没有3号球
C.可能有5号球
D.可能有6号球
【答案】D
【解析】
甲说:“我无法确定.”说明两球编号的和可能为7包含(2,5),(3,4),可能为8包含(2,6),(3,5),可能为9包含(3,6),(2,7)
乙说:“我无法确定.”说明两球编号的乘积为12包含(3,4)或(2
,6)
根据以上信息,可以推断出抽取的两球中可能有6号球
故选:D
点睛:本题是一道通俗易懂的合情推理题目,主要考查同学们的逻辑思维能力和推理能力,问题难度不大,认真审题是关键.
12,已知定义在上的函数满足,且对任意(0,3)都有,若,,,则下面结论正确的是(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】
由条件,可知函数关于对称,由对任意(0,3)都有,可知函数在(0,3)时单调递减,然后根据单调性和对称性即可得到的大小.
【详解】
因为,得函数关于对称,
又对任意(0,3)都有,所以函数在(0,3)时单调递减,
因为,所以,
又,所以,所以,故选C.
和第Ⅱ卷(非选择题共90分)
二、填空题:
(本大题共4小题,每小题5分,共20分
)
13.
在复平面内,复数对应的点在第一象限,求实数的取值范围.________.
根据题意得出,
?14.
________.
15.
某商场从生产厂家以每件20元购进一批商品,若该商品零售价为p元,销量Q(单位:件)与零售价p(单位:元)有如下关系:
Q=8300-170p-p2,则该商品零售价定为___30_____元时利润最大。
16,已知为正实数,直线与曲线相切,则的最小值为__________.
【答案】
【解析】
【分析】
设切点的坐标为,利用导数的几何意义,求得,再利用基本不等式,即可求解的最小值,得到答案.
【详解】
由题意,设切点的坐标为,
又由函数,则,
又由切线的方程可得切线的斜率为1,则,解得,
即切点的横坐标为,所以切点为,
代入直线方程,得,
又因为、为正实数,
则,
当且仅当,即时,取得最小值.
故答案为.
三、解答题:
(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.
(本小题10分)17、已知函数f(x)=求其在点(1,2)处的切线与函数g(x)=x2围成的图形的面积.
解析:∵(1,2)为曲线f(x)=上的点,设过点(1,2)处的切线的斜率为k,则
k=f′(1)=(3x2-2x+1)|x=1=2
∴在点(1,2)处的切线方程为y-2=2(x-1),即y=2x
2分
由y=2x
(y=x2,)可得交点A(2,4).
4分
∴y=2x与函数g(x)=x2围成的图形的面积
7分
S==x3
(1)0
(2)=4-3
(8)=3
(4)
10分
18.
(本小题12分)设x,y为正实数,且x+y=1,
求证(1+)(1+)≧9
19.
(本小题12分)已知函数.
(1)求函数的极值;
(2)当时,求函数的最值.
【答案】(1)的极大值为,极小值为;(2)的最大值为,最小值为
【解析】
【分析】
(1)直接利用导数求函数的极值.(2)比较端点函数值和极值的大小即得解.
【详解】
(1)f′(x)=3x2-12=3(x+2)(x-2),
令f′(x)=3x2-12=3(x+2)(x-2)=0,解得x=2或x=-2,
x,f′(x),f(x)的变化如下表:
x
(-∞,-2)
-2
(-2,2)
2
(2,+∞)
f′(x)
+
0
-
0
+
f(x)
单调递增
16
单调递减
-16
单调递增
∴函数f(x)的极大值为f(-2)=16,极小值为f(2)=-16.
(2)由(1)知,f(-2)=16,f(2)=-16,又f(-3)=9,f(3)=-9,
∴当x∈[-3,3]时,函数f(x)的最大值为f(-2)=16,最小值为f(2)=-16.
20.
(本小题12分)中国民间十字绣有着悠久的历史,如下图,①②③④为十字绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图案包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式猜测出f(n)的表达式;
(3)求+++…+(n≥2)的值.
解:(1)按所给图案的规律画出第五个图如下:
由图可得f(5)=41.
(2)可得f(2)-f(1)=4×1;
f(3)-f(2)=8=4×2;
f(4)-f(3)=12=4×3;
f(5)-f(4)=16=4×4;
……
由上式规律,可得f(n)-f(n-1)=4(n-1).
由以上各式相加可得f(n)-f(1)=4[1+2+…+(n-1)]=4×=2n2-2n,
又f(1)=1,∴f(n)=2n2-2n+1.
(3)当n≥2时,===,
∴原式=+1-+-+-+…+-=1+=-.
备选
.已知函数f(x)=ax3+bx+c在点x=2处取得极值c-16.
(1)求a,b的值;
(2)若f(x)有极大值28,求f(x)在[-3,3]上的最小值.
[解]
(1)因为f(x)=ax3+bx+c,
故f′(x)=3ax2+b.
2分
由于f(x)在点x=2处取得极值c-16,
故有f(2
(f′(2)即8a+2b+c=c-16,
(12a+b=0,)
化简得4a+b=-8,
(12a+b=0,)解得b=-12.
(a=1,)
5分
(2)由(1)知f(x)=x3-12x+c,
f′(x)=3x2-12=3(x-2)(x+2),
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,
故f(x)在(-∞,-2)上为增函数;
7分
当x∈(-2,2)时,f′(x)<0,
故f(x)在(-2,2)上为减函数;
8分
当x∈(2,+∞)时,f′(x)>0,
故f(x)在(2,+∞)上为增函数.
由此可知f(x)在x=-2处取得极大值,
f(-2)=16+c,
f(x)在x=2处取得极小值f(2)=c-16.
由题设条件知16+c=28,解得c=12.
10分
此时f(-3)=9+c=21,f(3)=-9+c=3,
f(2)=-16+c=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4.
12分
21.
(本小题12分)
设函数
(I)求曲线在点处的切线方程;
(II)设,若函数有三个不同零点,求c的取值范围;
【答案】(Ⅰ);(Ⅱ)
【解析】(I)由,得.
因为,,
所以曲线在点处的切线方程为.
(II)当时,,
所以.
令,得,解得或.
与在区间上的情况如下:
所以,当且时,存在,,
,使得.
由的单调性知,当且仅当时,函数有三个不同零点.
22.
(本小题12分)已知函数f(x)=-2xlnx+x2-2ax+a2,其中a>0.
(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(2)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
解析 (1)由已知,函数f(x)的定义域为(0,+∞),
g(x)=f′(x)=2(x-1-lnx-a),
所以g′(x)=2-=.
当x∈(0,1)时,g′(x)<0,g(x)单调递减;
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增.
(2)由f′(x)=2(x-1-lnx-a)=0,解得a=x-1-lnx.
令φ(x)=-2xlnx+x2-2x(x-1-lnx)+(x-1-lnx)2=(1+lnx)2-2xlnx,
则φ(1)=1>0,φ(e)=2(2-e)<0.
于是存在x0∈(1,e),使得φ(x0)=0.
令a0=x0-1-lnx0=u(x0),其中u(x)=x-1-lnx(x≥1).
由u′(x)=1-≥0知,函数u(x)在区间(1,+∞)上单调递增,
故0=u(1)
再由(1)知,f′(x)在区间(1,+∞)上单调递增,
当x∈(1,x0)时,f′(x)<0,从而f(x)>f(x0)=0;
当x∈(x0,+∞)时,f′(x)>0,从而f(x)>f(x0)=0;
又当x∈(0,1]时,f(x)=(x-a0)2-2xlnx>0.
故x∈(0,+∞)时,f(x)≥0.
综上所述,存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
同课章节目录
