人教版数学七年级上册导学案:4.3.3余角和补角(2)(Word版无答案)
文档属性
| 名称 | 人教版数学七年级上册导学案:4.3.3余角和补角(2)(Word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 08:00:12 | ||
图片预览

文档简介
§4.3.3余角和补角第二课时-----方位角
一、课标对本课时的具体要求:
在平面上,能用方位角描述物体的大体方位。
二、本课时的知识网络
三、本课时的重点、难点
重点:能确定具体物体的方位。
难点:正确使用方位角确定位置。
四、学习目标
1、认识方位角;
2、能确定具体物体的方位.
五、学习过程
(一)多媒体出示自学指导:(5分钟)
认真看课本P138页的内容,理解方位角的表示方法,三分钟后比一比,看谁能又快又准的用方位角画出物体所在的方位。
(学生根据要求,自读课本,完成学案所给的问题,在明确的引领下引导学生积极参与探讨和学习)
(二)展示交流
探究新知(10分钟)
活动一:思考下列问题并在小组内交流:
1、你知道表示方向的一个成语吗?
“四面”指
、
、
、
.“八方”指
、
、
、
和
、
、
、
.
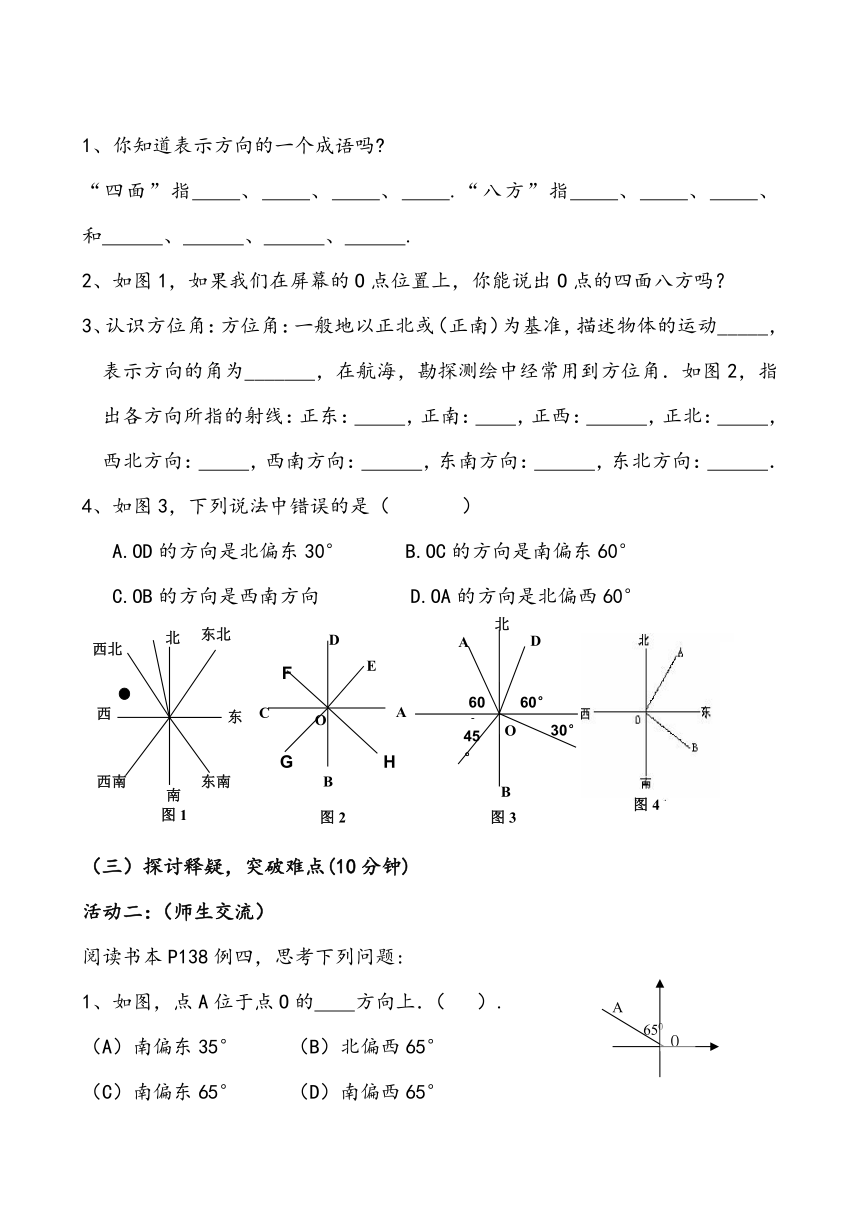
2、如图1,如果我们在屏幕的O点位置上,你能说出O点的四面八方吗?
3、认识方位角:方位角:一般地以正北或(正南)为基准,描述物体的运动_____,表示方向的角为_______,在航海,勘探测绘中经常用到方位角.如图2,指出各方向所指的射线:正东:
,正南:
,正西:
,正北:
,西北方向:
,西南方向:
,东南方向:
,东北方向:
.
4、如图3,下列说法中错误的是(
)
A.OD的方向是北偏东30°
B.OC的方向是南偏东60°
C.OB的方向是西南方向
D.OA的方向是北偏西60°
(三)探讨释疑,突破难点(10分钟)
活动二:(师生交流)
阅读书本P138例四,思考下列问题:
1、如图,点A位于点O的
方向上.(
).
(A)南偏东35°
(B)北偏西65°
(C)南偏东65°
(D)南偏西65°
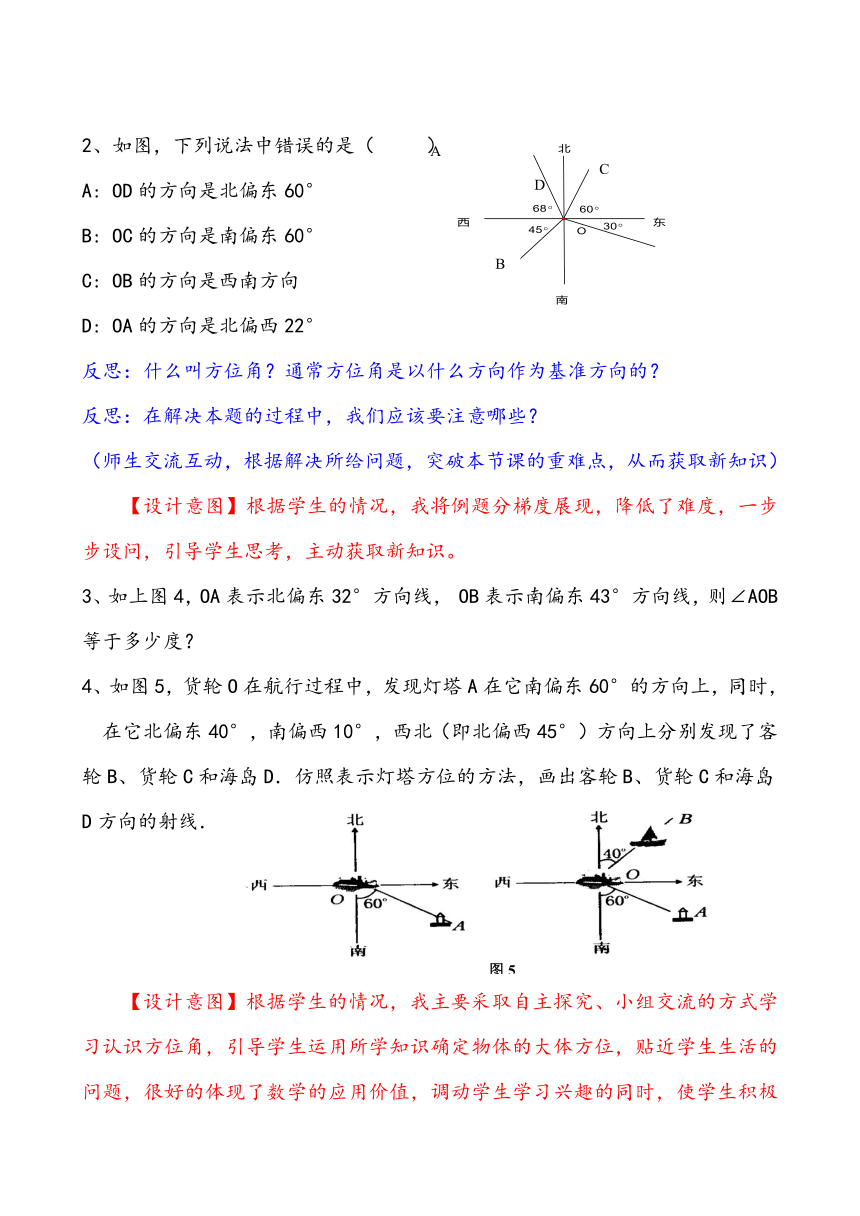
2、如图,下列说法中错误的是(
)
A:
OD的方向是北偏东60°
B:
OC的方向是南偏东60°
C:
OB的方向是西南方向
D:
OA的方向是北偏西22°
反思:什么叫方位角?通常方位角是以什么方向作为基准方向的?
反思:在解决本题的过程中,我们应该要注意哪些?
(师生交流互动,根据解决所给问题,突破本节课的重难点,从而获取新知识)
【设计意图】根据学生的情况,我将例题分梯度展现,降低了难度,一步步设问,引导学生思考,主动获取新知识。
3、如上图4,OA表示北偏东32°方向线,
OB表示南偏东43°方向线,则∠AOB等于多少度?
4、如图5,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出客轮B、货轮C和海岛D方向的射线.
【设计意图】根据学生的情况,我主要采取自主探究、小组交流的方式学习认识方位角,引导学生运用所学知识确定物体的大体方位,贴近学生生活的问题,很好的体现了数学的应用价值,调动学生学习兴趣的同时,使学生积极参与学习活动。
教师在这一环节中参与到学生的讨论交流中,及时引导,归纳总结出方位角的画法及应用,培养学生的合作交流能力的同时,也让学生亲自体验了知识的产生过程,品尝到了学习的乐趣。
(四)学以致用
品尝成功(10分钟)
本着低起点、小台阶的原则,将练习分层次设置,以帮助学生实现从易到难、从会学到会用、从知识到能力的迁移,我设置了以下两个练习。
做一做——夯实基础
1、如图7,(1)射线OA表示________的方向;(2)OB表示______方向或________方向;(3)OC表示南_______方向.
2、如图8,下列说法错误的是(
)
A.
OA的方向是北偏西22°
B.
OB方向是西南方向
C.
OC的方向是南偏东60°
D.
OD的方向是北偏东60°
3、如图9,OA表示北偏东30°方向的一条射线,依照这条射线,画出表示下列方向的射线.
(1)南偏东25°;
(2)北偏西60°;
(3)东南方向.
想一想——发散思维
4、A看B的方向是北偏东21°,那么B看A的方向(
)
A:南偏东69°
B:南偏西69°
C:南偏东21°
D:南偏西21°
5、小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西
40°方向走了4米,到达点C,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离。
【设计意图】这些练习的设置,可以让学生多角度,全方位发挥其思维的深度和广度,拓宽学生的认知领域,培养学生的发散思维能力
(五)达标测试
(9分钟)
为了实现人人都学有价值的数学,不同层次学生都能得到发展,我设置了必做题和选做题,让学生品尝成功,树立信心。
必做题:(认真仔细,你一定有更大的收获!)
1、如图10,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于多少?
2、如图,OA表示北偏东32°方向线,
OB表示南偏东43°方向线,则∠AOB等于
3、在点O
北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是(
)
A:100°
B:70°
C:180°
D:140°
4、灯塔A在灯塔B的南偏东60°方向上,A、B相距30海里,轮船C在B的正南方向,在灯塔A的南偏西60°方向上,通过画图(用1个单位代表10海里)确定轮船C的位置,求∠BAC和∠ACB的度数,并求出轮船C与灯塔B的距离.
再攀新高峰:(选做题)
5、(1)如图6,xx中学2014年5月6日将举行运动会,一名服务的同学往返于百米起跑点A、终点B(A、B位于东西方向)及检录处C,他在A处看C点位于北偏东60°的方向上,在B点处看C点位于西北方向上(即北偏西45°),你能确定检录处C的位置么?
(2)检录处C在起点A的北偏东60°的方向上,那么起点A在检录处C的什么方向上呢?(
)
A.南偏东30°
B.南偏西30°
C.南偏东60°
D.南偏西60°
(3)如果测的AB的图上距离是4Cm,AC的图上距离是6Cm,那么,一个服务同学从A点跑到C点,在从C点跑回A点,他实际上跑了多少路程?
(学生独立完成,小组交流订正,独立完成整理到错题集上)
学后反思
1、我学会的(
知
识
、方
法)有:
。
2、注意点有
。
3、对自己想说的一句话是:
。
一、课标对本课时的具体要求:
在平面上,能用方位角描述物体的大体方位。
二、本课时的知识网络
三、本课时的重点、难点
重点:能确定具体物体的方位。
难点:正确使用方位角确定位置。
四、学习目标
1、认识方位角;
2、能确定具体物体的方位.
五、学习过程
(一)多媒体出示自学指导:(5分钟)
认真看课本P138页的内容,理解方位角的表示方法,三分钟后比一比,看谁能又快又准的用方位角画出物体所在的方位。
(学生根据要求,自读课本,完成学案所给的问题,在明确的引领下引导学生积极参与探讨和学习)
(二)展示交流
探究新知(10分钟)
活动一:思考下列问题并在小组内交流:
1、你知道表示方向的一个成语吗?
“四面”指
、
、
、
.“八方”指
、
、
、
和
、
、
、
.
2、如图1,如果我们在屏幕的O点位置上,你能说出O点的四面八方吗?
3、认识方位角:方位角:一般地以正北或(正南)为基准,描述物体的运动_____,表示方向的角为_______,在航海,勘探测绘中经常用到方位角.如图2,指出各方向所指的射线:正东:
,正南:
,正西:
,正北:
,西北方向:
,西南方向:
,东南方向:
,东北方向:
.
4、如图3,下列说法中错误的是(
)
A.OD的方向是北偏东30°
B.OC的方向是南偏东60°
C.OB的方向是西南方向
D.OA的方向是北偏西60°
(三)探讨释疑,突破难点(10分钟)
活动二:(师生交流)
阅读书本P138例四,思考下列问题:
1、如图,点A位于点O的
方向上.(
).
(A)南偏东35°
(B)北偏西65°
(C)南偏东65°
(D)南偏西65°
2、如图,下列说法中错误的是(
)
A:
OD的方向是北偏东60°
B:
OC的方向是南偏东60°
C:
OB的方向是西南方向
D:
OA的方向是北偏西22°
反思:什么叫方位角?通常方位角是以什么方向作为基准方向的?
反思:在解决本题的过程中,我们应该要注意哪些?
(师生交流互动,根据解决所给问题,突破本节课的重难点,从而获取新知识)
【设计意图】根据学生的情况,我将例题分梯度展现,降低了难度,一步步设问,引导学生思考,主动获取新知识。
3、如上图4,OA表示北偏东32°方向线,
OB表示南偏东43°方向线,则∠AOB等于多少度?
4、如图5,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出客轮B、货轮C和海岛D方向的射线.
【设计意图】根据学生的情况,我主要采取自主探究、小组交流的方式学习认识方位角,引导学生运用所学知识确定物体的大体方位,贴近学生生活的问题,很好的体现了数学的应用价值,调动学生学习兴趣的同时,使学生积极参与学习活动。
教师在这一环节中参与到学生的讨论交流中,及时引导,归纳总结出方位角的画法及应用,培养学生的合作交流能力的同时,也让学生亲自体验了知识的产生过程,品尝到了学习的乐趣。
(四)学以致用
品尝成功(10分钟)
本着低起点、小台阶的原则,将练习分层次设置,以帮助学生实现从易到难、从会学到会用、从知识到能力的迁移,我设置了以下两个练习。
做一做——夯实基础
1、如图7,(1)射线OA表示________的方向;(2)OB表示______方向或________方向;(3)OC表示南_______方向.
2、如图8,下列说法错误的是(
)
A.
OA的方向是北偏西22°
B.
OB方向是西南方向
C.
OC的方向是南偏东60°
D.
OD的方向是北偏东60°
3、如图9,OA表示北偏东30°方向的一条射线,依照这条射线,画出表示下列方向的射线.
(1)南偏东25°;
(2)北偏西60°;
(3)东南方向.
想一想——发散思维
4、A看B的方向是北偏东21°,那么B看A的方向(
)
A:南偏东69°
B:南偏西69°
C:南偏东21°
D:南偏西21°
5、小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西
40°方向走了4米,到达点C,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离。
【设计意图】这些练习的设置,可以让学生多角度,全方位发挥其思维的深度和广度,拓宽学生的认知领域,培养学生的发散思维能力
(五)达标测试
(9分钟)
为了实现人人都学有价值的数学,不同层次学生都能得到发展,我设置了必做题和选做题,让学生品尝成功,树立信心。
必做题:(认真仔细,你一定有更大的收获!)
1、如图10,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于多少?
2、如图,OA表示北偏东32°方向线,
OB表示南偏东43°方向线,则∠AOB等于
3、在点O
北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是(
)
A:100°
B:70°
C:180°
D:140°
4、灯塔A在灯塔B的南偏东60°方向上,A、B相距30海里,轮船C在B的正南方向,在灯塔A的南偏西60°方向上,通过画图(用1个单位代表10海里)确定轮船C的位置,求∠BAC和∠ACB的度数,并求出轮船C与灯塔B的距离.
再攀新高峰:(选做题)
5、(1)如图6,xx中学2014年5月6日将举行运动会,一名服务的同学往返于百米起跑点A、终点B(A、B位于东西方向)及检录处C,他在A处看C点位于北偏东60°的方向上,在B点处看C点位于西北方向上(即北偏西45°),你能确定检录处C的位置么?
(2)检录处C在起点A的北偏东60°的方向上,那么起点A在检录处C的什么方向上呢?(
)
A.南偏东30°
B.南偏西30°
C.南偏东60°
D.南偏西60°
(3)如果测的AB的图上距离是4Cm,AC的图上距离是6Cm,那么,一个服务同学从A点跑到C点,在从C点跑回A点,他实际上跑了多少路程?
(学生独立完成,小组交流订正,独立完成整理到错题集上)
学后反思
1、我学会的(
知
识
、方
法)有:
。
2、注意点有
。
3、对自己想说的一句话是:
。
