人教版四年级下册数学三角形的内角和课件(22张)
文档属性
| 名称 | 人教版四年级下册数学三角形的内角和课件(22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 11:57:50 | ||
图片预览




文档简介
R·四年级下册
一、谈话激趣,设疑导入
1
2
3
∠1+∠2+∠3=?
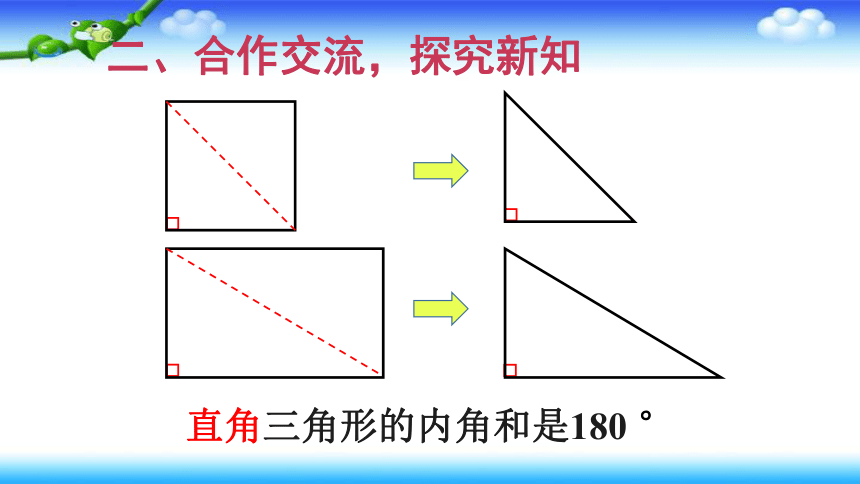
二、合作交流,探究新知
直角三角形的内角和是180 °
探究任意三角形的内角和
是不是任意三角形的内角和都是180°呢?
小组合作
请同学们小组合作,选一种喜欢的三角形,充分利用你们的学具进行验证,比一比,哪个组的方法多而且又富有新意。
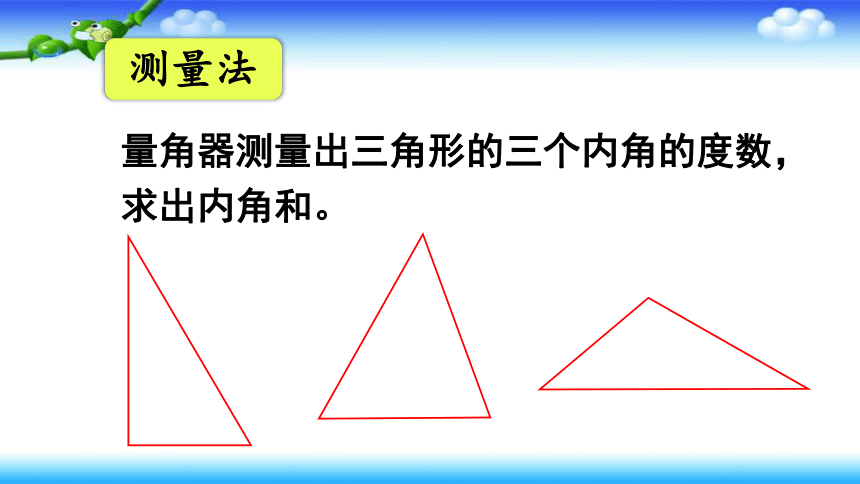
测量法
量角器测量出三角形的三个内角的度数,求出内角和。
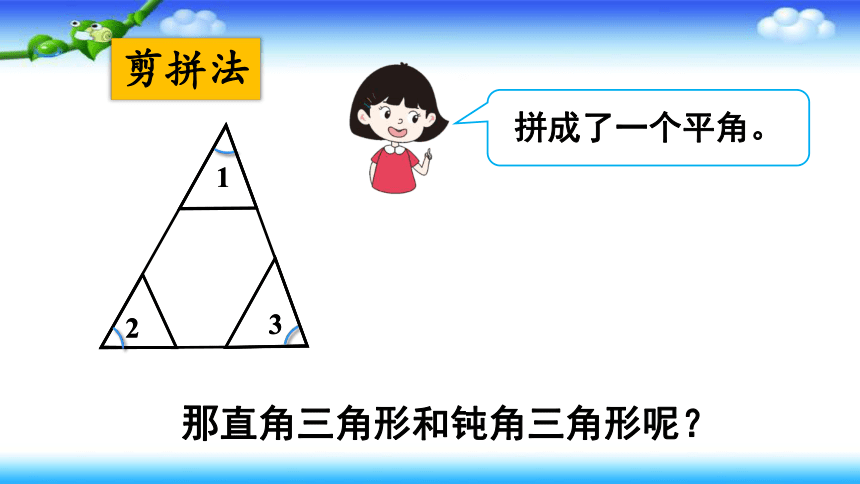
剪拼法
1
3
2
2
3
1
拼成了一个平角。
那直角三角形和钝角三角形呢?
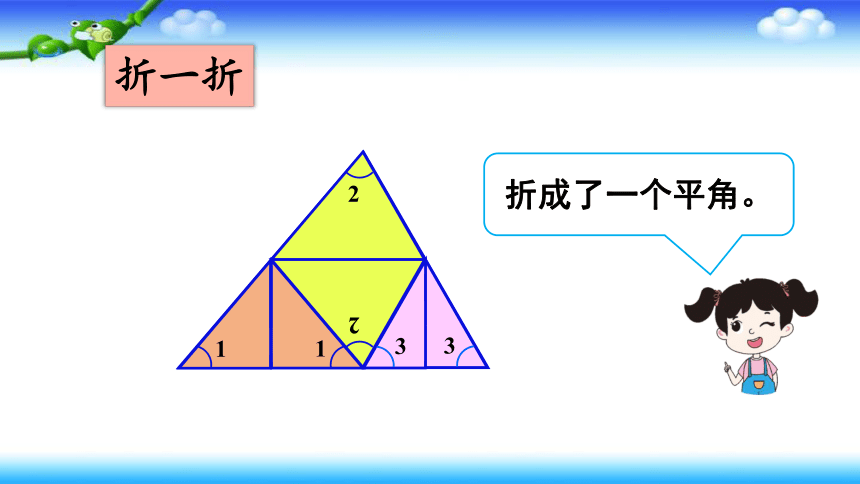
折一折
2
2
1
1
折成了一个平角。
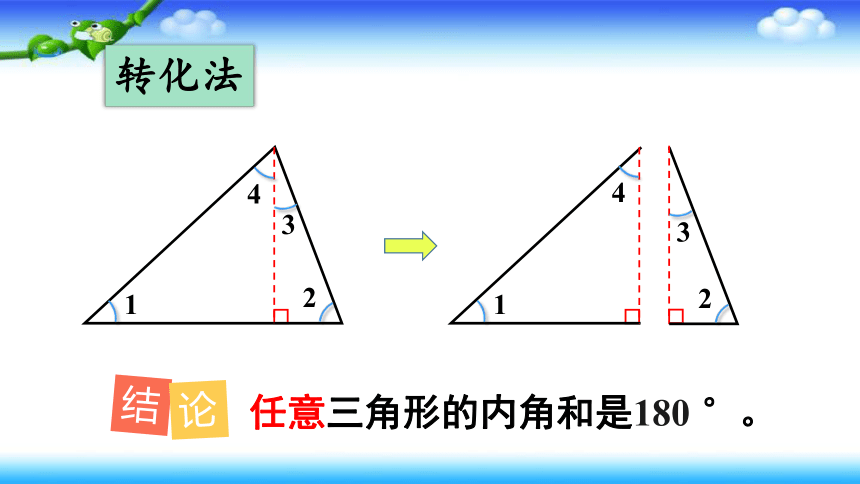
转化法
1
4
2
3
1
4
2
3
任意三角形的内角和是180 °。
结
论
阅读教科书 P67 例 6,厘清思路,大胆质疑。
1. 在右图中,∠1=140°,∠3=25°。求∠2 的度数。
∠1+∠2+∠3=180°
∠2=180°-∠1-∠2
=180°-140°-25°
=15°
三、巩固运用,解决问题
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
2.算出下面各个未知角的度数。
180°
3. 把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
每个角都是60°
底角是42°
另一个锐角是50°
4.求出三角形各个角的度数。
180°-(70°×2)=40°
答:它的顶角是 40°。
5.爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
在三角形中,一个是直角,另两个角可能各是多少度?
三角形的两条边分别是3cm和4cm,另一条边可能是多少厘米?
30°和60°
5cm
(1)
(2)
6.猜一猜。
任意三角形的内角和是180°。
四、课堂小结,深化认识
1.填空。
(1)三角形的内角和是( )。
(2)一个三角形中,一个角是70°,另一个角是40°,第三个角是( )°, 按边分,这是一个( )三角形。
?备选练习
180°
70
等腰
(3)直角三角形的两个锐角的和是( )°,等边三角形的三个内角都是( )°。
(4)等腰三角形的一个底角是50°,那么它的顶角是( )°。
(5)(2019·湖北武汉)一个三角形,如果它的两个内角的度数之和等于另一个内角的度数,那么这个三角形一定是( )三角形。
90
60
80
直角
2.求下面各三角形中未知角的度数。
(1)
(2)
(1)180°-(45°+60°)=75°
(2)180°-40°-105°=35°
(4)
(3)
(3)180°-(90°+52°)=38°
(4)180°-60°=120°
180°-(120°+40°)=20°
∠C=180°-25°-40°=115°
3.在三角形ABC 中,如果∠A =25°,∠B =40°,那么∠C 是多少度?
一、谈话激趣,设疑导入
1
2
3
∠1+∠2+∠3=?
二、合作交流,探究新知
直角三角形的内角和是180 °
探究任意三角形的内角和
是不是任意三角形的内角和都是180°呢?
小组合作
请同学们小组合作,选一种喜欢的三角形,充分利用你们的学具进行验证,比一比,哪个组的方法多而且又富有新意。
测量法
量角器测量出三角形的三个内角的度数,求出内角和。
剪拼法
1
3
2
2
3
1
拼成了一个平角。
那直角三角形和钝角三角形呢?
折一折
2
2
1
1
折成了一个平角。
转化法
1
4
2
3
1
4
2
3
任意三角形的内角和是180 °。
结
论
阅读教科书 P67 例 6,厘清思路,大胆质疑。
1. 在右图中,∠1=140°,∠3=25°。求∠2 的度数。
∠1+∠2+∠3=180°
∠2=180°-∠1-∠2
=180°-140°-25°
=15°
三、巩固运用,解决问题
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
2.算出下面各个未知角的度数。
180°
3. 把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
每个角都是60°
底角是42°
另一个锐角是50°
4.求出三角形各个角的度数。
180°-(70°×2)=40°
答:它的顶角是 40°。
5.爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
在三角形中,一个是直角,另两个角可能各是多少度?
三角形的两条边分别是3cm和4cm,另一条边可能是多少厘米?
30°和60°
5cm
(1)
(2)
6.猜一猜。
任意三角形的内角和是180°。
四、课堂小结,深化认识
1.填空。
(1)三角形的内角和是( )。
(2)一个三角形中,一个角是70°,另一个角是40°,第三个角是( )°, 按边分,这是一个( )三角形。
?备选练习
180°
70
等腰
(3)直角三角形的两个锐角的和是( )°,等边三角形的三个内角都是( )°。
(4)等腰三角形的一个底角是50°,那么它的顶角是( )°。
(5)(2019·湖北武汉)一个三角形,如果它的两个内角的度数之和等于另一个内角的度数,那么这个三角形一定是( )三角形。
90
60
80
直角
2.求下面各三角形中未知角的度数。
(1)
(2)
(1)180°-(45°+60°)=75°
(2)180°-40°-105°=35°
(4)
(3)
(3)180°-(90°+52°)=38°
(4)180°-60°=120°
180°-(120°+40°)=20°
∠C=180°-25°-40°=115°
3.在三角形ABC 中,如果∠A =25°,∠B =40°,那么∠C 是多少度?
