人教版四年级下册数学多边形的内角和课件(19张)
文档属性
| 名称 | 人教版四年级下册数学多边形的内角和课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 12:02:09 | ||
图片预览




文档简介
R·四年级下册
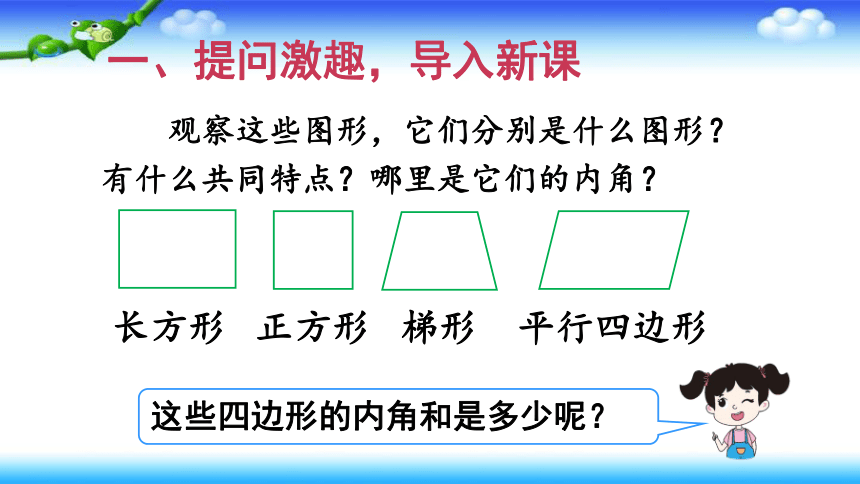
一、提问激趣,导入新课
观察这些图形,它们分别是什么图形?有什么共同特点?哪里是它们的内角?
长方形
正方形
平行四边形
梯形
这些四边形的内角和是多少呢?
四边形的内角和是多少度?
阅读与理解
四边形可以分成几种图形?
长方形
正方形
平行四边形
梯形
普通四边形
这些图形的内角和是不是一样的呢?
二、合作交流,探索四边形的内角和
分析与操作
长方形和正方形的 4 个角都是直角,它们的内角和是 360°。
90?×4=360°
小组合作:探究平行四边形、梯形或不规则四边形的内角和是多少度?
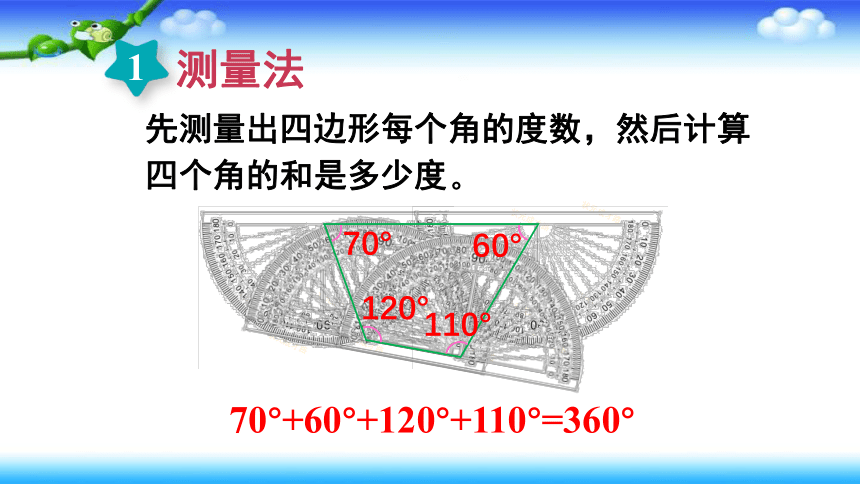
先测量出四边形每个角的度数,然后计算四个角的和是多少度。
1
测量法
70°
60°
120°
110°
70°+60°+120°+110°=360°
1
1
2
2
4
3
3
4
2
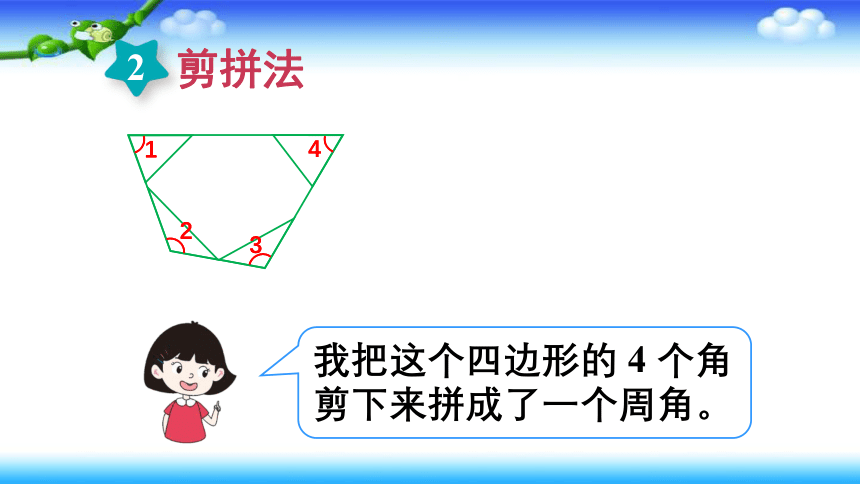
剪拼法
我把这个四边形的 4 个角剪下来拼成了一个周角。
3
分割法
我把这个四边形分成了 2 个三角形。
一个三角形的内角和是180°,两个相加为360°。
结
论
四边形的内角和是_______。
360°
回顾与反思
我们大家共同证明了所有四边形的内角和都是360°。结合前面所学的知识,你们想一想,最好最直接的办法是怎样的呢?
分割法,看分成了几个三角形,就有几个180°。
一个五边形可以分成三个三角形,它的内角和就有 3 个 180°。
3 × 180°= 540°
三、拓展延伸,加深理解
1.探究五边形的内角和。
2.你能想办法求出右边这个多边形的内角和吗?
你是怎么想的呢?
提示:将六边形分成了三角形再计算!
我把这个六边形分成了 4 个三角形,180?×4=720?。
我把这个六边形分成了 6 个三角形,把 6 个三角形的内角加起来再减去中间的一个周角,180?×6-360?=720?
6
7
2
3
180?×4
180?×5
3.画一画,算一算,你发现了什么?
发现
每个多边形都可以分成(n-2)个三角形,n边形的内角和=180?×(n-2)。
n 是多边形的边数。
4.连一连。
5.下面图形中各有多少个三角形?有什么规律?
1
1+2=3
1+2+3=6
1+2+3+4=10
第 n 幅图三角形个数为1+2+3+…+(n-1)+n,n 为大三角形被分成的基础三角形个数。
多边形的内角和
四边形的内角和是 360°。
n 边形的内角和= 180°×(n-2)。
四、课堂小结,交流收获
填表,发现规律。
?备选练习
我发现:n(n≥3)边形的内角和=____________
3
1
180°
4
2
360°
5
3
540°
6
4
720°
180°×(n-2)
一、提问激趣,导入新课
观察这些图形,它们分别是什么图形?有什么共同特点?哪里是它们的内角?
长方形
正方形
平行四边形
梯形
这些四边形的内角和是多少呢?
四边形的内角和是多少度?
阅读与理解
四边形可以分成几种图形?
长方形
正方形
平行四边形
梯形
普通四边形
这些图形的内角和是不是一样的呢?
二、合作交流,探索四边形的内角和
分析与操作
长方形和正方形的 4 个角都是直角,它们的内角和是 360°。
90?×4=360°
小组合作:探究平行四边形、梯形或不规则四边形的内角和是多少度?
先测量出四边形每个角的度数,然后计算四个角的和是多少度。
1
测量法
70°
60°
120°
110°
70°+60°+120°+110°=360°
1
1
2
2
4
3
3
4
2
剪拼法
我把这个四边形的 4 个角剪下来拼成了一个周角。
3
分割法
我把这个四边形分成了 2 个三角形。
一个三角形的内角和是180°,两个相加为360°。
结
论
四边形的内角和是_______。
360°
回顾与反思
我们大家共同证明了所有四边形的内角和都是360°。结合前面所学的知识,你们想一想,最好最直接的办法是怎样的呢?
分割法,看分成了几个三角形,就有几个180°。
一个五边形可以分成三个三角形,它的内角和就有 3 个 180°。
3 × 180°= 540°
三、拓展延伸,加深理解
1.探究五边形的内角和。
2.你能想办法求出右边这个多边形的内角和吗?
你是怎么想的呢?
提示:将六边形分成了三角形再计算!
我把这个六边形分成了 4 个三角形,180?×4=720?。
我把这个六边形分成了 6 个三角形,把 6 个三角形的内角加起来再减去中间的一个周角,180?×6-360?=720?
6
7
2
3
180?×4
180?×5
3.画一画,算一算,你发现了什么?
发现
每个多边形都可以分成(n-2)个三角形,n边形的内角和=180?×(n-2)。
n 是多边形的边数。
4.连一连。
5.下面图形中各有多少个三角形?有什么规律?
1
1+2=3
1+2+3=6
1+2+3+4=10
第 n 幅图三角形个数为1+2+3+…+(n-1)+n,n 为大三角形被分成的基础三角形个数。
多边形的内角和
四边形的内角和是 360°。
n 边形的内角和= 180°×(n-2)。
四、课堂小结,交流收获
填表,发现规律。
?备选练习
我发现:n(n≥3)边形的内角和=____________
3
1
180°
4
2
360°
5
3
540°
6
4
720°
180°×(n-2)
