五年级下册数学教案 5.1 可能性 沪教版
文档属性
| 名称 | 五年级下册数学教案 5.1 可能性 沪教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 07:21:37 | ||
图片预览


文档简介
可能性的大小
教材内容:可能性的大小(义务教育课本五年级第二学期P72-73)。
教学目标:
1、经历实验的具体过程,知道不确定现象发生的可能性是有大小的。
2、初步了解一些简单不确定现象发生可能性的大小,并能作出简单判断和适当的解释。
3、通过积极参与猜想、实验、验证、分析的过程,提高思维、实践能力。
教学重点:
知道不确定现象发生的可能性是有大小的,知道哪种不确定现象发生的可能性大。
教学难点:
利用事件发生的可能性的知识对实际问题进行判断和预测。
教学过程:
一、巩固旧知,引入新知
1、可能性相同事件
出示十个黄球,球上分别标上1-10的数字,每次从口袋里摸出一个球。
提问:摸到数字1-10的可能性相同吗?为什么?
小结:袋子中都是黄球,摸出每个球的可能性相同。
2.8个黄球、2个白球等
如果把握把其中的三个黄球换成白球,请问每次从袋中摸出每一个球的可能性相同吗?
(每次摸出一个球的可能性相同。)
那摸出的白球可能性大,还是黄球可能性大?
为什么呢?
3、导入:可能性的大小是不是和数量有关呢?今天我们就要研究这个问题。
[板书:可能性的大小]
二、实验探究,验证猜测
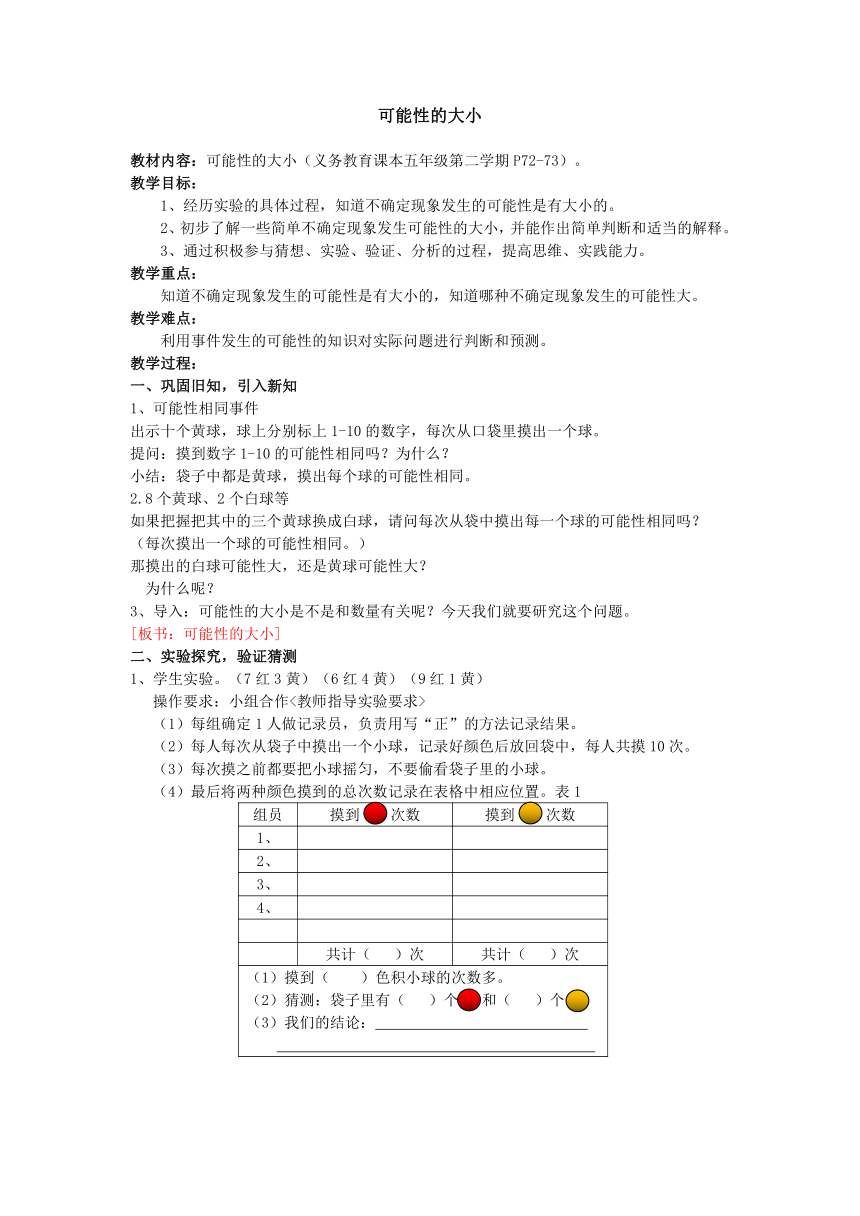
1、学生实验。(7红3黄)(6红4黄)(9红1黄)
操作要求:小组合作<教师指导实验要求>
(1)每组确定1人做记录员,负责用写“正”的方法记录结果。
(2)每人每次从袋子中摸出一个小球,记录好颜色后放回袋中,每人共摸10次。
(3)每次摸之前都要把小球摇匀,不要偷看袋子里的小球。
(4)最后将两种颜色摸到的总次数记录在表格中相应位置。表1
组员
摸到 次数
摸到 次数
1、
2、
3、
4、
共计( )次
共计( )次
(1)摸到( )色积小球的次数多。
(2)猜测:袋子里有( )个 和( )个 。
(3)我们的结论:
2、汇报交流实验结果。
导语:每个小组已经完成了实验,说一说你们组实验的结果。
(1)师:你们猜测一下你们的袋子中可能有几个红色和几个黄色的?为什么?
生:根据自己小组的实验结果猜测两种颜色小球的数量。
(2)师:打开袋子验证一下你们的猜测是否正确。
3、总结规律。
师:通过这个实验,你们有了什么结论?
生:红球的数量比黄球多,摸出红球的可能性大。红球的数量比黄球数量少,摸出红球的可能性小。
红球的数量比黄球多的越多,摸出红球的可能性就越大。
摸的次数越多,摸到红色/黄色球的可能性就越大。
小结:可能性的大小和数量的多少有关(板书)。
数量多,可能性大;
数量少,可能性小。
(当实验次数越多,可能性的大小会越明显。)
4、深化结论。
(1)师:如果从你们小组的袋子中继续再摸出一个球,只摸一个,可能会摸到什么颜色的球?
生:红色;黄色;可能是红色也可能是黄色。
(2)师:请每个小组派一个代表继续摸一个验证你们的想法。
师:明明你们小组是摸出红球(黄球)的可能性大,为什么摸到的却是黄球(红球)呢?
生:摸到的可能性小并不代表不会摸到,每次摸的时候既有可能是黄色的,又有可能是红色的。
小结:可能性的大小不能确定单次的结果。[板书:可能性大小不能确定单次的结果]
(3)师:能不能使摸到的红球和黄球的可能性一样大?袋子应该里怎么放?为什么?
生:放入的红色和黄色球数量相同。
(4)师:经过刚才实验和讨论,谁能说一说你们得到哪些结论?
生:可能性大小与物体数量多少是密切相关的,可能性的大小并不能确定单次的结果。
三、练习巩固,深化认识
(一)导语:我们在“猜测——验证”的过程中做出了可能性大小的判断,现在你们能直接根据数量来判定可能性大小吗?
(1)连一连。
每次摸一个球,在每个口袋里都摸30次,结果会怎样?你能用线连一连吗?
2.这些方法公平吗?
(1)抛硬币,正面朝上小胖先来,反面朝上小巧先来。
(2)玩剪刀石头布,谁获胜谁先来。
(3)掷点数块,大于3小胖先来,小于3小巧先来。
3.一只小鸟受伤后,落在右图的哪一块可能性最大( )
A.① B.② C.③ D.一样大
②
①
③
4.小猴在1号箱里一定能摸出( ),不可能摸到( )和( )。在2号箱里摸到苹果的可能性( ),摸到梨的可能性( ),一定摸不到( )。
5个桃
2个梨5个苹果
1
2
思考题:如果我的超市经理。
3124200259080“6.18”购物节这天凡在商场当日消费满1888元的顾客,可凭收银条参加转盘抽奖活动。奖品如下:
一等奖(红色):苹果笔记本 一台
二等奖(蓝色):iphone X 一部
三等奖(黄色):点读机 一台
请你为这个转盘涂色。
小结:我们应用所学的知识,解决了抽奖转盘的设计问题,知道了涂色面大,转到的可能性就大,涂色面小,转到的可能性就小。<涂色面大小对应数量的多少>
补充:谁猜对的可能性大?
我是小淘气,我要参加足球赛,我的号码是1~10中的一个数 。
我猜是单数。
我猜是3的倍数。
我猜是大于6的数。
我猜是不大于6的数。
小胖猜是单数。(5个)
小巧猜是3的倍数。(3个)
小亚猜是大于6的数。(4个)
小丁丁猜是不大于6的数。(6个)
四、渗透数学知识,拓展认识
导语:对于不确定事件发生的可能性是有大小的,在数学上就把这种可能性的大小叫做概率。概率是在怎么发展而来的?我们一起来看看。
第一个系统地推算概率的人是16世纪的卡尔达诺。卡尔达诺的数学著作中有很多给赌徒的建议。这些建议都写成短文。例如:《谁,在什么时候,应该赌博?》、《为什么亚里斯多德谴责赌博?》、《那些教别人赌博的人是否也擅长赌博呢?》等。
然而,首次提出系统研究概率的是在帕斯卡和费马来往的一系列信件中。这些通信最初是由帕斯卡提出的,他想找费马请教几个关于由Chevvalier de Mere提出的问题。Chevvalier de Mere是一知名作家,路易十四宫廷的显要,也是一名狂热的赌徒。问题主要是两个:掷骰子问题和比赛奖金分配问题。
五、课堂总结
这节课我们学会了什么?
六.板书设计
可能性的大小和数量的多少有关(板书)。
数量多,可能性大;
数量少,可能性小。
[板书:可能性大小不能确定单次的结果
教材内容:可能性的大小(义务教育课本五年级第二学期P72-73)。
教学目标:
1、经历实验的具体过程,知道不确定现象发生的可能性是有大小的。
2、初步了解一些简单不确定现象发生可能性的大小,并能作出简单判断和适当的解释。
3、通过积极参与猜想、实验、验证、分析的过程,提高思维、实践能力。
教学重点:
知道不确定现象发生的可能性是有大小的,知道哪种不确定现象发生的可能性大。
教学难点:
利用事件发生的可能性的知识对实际问题进行判断和预测。
教学过程:
一、巩固旧知,引入新知
1、可能性相同事件
出示十个黄球,球上分别标上1-10的数字,每次从口袋里摸出一个球。
提问:摸到数字1-10的可能性相同吗?为什么?
小结:袋子中都是黄球,摸出每个球的可能性相同。
2.8个黄球、2个白球等
如果把握把其中的三个黄球换成白球,请问每次从袋中摸出每一个球的可能性相同吗?
(每次摸出一个球的可能性相同。)
那摸出的白球可能性大,还是黄球可能性大?
为什么呢?
3、导入:可能性的大小是不是和数量有关呢?今天我们就要研究这个问题。
[板书:可能性的大小]
二、实验探究,验证猜测
1、学生实验。(7红3黄)(6红4黄)(9红1黄)
操作要求:小组合作<教师指导实验要求>
(1)每组确定1人做记录员,负责用写“正”的方法记录结果。
(2)每人每次从袋子中摸出一个小球,记录好颜色后放回袋中,每人共摸10次。
(3)每次摸之前都要把小球摇匀,不要偷看袋子里的小球。
(4)最后将两种颜色摸到的总次数记录在表格中相应位置。表1
组员
摸到 次数
摸到 次数
1、
2、
3、
4、
共计( )次
共计( )次
(1)摸到( )色积小球的次数多。
(2)猜测:袋子里有( )个 和( )个 。
(3)我们的结论:
2、汇报交流实验结果。
导语:每个小组已经完成了实验,说一说你们组实验的结果。
(1)师:你们猜测一下你们的袋子中可能有几个红色和几个黄色的?为什么?
生:根据自己小组的实验结果猜测两种颜色小球的数量。
(2)师:打开袋子验证一下你们的猜测是否正确。
3、总结规律。
师:通过这个实验,你们有了什么结论?
生:红球的数量比黄球多,摸出红球的可能性大。红球的数量比黄球数量少,摸出红球的可能性小。
红球的数量比黄球多的越多,摸出红球的可能性就越大。
摸的次数越多,摸到红色/黄色球的可能性就越大。
小结:可能性的大小和数量的多少有关(板书)。
数量多,可能性大;
数量少,可能性小。
(当实验次数越多,可能性的大小会越明显。)
4、深化结论。
(1)师:如果从你们小组的袋子中继续再摸出一个球,只摸一个,可能会摸到什么颜色的球?
生:红色;黄色;可能是红色也可能是黄色。
(2)师:请每个小组派一个代表继续摸一个验证你们的想法。
师:明明你们小组是摸出红球(黄球)的可能性大,为什么摸到的却是黄球(红球)呢?
生:摸到的可能性小并不代表不会摸到,每次摸的时候既有可能是黄色的,又有可能是红色的。
小结:可能性的大小不能确定单次的结果。[板书:可能性大小不能确定单次的结果]
(3)师:能不能使摸到的红球和黄球的可能性一样大?袋子应该里怎么放?为什么?
生:放入的红色和黄色球数量相同。
(4)师:经过刚才实验和讨论,谁能说一说你们得到哪些结论?
生:可能性大小与物体数量多少是密切相关的,可能性的大小并不能确定单次的结果。
三、练习巩固,深化认识
(一)导语:我们在“猜测——验证”的过程中做出了可能性大小的判断,现在你们能直接根据数量来判定可能性大小吗?
(1)连一连。
每次摸一个球,在每个口袋里都摸30次,结果会怎样?你能用线连一连吗?
2.这些方法公平吗?
(1)抛硬币,正面朝上小胖先来,反面朝上小巧先来。
(2)玩剪刀石头布,谁获胜谁先来。
(3)掷点数块,大于3小胖先来,小于3小巧先来。
3.一只小鸟受伤后,落在右图的哪一块可能性最大( )
A.① B.② C.③ D.一样大
②
①
③
4.小猴在1号箱里一定能摸出( ),不可能摸到( )和( )。在2号箱里摸到苹果的可能性( ),摸到梨的可能性( ),一定摸不到( )。
5个桃
2个梨5个苹果
1
2
思考题:如果我的超市经理。
3124200259080“6.18”购物节这天凡在商场当日消费满1888元的顾客,可凭收银条参加转盘抽奖活动。奖品如下:
一等奖(红色):苹果笔记本 一台
二等奖(蓝色):iphone X 一部
三等奖(黄色):点读机 一台
请你为这个转盘涂色。
小结:我们应用所学的知识,解决了抽奖转盘的设计问题,知道了涂色面大,转到的可能性就大,涂色面小,转到的可能性就小。<涂色面大小对应数量的多少>
补充:谁猜对的可能性大?
我是小淘气,我要参加足球赛,我的号码是1~10中的一个数 。
我猜是单数。
我猜是3的倍数。
我猜是大于6的数。
我猜是不大于6的数。
小胖猜是单数。(5个)
小巧猜是3的倍数。(3个)
小亚猜是大于6的数。(4个)
小丁丁猜是不大于6的数。(6个)
四、渗透数学知识,拓展认识
导语:对于不确定事件发生的可能性是有大小的,在数学上就把这种可能性的大小叫做概率。概率是在怎么发展而来的?我们一起来看看。
第一个系统地推算概率的人是16世纪的卡尔达诺。卡尔达诺的数学著作中有很多给赌徒的建议。这些建议都写成短文。例如:《谁,在什么时候,应该赌博?》、《为什么亚里斯多德谴责赌博?》、《那些教别人赌博的人是否也擅长赌博呢?》等。
然而,首次提出系统研究概率的是在帕斯卡和费马来往的一系列信件中。这些通信最初是由帕斯卡提出的,他想找费马请教几个关于由Chevvalier de Mere提出的问题。Chevvalier de Mere是一知名作家,路易十四宫廷的显要,也是一名狂热的赌徒。问题主要是两个:掷骰子问题和比赛奖金分配问题。
五、课堂总结
这节课我们学会了什么?
六.板书设计
可能性的大小和数量的多少有关(板书)。
数量多,可能性大;
数量少,可能性小。
[板书:可能性大小不能确定单次的结果
