2011年秋学期高二数学(理)期中检测(含完整答案)
文档属性
| 名称 | 2011年秋学期高二数学(理)期中检测(含完整答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 189.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-03 00:00:00 | ||
图片预览



文档简介
2011年秋学期高二数学(理)期中检测
一、填空题(本大题共14道小题,每题5分,共70分,请将答案写在答题纸指定横线上)
1.数列的通项公式为,(为常数)是该数列为等差数列的 条件(填“充分不必要”,“必要不充分”, “充要”, “既不充分也不必要”中的一个).
2.等差数列中,若, ,则 .
3.等比数列{an}中,an>0,且,则log2a2+log2a4+log2a8+log2a10=___________.
4.数列的通项公式为,则该数列的前100项和为___________.
5.等差数列中,,,则其前n项和的最小值为___________.
6.设正项等比数列的前n项和为,且+=,则数列的公比为 .
7.若成等差数列,成等比数列,则 .
(结果用区间形式表示)
8.已知关于x不等式的解集为,则的取值范围为___________.
9.已知{}是公差不为0的等差数列,不等式的解集是,则= .
10.设a>0,b>0,称为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E.则图中线段OD的长度是a,b的算术平均数,线段CD的长度是a,b的几何平均数,那么a,b的调和平均数是线段 的长度.
11.等差数列中,是其前n项和,,,则的值为
___________.
12.设满足约束条件,若目标函数的最大值为12,则的最小值为___________.
13.设等差数列的首项及公差均是正整数,前项和为,且,,,则= .
14.设数列{an}的前n项和为Sn.若{Sn}是首项及公比都为2的等比数列,则数列{an3}的前
n项和等于 .
二、解答题 (本大题共6道小题,共90分,请将答案写在答题纸指定区域内)
15.(本小题满分14分)
一个正方形被等分成九个相等的小正方形,将中间的一个正方形挖掉如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖掉,得图(2);如此继续下去……,
(1)第三个图中共挖掉多少个正方形;
(2)设原正方形边长为1,则第n个图中被挖掉的所有小正方形的面积和为多少?
(1) (2)
16.(本小题满分14分)
已知是等差数列,公差,前项和为且满足.
对于数列,其通项公式,如果数列也是等差数列。
(1)求非零常数C的值; (2)试求函数()的最大值.
17.(本小题满分14分)
已知二次函数的二次项系数为,且不等式的解集为(1,3).
(1)若方程有两个相等的根,求的解析式;
(2)若的最大值为正数,求的取值范围.
18.(本小题满分16分)
设数列的各项均为正数,它的前n项和为,点在函数的图象上,数列的通项公式为,其前项和为。
⑴求 (2)求证:
19.(本小题满分16分) 已知函数
(1)试求的值;
(2)若数列 ,求数列的通项公式;
(3)若数列满足,是数列前项的和,是否存在正实数,使不等式对于一切的恒成立?若存在指出的取值范围,并证明;若不存在说明理由.
20.(本小题满分16分)
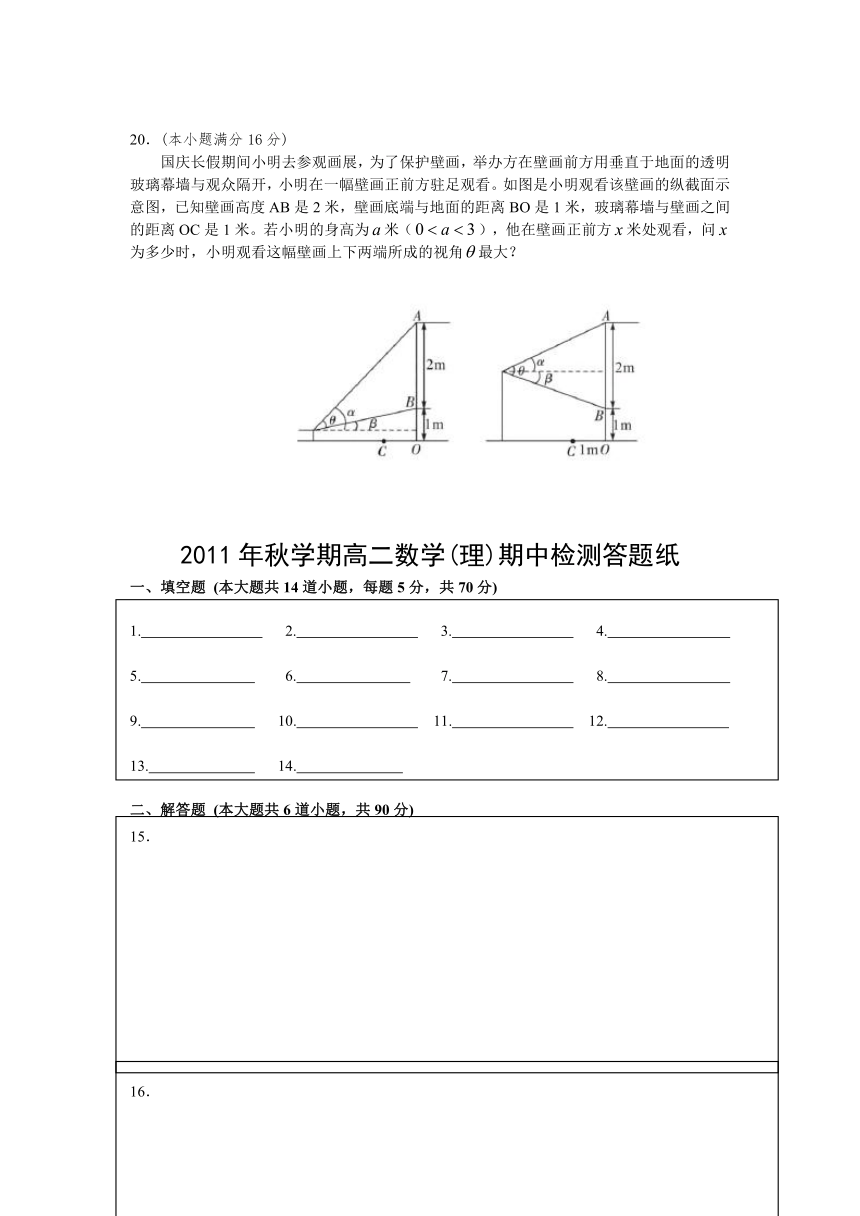
国庆长假期间小明去参观画展,为了保护壁画,举办方在壁画前方用垂直于地面的透明玻璃幕墙与观众隔开,小明在一幅壁画正前方驻足观看。如图是小明观看该壁画的纵截面示意图,已知壁画高度AB是2米,壁画底端与地面的距离BO是1米,玻璃幕墙与壁画之间的距离OC是1米。若小明的身高为米(),他在壁画正前方米处观看,问为多少时,小明观看这幅壁画上下两端所成的视角最大?
2011年秋学期高二数学(理)期中检测答题纸
一、填空题 (本大题共14道小题,每题5分,共70分)
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12.
13. 14.
二、解答题 (本大题共6道小题,共90分)
15.
16.
17.
18.
19.(本小题满分16分)
20.(本小题满分16分)
2011年秋学期高二数学(理)期中检测
一、填空题(本大题共14道小题,每题5分,共70分)
1.一个数列的通项公式,(都是常数)是该数列为等差数列的 条件(填充分不必要,必要不充分,充要,既不充分也不必要中的一个)
2.等差数列中,若, ,则 .
3.等比数列{an}中,an>0,且a3·a6·a9=4,则log2a2+log2a4+log2a8+log2a10=______
4.数列的通项公式为,则前100项和为___________
5.等差数列中,,则前n项和的最小值为_______ 4 ____
6.设正项等比数列的前n项和为,且+=,则数列的公比 .
7.已知a>0,b>0,a+b=2,则y=的最小值是________
8.已知关于x不等式kx2-2kx+6<0的解集为,求k的取值范围.[0,6]
9.已知{}是公差不为0的等差数列,不等式的解集是,则 .
10.设a>0,b>0,称为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
【答案】CD DE
11.等差数列中,是其前n项和,,,则的值为_____.
12.设满足约束条件若目标函数的最大值为12,则的最小值为
答案 4
13.设等差数列的首项及公差均是正整数,前项和为,且,,,则= 4020 .
14.设数列{an}的前n项和为Sn.若{Sn}是首项及公比都为2的等比数列,则数列{an3}的前
n项和等于 ▲ .
二、解答题(本大题共6道小题,共90分)
15.(本小题满分14分)
一个正方形被等分成九个相等的小正方形,将中间的一个正方形挖掉如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖掉,得图(2);如此继续下去……,
(1)第三个图中共挖掉多少个正方形;
(2)设原正方形边长为1,则第n个图中被挖掉的所有小正方形的面积和为多少?
16.(本小题满分14分)
已知等差数列,其公差,前项和为且满足.
数列,它的通项公式,如果数列也是等差数列。
(1)求非零常数C的值; (2)试求函数的最大值.
17.(本小题满分14分)
设数列的各项均为正数,它的前n项和为,点在函数的图象上,数列的前项和为,且(n=1,2,3…)
⑴求与 (2)记,求满足的最大正整数.
⑴n=1,a1=2 …(1)
Sn= ,n≥2,Sn-1= …(2)
Sn Sn-1=an= 整理得 …
解:(1)∵ ∴ 当时,
即 ∵ ∴ 即数列是等比数列
∵ ∴ 即 ∴
∵ 点在直线上 ∴ ∴
即数列是等差数列,又 ∴
(2) ①
∴ ②
①-②得
即 ∴
∵ 即 于是
又由于当时,, 当时,
故满足条件最大的正整数n为4
19.(本小题满分16分)
已知函数满足.
(1)求的值;
(2)若数列 ,求数列的通项公式;
(3)若数列满足,是数列前项的和,是否存在正实数,使不等式对于一切的恒成立?若存在指出的取值范围,并证明;若不存在说明理由.
(1)令,,……2分
令, ……5分
(2)∵ ①
∴ ②
由(Ⅰ),知
∴①+②,得 …… 10分
(3)∵ ,∴
∴, ①
, ②
①-②得
即 …… 12分
要使得不等式恒成立,即对于一切的恒成立,
设
当时,由于对称轴直线,且 ,而函数在 是增函数,∴不等式恒成立
即当实数大于时,不等式对于一切的恒成立 ……16分
20.(本小题满分16分)
一、填空题(本大题共14道小题,每题5分,共70分,请将答案写在答题纸指定横线上)
1.数列的通项公式为,(为常数)是该数列为等差数列的 条件(填“充分不必要”,“必要不充分”, “充要”, “既不充分也不必要”中的一个).
2.等差数列中,若, ,则 .
3.等比数列{an}中,an>0,且,则log2a2+log2a4+log2a8+log2a10=___________.
4.数列的通项公式为,则该数列的前100项和为___________.
5.等差数列中,,,则其前n项和的最小值为___________.
6.设正项等比数列的前n项和为,且+=,则数列的公比为 .
7.若成等差数列,成等比数列,则 .
(结果用区间形式表示)
8.已知关于x不等式的解集为,则的取值范围为___________.
9.已知{}是公差不为0的等差数列,不等式的解集是,则= .
10.设a>0,b>0,称为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E.则图中线段OD的长度是a,b的算术平均数,线段CD的长度是a,b的几何平均数,那么a,b的调和平均数是线段 的长度.
11.等差数列中,是其前n项和,,,则的值为
___________.
12.设满足约束条件,若目标函数的最大值为12,则的最小值为___________.
13.设等差数列的首项及公差均是正整数,前项和为,且,,,则= .
14.设数列{an}的前n项和为Sn.若{Sn}是首项及公比都为2的等比数列,则数列{an3}的前
n项和等于 .
二、解答题 (本大题共6道小题,共90分,请将答案写在答题纸指定区域内)
15.(本小题满分14分)
一个正方形被等分成九个相等的小正方形,将中间的一个正方形挖掉如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖掉,得图(2);如此继续下去……,
(1)第三个图中共挖掉多少个正方形;
(2)设原正方形边长为1,则第n个图中被挖掉的所有小正方形的面积和为多少?
(1) (2)
16.(本小题满分14分)
已知是等差数列,公差,前项和为且满足.
对于数列,其通项公式,如果数列也是等差数列。
(1)求非零常数C的值; (2)试求函数()的最大值.
17.(本小题满分14分)
已知二次函数的二次项系数为,且不等式的解集为(1,3).
(1)若方程有两个相等的根,求的解析式;
(2)若的最大值为正数,求的取值范围.
18.(本小题满分16分)
设数列的各项均为正数,它的前n项和为,点在函数的图象上,数列的通项公式为,其前项和为。
⑴求 (2)求证:
19.(本小题满分16分) 已知函数
(1)试求的值;
(2)若数列 ,求数列的通项公式;
(3)若数列满足,是数列前项的和,是否存在正实数,使不等式对于一切的恒成立?若存在指出的取值范围,并证明;若不存在说明理由.
20.(本小题满分16分)
国庆长假期间小明去参观画展,为了保护壁画,举办方在壁画前方用垂直于地面的透明玻璃幕墙与观众隔开,小明在一幅壁画正前方驻足观看。如图是小明观看该壁画的纵截面示意图,已知壁画高度AB是2米,壁画底端与地面的距离BO是1米,玻璃幕墙与壁画之间的距离OC是1米。若小明的身高为米(),他在壁画正前方米处观看,问为多少时,小明观看这幅壁画上下两端所成的视角最大?
2011年秋学期高二数学(理)期中检测答题纸
一、填空题 (本大题共14道小题,每题5分,共70分)
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12.
13. 14.
二、解答题 (本大题共6道小题,共90分)
15.
16.
17.
18.
19.(本小题满分16分)
20.(本小题满分16分)
2011年秋学期高二数学(理)期中检测
一、填空题(本大题共14道小题,每题5分,共70分)
1.一个数列的通项公式,(都是常数)是该数列为等差数列的 条件(填充分不必要,必要不充分,充要,既不充分也不必要中的一个)
2.等差数列中,若, ,则 .
3.等比数列{an}中,an>0,且a3·a6·a9=4,则log2a2+log2a4+log2a8+log2a10=______
4.数列的通项公式为,则前100项和为___________
5.等差数列中,,则前n项和的最小值为_______ 4 ____
6.设正项等比数列的前n项和为,且+=,则数列的公比 .
7.已知a>0,b>0,a+b=2,则y=的最小值是________
8.已知关于x不等式kx2-2kx+6<0的解集为,求k的取值范围.[0,6]
9.已知{}是公差不为0的等差数列,不等式的解集是,则 .
10.设a>0,b>0,称为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
【答案】CD DE
11.等差数列中,是其前n项和,,,则的值为_____.
12.设满足约束条件若目标函数的最大值为12,则的最小值为
答案 4
13.设等差数列的首项及公差均是正整数,前项和为,且,,,则= 4020 .
14.设数列{an}的前n项和为Sn.若{Sn}是首项及公比都为2的等比数列,则数列{an3}的前
n项和等于 ▲ .
二、解答题(本大题共6道小题,共90分)
15.(本小题满分14分)
一个正方形被等分成九个相等的小正方形,将中间的一个正方形挖掉如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖掉,得图(2);如此继续下去……,
(1)第三个图中共挖掉多少个正方形;
(2)设原正方形边长为1,则第n个图中被挖掉的所有小正方形的面积和为多少?
16.(本小题满分14分)
已知等差数列,其公差,前项和为且满足.
数列,它的通项公式,如果数列也是等差数列。
(1)求非零常数C的值; (2)试求函数的最大值.
17.(本小题满分14分)
设数列的各项均为正数,它的前n项和为,点在函数的图象上,数列的前项和为,且(n=1,2,3…)
⑴求与 (2)记,求满足的最大正整数.
⑴n=1,a1=2 …(1)
Sn= ,n≥2,Sn-1= …(2)
Sn Sn-1=an= 整理得 …
解:(1)∵ ∴ 当时,
即 ∵ ∴ 即数列是等比数列
∵ ∴ 即 ∴
∵ 点在直线上 ∴ ∴
即数列是等差数列,又 ∴
(2) ①
∴ ②
①-②得
即 ∴
∵ 即 于是
又由于当时,, 当时,
故满足条件最大的正整数n为4
19.(本小题满分16分)
已知函数满足.
(1)求的值;
(2)若数列 ,求数列的通项公式;
(3)若数列满足,是数列前项的和,是否存在正实数,使不等式对于一切的恒成立?若存在指出的取值范围,并证明;若不存在说明理由.
(1)令,,……2分
令, ……5分
(2)∵ ①
∴ ②
由(Ⅰ),知
∴①+②,得 …… 10分
(3)∵ ,∴
∴, ①
, ②
①-②得
即 …… 12分
要使得不等式恒成立,即对于一切的恒成立,
设
当时,由于对称轴直线,且 ,而函数在 是增函数,∴不等式恒成立
即当实数大于时,不等式对于一切的恒成立 ……16分
20.(本小题满分16分)
同课章节目录
