六年级下册数学课件-圆柱体积的探究 人教版(66张ppt)
文档属性
| 名称 | 六年级下册数学课件-圆柱体积的探究 人教版(66张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:36:44 | ||
图片预览




文档简介
(共66张PPT)
迁移
联系
推导
--《圆柱的体积》教学设计
背景分析
一
二
三
四
五
我的思考
教学目标
重点难点
教学流程
主要环节
六
说课内容
教学背景分析
课标要求
教材地位
知识内容
经历探究物体大小的过程,掌握转化中的基本关系。
最后一个内容,第一次学习含有曲面的几何体的体积。
理解公式的推导过程,会利用公式计算圆柱的体积。
1
教材的地位和作用
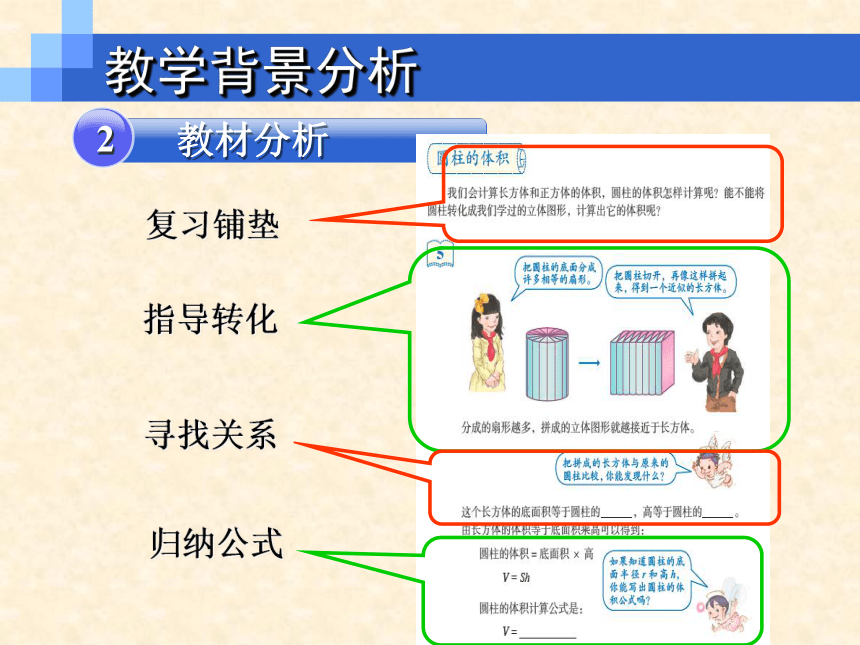
教学背景分析
2
教材分析
复习铺垫
指导转化
寻找关系
归纳公式
圆柱
体积
策略储备
知识储备
教学背景分析
3
学习的基础
什么是圆柱的体积?
怎么计算长方体的体积?
圆能转化成什么图形?
转化的意识
转化的方向
优势:知道圆怎样转化成近似的长方形,
能说出体积概念,
会利用公式求长方体、正方体的体积。
不足:
学生的立体空间观念还不是完全成熟,形体之间的转化还有一定的困难。
教学背景分析
4
学生情况分析
我的思考
学生有必要操作切割好的学具吗?
怎样的设计有利于学生理解?
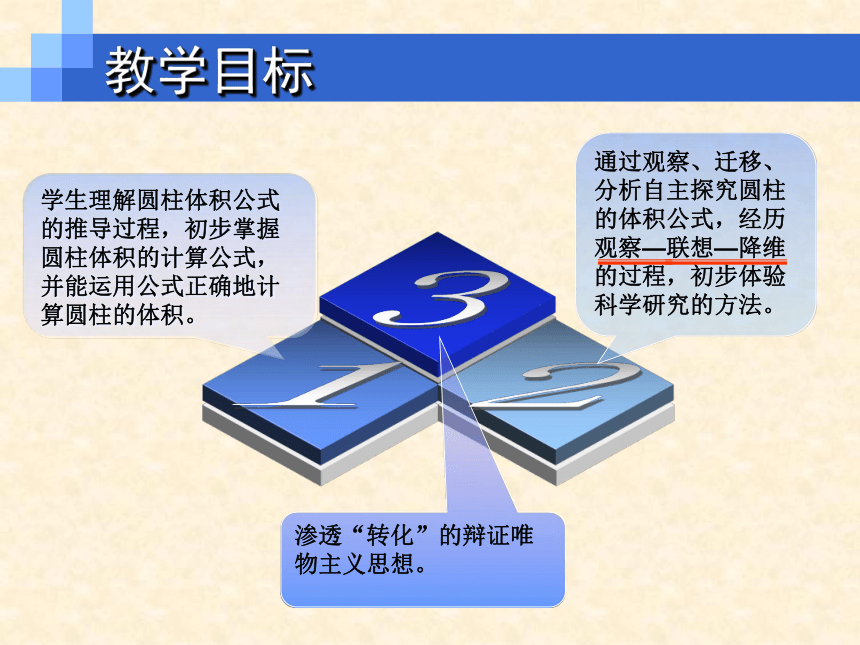
教学目标
学生理解圆柱体积公式的推导过程,初步掌握圆柱体积的计算公式,并能运用公式正确地计算圆柱的体积。
渗透“转化”的辩证唯物主义思想。
通过观察、迁移、分析自主探究圆柱的体积公式,经历观察—联想—降维的过程,初步体验科学研究的方法。
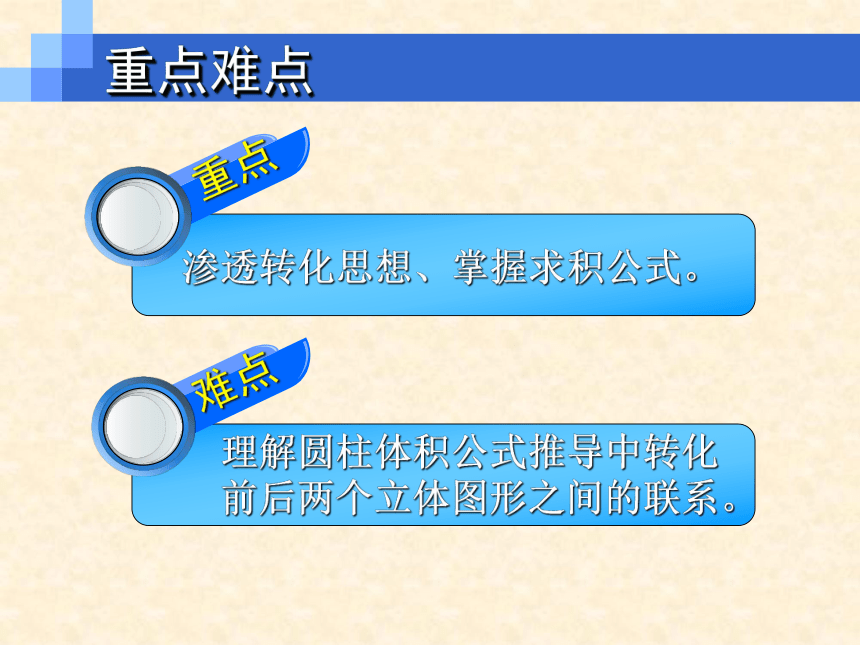
重点难点
理解圆柱体积公式推导中转化
前后两个立体图形之间的联系。
渗透转化思想、掌握求积公式。
重点
难点
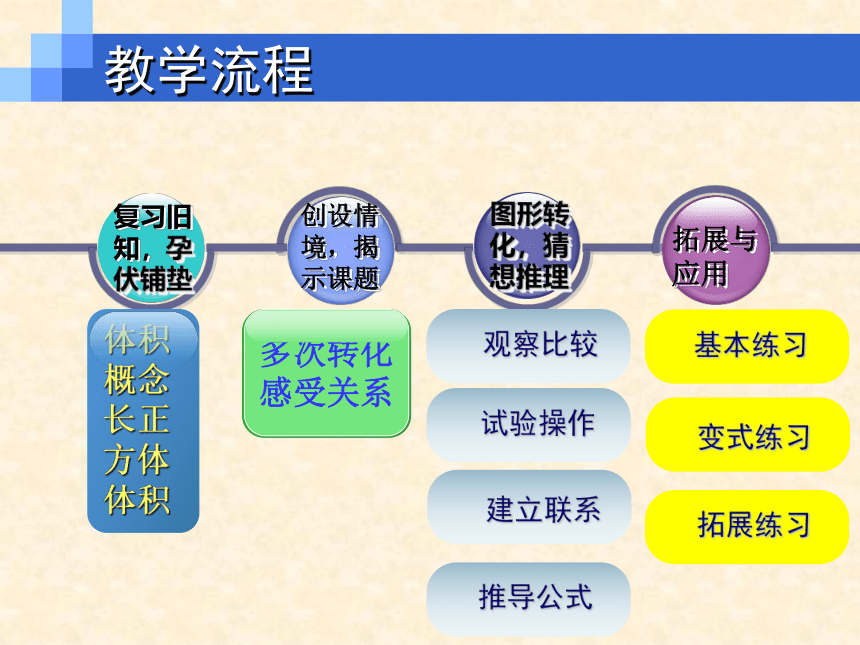
教学流程
复习旧知,孕伏铺垫
创设情境,揭示课题
图形转化,猜想推理
拓展与应用
多次转化
感受关系
体积
概念
长正
方体
体积
试验操作
建立联系
推导公式
基本练习
变式练习
拓展练习
观察比较
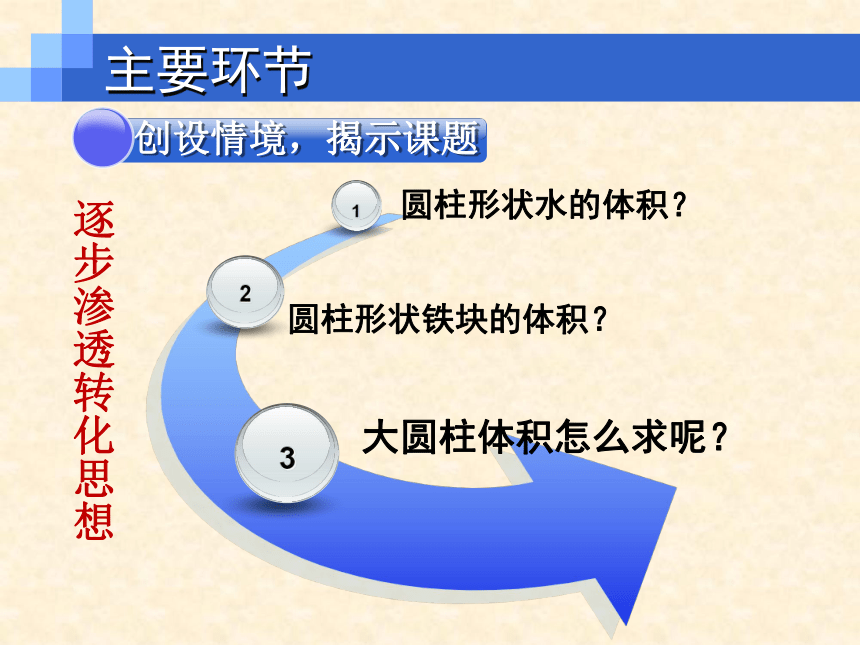
1
圆柱形状水的体积?
2
圆柱形状铁块的体积?
3
大圆柱体积怎么求呢?
主要环节
创设情境,揭示课题
逐步渗透转化思想
学生利用生活经验
,把饮料倒入长、正方体容器求容器的体积,也就是圆柱体饮料的体积,即
将圆柱体积转化成长、正方体体积。
情境1:圆柱体饮料,想知道饮料
罐体积大约是多少?
你有什么办法?
为探索圆柱的体积奠定基础。
情境2:一小块圆柱体铁块的体积
是多少 你有什么办法?
学生观察,借助原有的学习经验得出:圆柱的体积可以借助过去学的不规则物体的体积的排水法可以得到。--调动元认知。
怎样求它们的体积呢
情境3:想知道压路机前轮的体积,
或石柱的体积是多少?
还能用刚才的方法吗?
局限性
探究圆柱体积计算方法
困惑
需求
设计意图:
把握学生已有经验来寻求共鸣。
让学生感受到圆柱体积与长方体体积之间有一定的关系,引导学生思考如何将圆柱体积转化成长方体体积来进行计算-----在潜移默化中渗透“转化”的数学思想和方法。
主要环节
图形转化,猜想推理
1.观察比较,大胆猜想
2.实际操作,验证猜想
3.建立联系,推导公式
问题1:三个几何体有什么联系?
问题2:底面积和高都相等,你想到了什么?为什么?(长方体、正方体的体积相等)
问题3:你还能联想到什么?(圆柱的体积与长方体、正方体的体积可能相等)
1.观察比较、大胆猜想
在等高的情况下,怎样知道体积是否相等?
[设计意图:结合以往学习几何图形的经验,通过等底等高的长、正方体体积关系,引导学生猜想圆柱体积和它们的关系以及体积公式,同时,引导学生将圆柱体积与长、正方体体积联系在一起。为学生下面将圆柱切割、拼补成长方体作铺垫。在无形中提示学生如何“转化”
,确定“转化”方向。]
2.实际操作,验证猜想。
实验验证
引导联想
推导公式
教学中如何突破难点
引导联想
实验验证
推导公式
(1)应把圆柱转化成什么立体图形?
你是怎么想到的
(2)圆柱中的底面是什么形状
圆形使你想到什么?
(3)从圆柱的底面上拨下“一个”圆
形,谁能把这个圆形转化成近
似长方形?
(4)那圆柱呢?你有什么想法吗?(怎样把圆柱转化成长方体 )
问题串:
借助实物模型和多媒体课件演示,让学生直观感受到圆柱体转化为长方体的过程。
引导联想
实验验证
推导公式
问题串(小组):
观察猜想
实验验证
推导公式
我们做了什么?怎么做的?
(2)
在这个过程中,你有什么发现?
(3)
你是怎么发现这些变化的?
(方法的迁移;数学思想的迁移)
(4)
你认为圆柱的体积可以怎样计算?
长方体体积
=
底面积
×
高
圆柱的体积
底面积
高
观察猜想
实验验证
推导公式
=
×
V
=
s
h
强调等价
[设计意图:《标准》明确指出:动手实践、自主探索与合作交流是学生学习数学的重要方式。在圆柱体积的推导过程中,学生在操作中感知,在观察中发现,在比较中得出结论。这样的活动,不仅有助于学生理解所学的知识,而且对于提高自己从事数学活动的能力,对于促进自身的整体发展都有很大的帮助。
同时通过等价的关系,让学生更深刻地了解“转化”思想]
学习效果评价
一根圆柱形木料,横截面积是75平方厘米,长100厘米,它的体积是多少?
底面积
(平方米)
7
7
0.7
高
(米)
3
9
9
体 积
(立方米)
拓展提高
S=πr
C/2
r
h
V
=sh=πr h
V
=sh=c/2×r×h
拓展提高
S侧
2
r
V
=sh=S侧/2×r
=C底×h/2×r
=2πr×h/2×r
=πr h
拓展提高
V
=sh
=r×h×C/2
C/2
r
h
C/2
=S增×C/2
=r×h×2πr/2
=πr h
教学特点
1.注重新知识与旧知识间的联系,多次感悟圆柱与长方体之间的联系。
2.自始至终渗透“转化”思想。
细化转化步骤
方向是
的前提
联想是
的灵魂
等价是
的关键
迁移
联系
推导
--《圆柱的体积》教学设计
背景分析
一
二
三
四
五
我的思考
教学目标
重点难点
教学流程
主要环节
六
说课内容
教学背景分析
课标要求
教材地位
知识内容
经历探究物体大小的过程,掌握转化中的基本关系。
最后一个内容,第一次学习含有曲面的几何体的体积。
理解公式的推导过程,会利用公式计算圆柱的体积。
1
教材的地位和作用
教学背景分析
2
教材分析
复习铺垫
指导转化
寻找关系
归纳公式
圆柱
体积
策略储备
知识储备
教学背景分析
3
学习的基础
什么是圆柱的体积?
怎么计算长方体的体积?
圆能转化成什么图形?
转化的意识
转化的方向
优势:知道圆怎样转化成近似的长方形,
能说出体积概念,
会利用公式求长方体、正方体的体积。
不足:
学生的立体空间观念还不是完全成熟,形体之间的转化还有一定的困难。
教学背景分析
4
学生情况分析
我的思考
学生有必要操作切割好的学具吗?
怎样的设计有利于学生理解?
教学目标
学生理解圆柱体积公式的推导过程,初步掌握圆柱体积的计算公式,并能运用公式正确地计算圆柱的体积。
渗透“转化”的辩证唯物主义思想。
通过观察、迁移、分析自主探究圆柱的体积公式,经历观察—联想—降维的过程,初步体验科学研究的方法。
重点难点
理解圆柱体积公式推导中转化
前后两个立体图形之间的联系。
渗透转化思想、掌握求积公式。
重点
难点
教学流程
复习旧知,孕伏铺垫
创设情境,揭示课题
图形转化,猜想推理
拓展与应用
多次转化
感受关系
体积
概念
长正
方体
体积
试验操作
建立联系
推导公式
基本练习
变式练习
拓展练习
观察比较
1
圆柱形状水的体积?
2
圆柱形状铁块的体积?
3
大圆柱体积怎么求呢?
主要环节
创设情境,揭示课题
逐步渗透转化思想
学生利用生活经验
,把饮料倒入长、正方体容器求容器的体积,也就是圆柱体饮料的体积,即
将圆柱体积转化成长、正方体体积。
情境1:圆柱体饮料,想知道饮料
罐体积大约是多少?
你有什么办法?
为探索圆柱的体积奠定基础。
情境2:一小块圆柱体铁块的体积
是多少 你有什么办法?
学生观察,借助原有的学习经验得出:圆柱的体积可以借助过去学的不规则物体的体积的排水法可以得到。--调动元认知。
怎样求它们的体积呢
情境3:想知道压路机前轮的体积,
或石柱的体积是多少?
还能用刚才的方法吗?
局限性
探究圆柱体积计算方法
困惑
需求
设计意图:
把握学生已有经验来寻求共鸣。
让学生感受到圆柱体积与长方体体积之间有一定的关系,引导学生思考如何将圆柱体积转化成长方体体积来进行计算-----在潜移默化中渗透“转化”的数学思想和方法。
主要环节
图形转化,猜想推理
1.观察比较,大胆猜想
2.实际操作,验证猜想
3.建立联系,推导公式
问题1:三个几何体有什么联系?
问题2:底面积和高都相等,你想到了什么?为什么?(长方体、正方体的体积相等)
问题3:你还能联想到什么?(圆柱的体积与长方体、正方体的体积可能相等)
1.观察比较、大胆猜想
在等高的情况下,怎样知道体积是否相等?
[设计意图:结合以往学习几何图形的经验,通过等底等高的长、正方体体积关系,引导学生猜想圆柱体积和它们的关系以及体积公式,同时,引导学生将圆柱体积与长、正方体体积联系在一起。为学生下面将圆柱切割、拼补成长方体作铺垫。在无形中提示学生如何“转化”
,确定“转化”方向。]
2.实际操作,验证猜想。
实验验证
引导联想
推导公式
教学中如何突破难点
引导联想
实验验证
推导公式
(1)应把圆柱转化成什么立体图形?
你是怎么想到的
(2)圆柱中的底面是什么形状
圆形使你想到什么?
(3)从圆柱的底面上拨下“一个”圆
形,谁能把这个圆形转化成近
似长方形?
(4)那圆柱呢?你有什么想法吗?(怎样把圆柱转化成长方体 )
问题串:
借助实物模型和多媒体课件演示,让学生直观感受到圆柱体转化为长方体的过程。
引导联想
实验验证
推导公式
问题串(小组):
观察猜想
实验验证
推导公式
我们做了什么?怎么做的?
(2)
在这个过程中,你有什么发现?
(3)
你是怎么发现这些变化的?
(方法的迁移;数学思想的迁移)
(4)
你认为圆柱的体积可以怎样计算?
长方体体积
=
底面积
×
高
圆柱的体积
底面积
高
观察猜想
实验验证
推导公式
=
×
V
=
s
h
强调等价
[设计意图:《标准》明确指出:动手实践、自主探索与合作交流是学生学习数学的重要方式。在圆柱体积的推导过程中,学生在操作中感知,在观察中发现,在比较中得出结论。这样的活动,不仅有助于学生理解所学的知识,而且对于提高自己从事数学活动的能力,对于促进自身的整体发展都有很大的帮助。
同时通过等价的关系,让学生更深刻地了解“转化”思想]
学习效果评价
一根圆柱形木料,横截面积是75平方厘米,长100厘米,它的体积是多少?
底面积
(平方米)
7
7
0.7
高
(米)
3
9
9
体 积
(立方米)
拓展提高
S=πr
C/2
r
h
V
=sh=πr h
V
=sh=c/2×r×h
拓展提高
S侧
2
r
V
=sh=S侧/2×r
=C底×h/2×r
=2πr×h/2×r
=πr h
拓展提高
V
=sh
=r×h×C/2
C/2
r
h
C/2
=S增×C/2
=r×h×2πr/2
=πr h
教学特点
1.注重新知识与旧知识间的联系,多次感悟圆柱与长方体之间的联系。
2.自始至终渗透“转化”思想。
细化转化步骤
方向是
的前提
联想是
的灵魂
等价是
的关键
