2020-2021学年黑龙江省哈尔滨市南岗区七年级上学期期末数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市南岗区七年级上学期期末数学试卷(五四学制) (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 673.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 06:23:53 | ||
图片预览



文档简介
2020-2021学年黑龙江省哈尔滨市南岗区七年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列方程中,是一元一次方程的是( )
A.x2﹣4x=3 B.xy﹣3=5 C.3x﹣1= D.x+2y=1
2.如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
3.在平面直角坐标系中,点P(3,4)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
5.下列四个实数中,无理数的是( )
A. B.3.14 C. D.﹣π
6.在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,则点A的坐标为( )
A.(2,0) B.(﹣2,0) C.(0,2) D.(0,﹣2)
7.一个正方体的体积扩大为原来的27倍,则它的棱长变为原来的( )倍.
A.2 B.3 C.4 D.5
8.已知等式ac=bc,则下列等式中不一定成立的是( )
A.ac+1=bc+1 B.ac﹣2=bc﹣2 C.3ac=3bc D.a=b
9.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有x名学生,则依题意所列方程正确的是( )
A.3x﹣20=4x﹣25 B.3x+20=4x+25
C.3x﹣20=4x+25 D.3x+20=4x﹣25
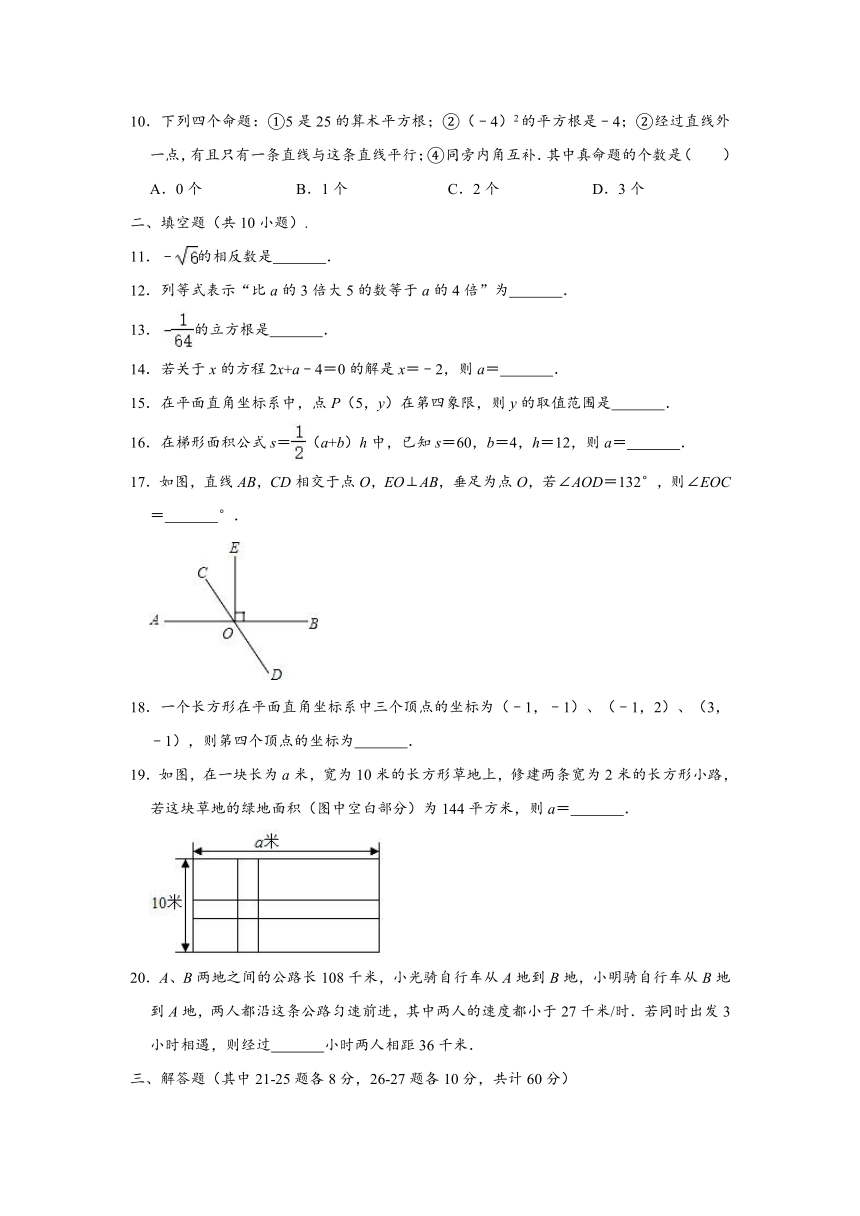
10.下列四个命题:①5是25的算术平方根;②(﹣4)2的平方根是﹣4;②经过直线外一点,有且只有一条直线与这条直线平行;④同旁内角互补.其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
二、填空题(共10小题).
11.﹣的相反数是 .
12.列等式表示“比a的3倍大5的数等于a的4倍”为 .
13.的立方根是 .
14.若关于x的方程2x+a﹣4=0的解是x=﹣2,则a= .
15.在平面直角坐标系中,点P(5,y)在第四象限,则y的取值范围是 .
16.在梯形面积公式s=(a+b)h中,已知s=60,b=4,h=12,则a= .
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
18.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标为 .
19.如图,在一块长为a米,宽为10米的长方形草地上,修建两条宽为2米的长方形小路,若这块草地的绿地面积(图中空白部分)为144平方米,则a= .
20.A、B两地之间的公路长108千米,小光骑自行车从A地到B地,小明骑自行车从B地到A地,两人都沿这条公路匀速前进,其中两人的速度都小于27千米/时.若同时出发3小时相遇,则经过 小时两人相距36千米.
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)计算:
(1);
(2).
22.(8分)解方程:
(1)2x+3x+4x=18;
(2)﹣2=.
23.(8分)如图,AB,CD相交于点E,∠ACE=∠AEC,∠BDE=∠BED,过A作AF⊥BD,垂足为F.求证:AC⊥AF.
证明:∵∠ACE=∠AEC,∠BDE=∠BED.
又∠AEC=∠BED,( )
∴∠ACE=∠BDE.
∴AC∥DB.( )
∴∠CAF=∠AFD.( )
∵AF⊥DB,
∴∠AFD=90°.( )
∴∠CAF=90°.
∴AC⊥AF.
24.(8分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
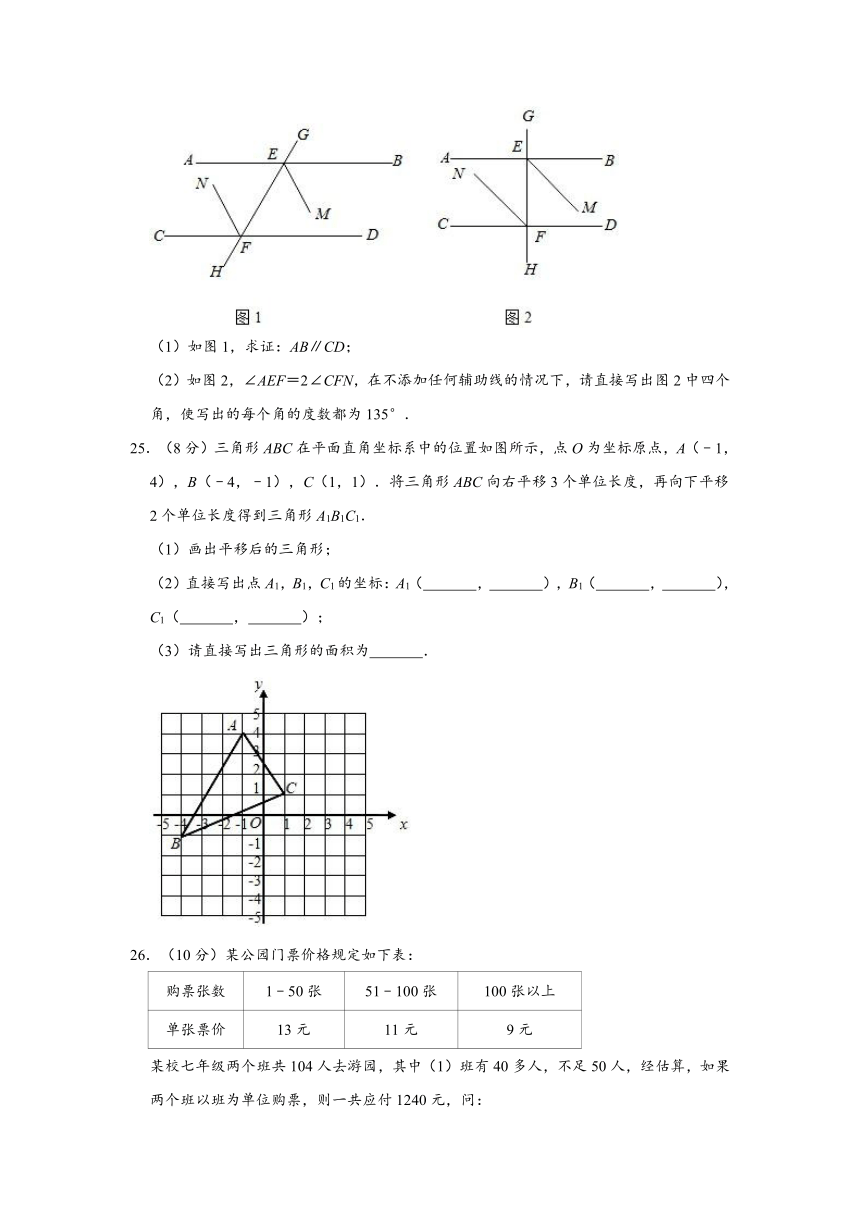
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
25.(8分)三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(﹣1,4),B(﹣4,﹣1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1.
(1)画出平移后的三角形;
(2)直接写出点A1,B1,C1的坐标:A1( , ),B1( , ),C1( , );
(3)请直接写出三角形的面积为 .
26.(10分)某公园门票价格规定如下表:
购票张数 1﹣50张 51﹣100张 100张以上
单张票价 13元 11元 9元
某校七年级两个班共104人去游园,其中(1)班有40多人,不足50人,经估算,如果两个班以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
27.(10分)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
参考答案
一、选择题(共10小题).
1.下列方程中,是一元一次方程的是( )
A.x2﹣4x=3 B.xy﹣3=5 C.3x﹣1= D.x+2y=1
解:A、是一元二次方程,不是一元一次方程,故本选项不符合题意;
B、是二元二次方程,不是一元一次方程,故本选项不符合题意;
C、是一元一次方程,故本选项符合题意;
D、是二元一次方程,不是一元一次方程,故本选项不符合题意;
故选:C.
2.如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
解:在同一平面内,与已知直线垂直的直线有无数条,
所以作已知直线m的垂线,可作无数条.
故选:D.
3.在平面直角坐标系中,点P(3,4)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵3>0,4>0,
∴点P(3,4)位于第一象限.
故选:A.
4.在下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
解:A、∠1与∠2不是对顶角;
B、∠1与∠2是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2不是对顶角;
故选:B.
5.下列四个实数中,无理数的是( )
A. B.3.14 C. D.﹣π
【解答】解;A、=4,不是无理数,错误;
B、3.14不是无理数,错误;
C、不是无理数,错误;
D、﹣π是无理数,正确;
故选:D.
6.在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,则点A的坐标为( )
A.(2,0) B.(﹣2,0) C.(0,2) D.(0,﹣2)
解:∵在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,
∴A点的坐标是(0,2),
故选:C.
7.一个正方体的体积扩大为原来的27倍,则它的棱长变为原来的( )倍.
A.2 B.3 C.4 D.5
解:一个正方体的体积扩大为原来的27倍,它的棱长变为原来的倍,即3倍.
故选:B.
8.已知等式ac=bc,则下列等式中不一定成立的是( )
A.ac+1=bc+1 B.ac﹣2=bc﹣2 C.3ac=3bc D.a=b
解:A、ac=bc两边都加1,原变形正确,故此选项不符合题意;
B、ac=bc两边都减去2,原变形正确,故此选项不符合题意;
C、ac=bc两边都乘以3,原变形正确,故此选项不符合题意;
D、ac=bc两边都除以c,条件是c≠0,原变形不一定成立,故此选项符合题意;
故选:D.
9.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有x名学生,则依题意所列方程正确的是( )
A.3x﹣20=4x﹣25 B.3x+20=4x+25
C.3x﹣20=4x+25 D.3x+20=4x﹣25
解:设这个班有学生x人,
由题意得,3x+20=4x﹣25.
故选:D.
10.下列四个命题:①5是25的算术平方根;②(﹣4)2的平方根是﹣4;②经过直线外一点,有且只有一条直线与这条直线平行;④同旁内角互补.其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
解:①5是25的算术平方根,本小题说法是真命题;
②∵(﹣4)2的平方根是±4,
∴本小题说法是假命题;
②经过直线外一点,有且只有一条直线与这条直线平行,本小题说法是真命题;
④∵两直线平行,同旁内角互补,
∴本小题说法是假命题;
故选:C.
二、填空题(共10小题).
11.﹣的相反数是 .
解:﹣的相反数是:.
故答案为:.
12.列等式表示“比a的3倍大5的数等于a的4倍”为 3a+5=4a .
解:由题意,得
3a+5=4a,
故答案为:3a+5=4a.
13.的立方根是 .
解:∵=,
∴的立方根是,
故答案为:.
14.若关于x的方程2x+a﹣4=0的解是x=﹣2,则a= 8 .
解:把x=﹣2代入方程2x+a﹣4=0,得2×(﹣2)+a﹣4=0,解得a=8,
故答案为:8.
15.在平面直角坐标系中,点P(5,y)在第四象限,则y的取值范围是 y<0 .
解:∵点P(5,y)在第四象限,
∴y<0.
故答案为y<0.
16.在梯形面积公式s=(a+b)h中,已知s=60,b=4,h=12,则a= 6 .
解:把s=60,b=4,h=12代入公式s=h(a+b)得:60=×12×(a+4),
解得:a=6,
故答案为:6
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= 42 °.
解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,
故答案为:42.
18.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标为 (3,2) .
解:过(﹣1,2)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,2),即为第四个顶点坐标.故答案为(3,2).
19.如图,在一块长为a米,宽为10米的长方形草地上,修建两条宽为2米的长方形小路,若这块草地的绿地面积(图中空白部分)为144平方米,则a= 20 .
解:除小路外的部分可合成长(a﹣2)米,宽(10﹣2)米的长方形,
依题意得:(a﹣2)(10﹣2)=144,
解得:a=20.
故答案为:20.
20.A、B两地之间的公路长108千米,小光骑自行车从A地到B地,小明骑自行车从B地到A地,两人都沿这条公路匀速前进,其中两人的速度都小于27千米/时.若同时出发3小时相遇,则经过 2或4 小时两人相距36千米.
解:设经过x小时两人相距36千米,
当两人没有相遇前,,
解得:x=2,
当两人相遇后,,
解得x=4,
综上所述:经过2或4小时两人相距36千米,
故答案为:2或4.
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)计算:
(1);
(2).
解:(1)
=
=.
(2)
=0.2﹣2﹣0.25
=﹣2.05.
22.(8分)解方程:
(1)2x+3x+4x=18;
(2)﹣2=.
解:(1)合并得:9x=18,
解得:x=2;
(2)去分母得:2(x+1)﹣8=x,
去括号得:2x+2﹣8=x,
移项得:2x﹣x=﹣2+8,
解得:x=6.
23.(8分)如图,AB,CD相交于点E,∠ACE=∠AEC,∠BDE=∠BED,过A作AF⊥BD,垂足为F.求证:AC⊥AF.
证明:∵∠ACE=∠AEC,∠BDE=∠BED.
又∠AEC=∠BED,( 对顶角相等 )
∴∠ACE=∠BDE.
∴AC∥DB.( 内错角相等,两直线平行 )
∴∠CAF=∠AFD.( 两直线平行,内错角相等 )
∵AF⊥DB,
∴∠AFD=90°.( 垂直定义 )
∴∠CAF=90°.
∴AC⊥AF.
【解答】证明:∵∠ACE=∠AEC,∠BDE=∠BED.
又∠AEC=∠BED,(对顶角相等)
∴∠ACE=∠BDE.
∴AC∥DB.(内错角相等,两直线平行)
∴∠CAF=∠AFD.(两直线平行,内错角相等)
∵AF⊥DB,
∴∠AFD=90°.(垂直定义)
∴∠CAF=90°.
∴AC⊥AF.
故答案为:对顶角相等;内错角相等,两直线平行;两直线平行,内错角相等;垂直定义.
24.(8分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
【解答】(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
25.(8分)三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(﹣1,4),B(﹣4,﹣1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1.
(1)画出平移后的三角形;
(2)直接写出点A1,B1,C1的坐标:A1( 2 , 2 ),B1( ﹣1 , ﹣3 ),C1( 4 , ﹣1 );
(3)请直接写出三角形的面积为 .
解:(1)如图所示,
△A1B1C1即为所求.
(2)A1(2,2),B1(﹣1,﹣3),C1(4,﹣1),
(3)△ABC的面积==,
故答案为:(2)2;2;﹣1;﹣3;4;﹣1;(3).
26.(10分)某公园门票价格规定如下表:
购票张数 1﹣50张 51﹣100张 100张以上
单张票价 13元 11元 9元
某校七年级两个班共104人去游园,其中(1)班有40多人,不足50人,经估算,如果两个班以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
解:(1)设(1)班有x个学生,则(2)班有(104﹣x)个学生,
根据题意得:13x+11(104﹣x)=1240,
解得:x=48,
∴104﹣x=56.
答:七年级(1)班有48个学生,七年级(2)班有56个学生.
(2)1240﹣9×104=304(元).
答:如果两班联合起来,作为一个团体购票,可省304元钱.
(3)51×11=561(元),48×13=624(元),
∴561<624,
∴如果七年级(1)班单独组织去游园,购买51张门票最省钱.
27.(10分)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
【解答】(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
一、选择题(共10小题).
1.下列方程中,是一元一次方程的是( )
A.x2﹣4x=3 B.xy﹣3=5 C.3x﹣1= D.x+2y=1
2.如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
3.在平面直角坐标系中,点P(3,4)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
5.下列四个实数中,无理数的是( )
A. B.3.14 C. D.﹣π
6.在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,则点A的坐标为( )
A.(2,0) B.(﹣2,0) C.(0,2) D.(0,﹣2)
7.一个正方体的体积扩大为原来的27倍,则它的棱长变为原来的( )倍.
A.2 B.3 C.4 D.5
8.已知等式ac=bc,则下列等式中不一定成立的是( )
A.ac+1=bc+1 B.ac﹣2=bc﹣2 C.3ac=3bc D.a=b
9.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有x名学生,则依题意所列方程正确的是( )
A.3x﹣20=4x﹣25 B.3x+20=4x+25
C.3x﹣20=4x+25 D.3x+20=4x﹣25
10.下列四个命题:①5是25的算术平方根;②(﹣4)2的平方根是﹣4;②经过直线外一点,有且只有一条直线与这条直线平行;④同旁内角互补.其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
二、填空题(共10小题).
11.﹣的相反数是 .
12.列等式表示“比a的3倍大5的数等于a的4倍”为 .
13.的立方根是 .
14.若关于x的方程2x+a﹣4=0的解是x=﹣2,则a= .
15.在平面直角坐标系中,点P(5,y)在第四象限,则y的取值范围是 .
16.在梯形面积公式s=(a+b)h中,已知s=60,b=4,h=12,则a= .
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
18.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标为 .
19.如图,在一块长为a米,宽为10米的长方形草地上,修建两条宽为2米的长方形小路,若这块草地的绿地面积(图中空白部分)为144平方米,则a= .
20.A、B两地之间的公路长108千米,小光骑自行车从A地到B地,小明骑自行车从B地到A地,两人都沿这条公路匀速前进,其中两人的速度都小于27千米/时.若同时出发3小时相遇,则经过 小时两人相距36千米.
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)计算:
(1);
(2).
22.(8分)解方程:
(1)2x+3x+4x=18;
(2)﹣2=.
23.(8分)如图,AB,CD相交于点E,∠ACE=∠AEC,∠BDE=∠BED,过A作AF⊥BD,垂足为F.求证:AC⊥AF.
证明:∵∠ACE=∠AEC,∠BDE=∠BED.
又∠AEC=∠BED,( )
∴∠ACE=∠BDE.
∴AC∥DB.( )
∴∠CAF=∠AFD.( )
∵AF⊥DB,
∴∠AFD=90°.( )
∴∠CAF=90°.
∴AC⊥AF.
24.(8分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
25.(8分)三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(﹣1,4),B(﹣4,﹣1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1.
(1)画出平移后的三角形;
(2)直接写出点A1,B1,C1的坐标:A1( , ),B1( , ),C1( , );
(3)请直接写出三角形的面积为 .
26.(10分)某公园门票价格规定如下表:
购票张数 1﹣50张 51﹣100张 100张以上
单张票价 13元 11元 9元
某校七年级两个班共104人去游园,其中(1)班有40多人,不足50人,经估算,如果两个班以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
27.(10分)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
参考答案
一、选择题(共10小题).
1.下列方程中,是一元一次方程的是( )
A.x2﹣4x=3 B.xy﹣3=5 C.3x﹣1= D.x+2y=1
解:A、是一元二次方程,不是一元一次方程,故本选项不符合题意;
B、是二元二次方程,不是一元一次方程,故本选项不符合题意;
C、是一元一次方程,故本选项符合题意;
D、是二元一次方程,不是一元一次方程,故本选项不符合题意;
故选:C.
2.如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
解:在同一平面内,与已知直线垂直的直线有无数条,
所以作已知直线m的垂线,可作无数条.
故选:D.
3.在平面直角坐标系中,点P(3,4)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵3>0,4>0,
∴点P(3,4)位于第一象限.
故选:A.
4.在下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
解:A、∠1与∠2不是对顶角;
B、∠1与∠2是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2不是对顶角;
故选:B.
5.下列四个实数中,无理数的是( )
A. B.3.14 C. D.﹣π
【解答】解;A、=4,不是无理数,错误;
B、3.14不是无理数,错误;
C、不是无理数,错误;
D、﹣π是无理数,正确;
故选:D.
6.在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,则点A的坐标为( )
A.(2,0) B.(﹣2,0) C.(0,2) D.(0,﹣2)
解:∵在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,
∴A点的坐标是(0,2),
故选:C.
7.一个正方体的体积扩大为原来的27倍,则它的棱长变为原来的( )倍.
A.2 B.3 C.4 D.5
解:一个正方体的体积扩大为原来的27倍,它的棱长变为原来的倍,即3倍.
故选:B.
8.已知等式ac=bc,则下列等式中不一定成立的是( )
A.ac+1=bc+1 B.ac﹣2=bc﹣2 C.3ac=3bc D.a=b
解:A、ac=bc两边都加1,原变形正确,故此选项不符合题意;
B、ac=bc两边都减去2,原变形正确,故此选项不符合题意;
C、ac=bc两边都乘以3,原变形正确,故此选项不符合题意;
D、ac=bc两边都除以c,条件是c≠0,原变形不一定成立,故此选项符合题意;
故选:D.
9.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有x名学生,则依题意所列方程正确的是( )
A.3x﹣20=4x﹣25 B.3x+20=4x+25
C.3x﹣20=4x+25 D.3x+20=4x﹣25
解:设这个班有学生x人,
由题意得,3x+20=4x﹣25.
故选:D.
10.下列四个命题:①5是25的算术平方根;②(﹣4)2的平方根是﹣4;②经过直线外一点,有且只有一条直线与这条直线平行;④同旁内角互补.其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
解:①5是25的算术平方根,本小题说法是真命题;
②∵(﹣4)2的平方根是±4,
∴本小题说法是假命题;
②经过直线外一点,有且只有一条直线与这条直线平行,本小题说法是真命题;
④∵两直线平行,同旁内角互补,
∴本小题说法是假命题;
故选:C.
二、填空题(共10小题).
11.﹣的相反数是 .
解:﹣的相反数是:.
故答案为:.
12.列等式表示“比a的3倍大5的数等于a的4倍”为 3a+5=4a .
解:由题意,得
3a+5=4a,
故答案为:3a+5=4a.
13.的立方根是 .
解:∵=,
∴的立方根是,
故答案为:.
14.若关于x的方程2x+a﹣4=0的解是x=﹣2,则a= 8 .
解:把x=﹣2代入方程2x+a﹣4=0,得2×(﹣2)+a﹣4=0,解得a=8,
故答案为:8.
15.在平面直角坐标系中,点P(5,y)在第四象限,则y的取值范围是 y<0 .
解:∵点P(5,y)在第四象限,
∴y<0.
故答案为y<0.
16.在梯形面积公式s=(a+b)h中,已知s=60,b=4,h=12,则a= 6 .
解:把s=60,b=4,h=12代入公式s=h(a+b)得:60=×12×(a+4),
解得:a=6,
故答案为:6
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= 42 °.
解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,
故答案为:42.
18.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标为 (3,2) .
解:过(﹣1,2)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,2),即为第四个顶点坐标.故答案为(3,2).
19.如图,在一块长为a米,宽为10米的长方形草地上,修建两条宽为2米的长方形小路,若这块草地的绿地面积(图中空白部分)为144平方米,则a= 20 .
解:除小路外的部分可合成长(a﹣2)米,宽(10﹣2)米的长方形,
依题意得:(a﹣2)(10﹣2)=144,
解得:a=20.
故答案为:20.
20.A、B两地之间的公路长108千米,小光骑自行车从A地到B地,小明骑自行车从B地到A地,两人都沿这条公路匀速前进,其中两人的速度都小于27千米/时.若同时出发3小时相遇,则经过 2或4 小时两人相距36千米.
解:设经过x小时两人相距36千米,
当两人没有相遇前,,
解得:x=2,
当两人相遇后,,
解得x=4,
综上所述:经过2或4小时两人相距36千米,
故答案为:2或4.
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)计算:
(1);
(2).
解:(1)
=
=.
(2)
=0.2﹣2﹣0.25
=﹣2.05.
22.(8分)解方程:
(1)2x+3x+4x=18;
(2)﹣2=.
解:(1)合并得:9x=18,
解得:x=2;
(2)去分母得:2(x+1)﹣8=x,
去括号得:2x+2﹣8=x,
移项得:2x﹣x=﹣2+8,
解得:x=6.
23.(8分)如图,AB,CD相交于点E,∠ACE=∠AEC,∠BDE=∠BED,过A作AF⊥BD,垂足为F.求证:AC⊥AF.
证明:∵∠ACE=∠AEC,∠BDE=∠BED.
又∠AEC=∠BED,( 对顶角相等 )
∴∠ACE=∠BDE.
∴AC∥DB.( 内错角相等,两直线平行 )
∴∠CAF=∠AFD.( 两直线平行,内错角相等 )
∵AF⊥DB,
∴∠AFD=90°.( 垂直定义 )
∴∠CAF=90°.
∴AC⊥AF.
【解答】证明:∵∠ACE=∠AEC,∠BDE=∠BED.
又∠AEC=∠BED,(对顶角相等)
∴∠ACE=∠BDE.
∴AC∥DB.(内错角相等,两直线平行)
∴∠CAF=∠AFD.(两直线平行,内错角相等)
∵AF⊥DB,
∴∠AFD=90°.(垂直定义)
∴∠CAF=90°.
∴AC⊥AF.
故答案为:对顶角相等;内错角相等,两直线平行;两直线平行,内错角相等;垂直定义.
24.(8分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
【解答】(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
25.(8分)三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(﹣1,4),B(﹣4,﹣1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1.
(1)画出平移后的三角形;
(2)直接写出点A1,B1,C1的坐标:A1( 2 , 2 ),B1( ﹣1 , ﹣3 ),C1( 4 , ﹣1 );
(3)请直接写出三角形的面积为 .
解:(1)如图所示,
△A1B1C1即为所求.
(2)A1(2,2),B1(﹣1,﹣3),C1(4,﹣1),
(3)△ABC的面积==,
故答案为:(2)2;2;﹣1;﹣3;4;﹣1;(3).
26.(10分)某公园门票价格规定如下表:
购票张数 1﹣50张 51﹣100张 100张以上
单张票价 13元 11元 9元
某校七年级两个班共104人去游园,其中(1)班有40多人,不足50人,经估算,如果两个班以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
解:(1)设(1)班有x个学生,则(2)班有(104﹣x)个学生,
根据题意得:13x+11(104﹣x)=1240,
解得:x=48,
∴104﹣x=56.
答:七年级(1)班有48个学生,七年级(2)班有56个学生.
(2)1240﹣9×104=304(元).
答:如果两班联合起来,作为一个团体购票,可省304元钱.
(3)51×11=561(元),48×13=624(元),
∴561<624,
∴如果七年级(1)班单独组织去游园,购买51张门票最省钱.
27.(10分)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
【解答】(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
同课章节目录
