27.2.1第3课时 相似三角形的判定定理3-2021春人教版九年级数学下册习题课件(19张)
文档属性
| 名称 | 27.2.1第3课时 相似三角形的判定定理3-2021春人教版九年级数学下册习题课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览






文档简介
第二十七章 相 似
九年级数学下册人教版
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 相似三角形的判定定理3
知识点一 两角分别相等的两个三角形相似
1.有一个角为30°的两个直角三角形一定( )
A.全等 B.相似
C.既全等又相似 D.无法确定
B
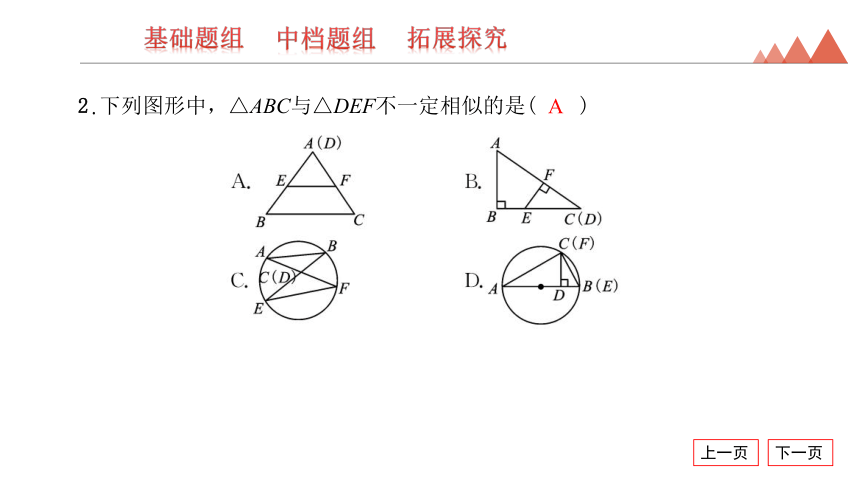
2.下列图形中,△ABC与△DEF不一定相似的是( )
A
3.如图,在△ABC中,∠AED=∠B,则下列等式成立的是( )
A. = B. =
C. = D. =
C
4.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2 ,AB=3,则BD=________.
5.如图,AB∥DE,AC∥DF,点B,E,C,F在一条直线上,求证:△ABC∽△DEF.
证明:∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F,∴△ABC∽△DEF.
知识点二 斜边和一条直角边成比例的两个直角三角形相似
6.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是( )
A.∠B=∠B1 B. =
C. = D. =
D
7.已知Rt△ABC中,∠C=90°,AB=15 cm,BC=8 cm,另一个Rt△DEF中,∠D=90°,EF= cm,DE=6 cm,则△ABC与△DEF________
(填“是”或“不是”)相似的两个三角形.
是
8.如图,已知∠ACB=∠ADC=90°,AD=2,CD=2,当AB的长为________时,△ACB与△ADC相似.
4
9.已知AB是半圆的直径,AC,BC分别与半圆相交于点E,D,BE与AD相交于点F,求证:EF·BF=AF·DF.
证明:由题意,得∠AEF=∠BDF.又∵∠AFE=∠BFD,∴△AEF∽△BDF,∴ ,即EF·BF=AF·DF.
10.如图,点P在△ABC的边AC上,如果添加一个条件后可以得到△ABP∽△ACB,那么以下添加的条件中,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.AB2=AP·AC
D. =
D
11.如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN=________.
4
12.如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则点C的坐标是________.
【思路提示】在光的反射中,反射角等于入射角.
(2,0)
13.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,求AE的长.
解:∵△ABC是边长为9的等边三角形,∴∠B=∠C=60°,AB=BC=AC=9,∴∠BAD+∠ADB=120°.∵∠ADE=60°,∴∠CDE+∠ADB=120°,∴∠BAD=∠CDE.又∵∠B=∠C,∴△ABD∽△DCE,∴ ,即
= ,∴CE=2.∴AE=AC-CE=9-2=7.
14.(2018·抚顺)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,E为BC上一点,连接AE,作EF⊥AE交AB于点F.
(1)求证:△AGC∽△EFB;
证明:∵CD⊥AB,EF⊥AE,∴∠FDG=∠FEG=90°,∴∠DGE+∠DFE=360°-90°-90°=180°.∵∠BFE+∠DFE=180°,∴∠BFE=∠DGE.∵∠DGE=∠AGC,∴∠AGC=∠BFE.∵∠ACB=∠FEG=90°,∴∠AEC+∠EAC=90°,∠AEC+∠BEF=180°-90°=90°,∴∠EAC=∠BEF,∴△AGC∽△EFB.
(2)除(1)中相似三角形,图中还有其他相似三角形吗?如果有,请把它们都写出来.
解:有.△AGD∽△AFE,△ACD∽△ABC∽△CBD.
15.如图,在矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
证明:∵四边形ABCD是矩形,∴AB∥CD,∴△APQ∽△CDQ.
(2)点P从点A出发沿AB边以每秒1个单位长度的速度向点B移动,移动时间为t秒,当t为何值时,DP⊥AC?
解:∵DP⊥AC,∴∠DQA=90°,∴∠ADQ+∠DAQ=90°.∵四边形ABCD为矩形,∴AD=BC=10,∠DAP=∠B=90°,∴∠DAQ+∠PAQ=90°,∴∠ADQ=∠PAQ,∴△DAP∽△ABC,∴
,即 ,∴AP=5,∴t=5.即当t=5时,DP⊥AC.
1.充分利用图中的隐含条件,一般地,图中的公共角、对顶角是寻求两角相等的条件.
2.证明等积式ad=bc,一般利用相似三角形来证明,关键是将等积式ad=bc转化成比例式 = ,然后寻找分别以a,c和b,d为对应边的三角形(或分别以a,b和c,d为对应边的三角形),再证明这两个三角形相似.)
九年级数学下册人教版
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 相似三角形的判定定理3
知识点一 两角分别相等的两个三角形相似
1.有一个角为30°的两个直角三角形一定( )
A.全等 B.相似
C.既全等又相似 D.无法确定
B
2.下列图形中,△ABC与△DEF不一定相似的是( )
A
3.如图,在△ABC中,∠AED=∠B,则下列等式成立的是( )
A. = B. =
C. = D. =
C
4.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2 ,AB=3,则BD=________.
5.如图,AB∥DE,AC∥DF,点B,E,C,F在一条直线上,求证:△ABC∽△DEF.
证明:∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F,∴△ABC∽△DEF.
知识点二 斜边和一条直角边成比例的两个直角三角形相似
6.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是( )
A.∠B=∠B1 B. =
C. = D. =
D
7.已知Rt△ABC中,∠C=90°,AB=15 cm,BC=8 cm,另一个Rt△DEF中,∠D=90°,EF= cm,DE=6 cm,则△ABC与△DEF________
(填“是”或“不是”)相似的两个三角形.
是
8.如图,已知∠ACB=∠ADC=90°,AD=2,CD=2,当AB的长为________时,△ACB与△ADC相似.
4
9.已知AB是半圆的直径,AC,BC分别与半圆相交于点E,D,BE与AD相交于点F,求证:EF·BF=AF·DF.
证明:由题意,得∠AEF=∠BDF.又∵∠AFE=∠BFD,∴△AEF∽△BDF,∴ ,即EF·BF=AF·DF.
10.如图,点P在△ABC的边AC上,如果添加一个条件后可以得到△ABP∽△ACB,那么以下添加的条件中,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.AB2=AP·AC
D. =
D
11.如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN=________.
4
12.如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则点C的坐标是________.
【思路提示】在光的反射中,反射角等于入射角.
(2,0)
13.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,求AE的长.
解:∵△ABC是边长为9的等边三角形,∴∠B=∠C=60°,AB=BC=AC=9,∴∠BAD+∠ADB=120°.∵∠ADE=60°,∴∠CDE+∠ADB=120°,∴∠BAD=∠CDE.又∵∠B=∠C,∴△ABD∽△DCE,∴ ,即
= ,∴CE=2.∴AE=AC-CE=9-2=7.
14.(2018·抚顺)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,E为BC上一点,连接AE,作EF⊥AE交AB于点F.
(1)求证:△AGC∽△EFB;
证明:∵CD⊥AB,EF⊥AE,∴∠FDG=∠FEG=90°,∴∠DGE+∠DFE=360°-90°-90°=180°.∵∠BFE+∠DFE=180°,∴∠BFE=∠DGE.∵∠DGE=∠AGC,∴∠AGC=∠BFE.∵∠ACB=∠FEG=90°,∴∠AEC+∠EAC=90°,∠AEC+∠BEF=180°-90°=90°,∴∠EAC=∠BEF,∴△AGC∽△EFB.
(2)除(1)中相似三角形,图中还有其他相似三角形吗?如果有,请把它们都写出来.
解:有.△AGD∽△AFE,△ACD∽△ABC∽△CBD.
15.如图,在矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
证明:∵四边形ABCD是矩形,∴AB∥CD,∴△APQ∽△CDQ.
(2)点P从点A出发沿AB边以每秒1个单位长度的速度向点B移动,移动时间为t秒,当t为何值时,DP⊥AC?
解:∵DP⊥AC,∴∠DQA=90°,∴∠ADQ+∠DAQ=90°.∵四边形ABCD为矩形,∴AD=BC=10,∠DAP=∠B=90°,∴∠DAQ+∠PAQ=90°,∴∠ADQ=∠PAQ,∴△DAP∽△ABC,∴
,即 ,∴AP=5,∴t=5.即当t=5时,DP⊥AC.
1.充分利用图中的隐含条件,一般地,图中的公共角、对顶角是寻求两角相等的条件.
2.证明等积式ad=bc,一般利用相似三角形来证明,关键是将等积式ad=bc转化成比例式 = ,然后寻找分别以a,c和b,d为对应边的三角形(或分别以a,b和c,d为对应边的三角形),再证明这两个三角形相似.)
