29.2 直线与圆的位置关系-2021春冀教版九年级数学下册课件(25张)
文档属性
| 名称 | 29.2 直线与圆的位置关系-2021春冀教版九年级数学下册课件(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 390.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览






文档简介
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
1
1.直线与圆的位置关系
2
2.直线与圆的位置关系的数量表示
CONTENTS
1
新知导入
想一想:
(地平线)
你发现这个自然现象反映出直线和圆的公共点个数有 种情况
三
CONTENTS
2
课程讲授
直线与圆的位置关系
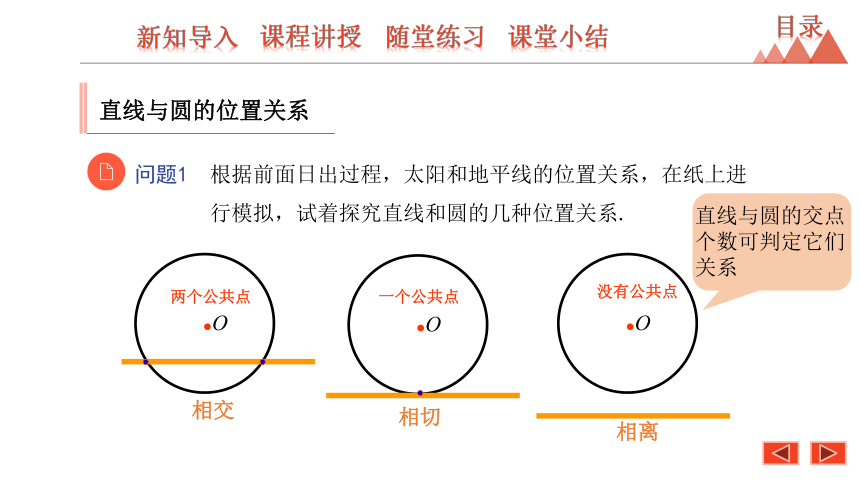
问题1 根据前面日出过程,太阳和地平线的位置关系,在纸上进
行模拟,试着探究直线和圆的几种位置关系.
●O
●O
相交
●O
相切
相离
直线与圆的交点个数可判定它们关系
两个公共点
没有公共点
一个公共点
直线与圆的位置关系
O
l
P
Q
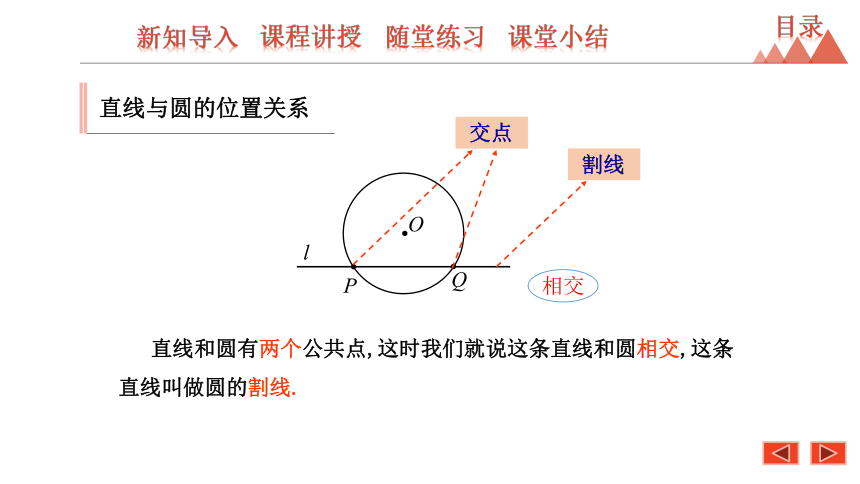
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
相交
交点
割线
直线与圆的位置关系
O
l
P
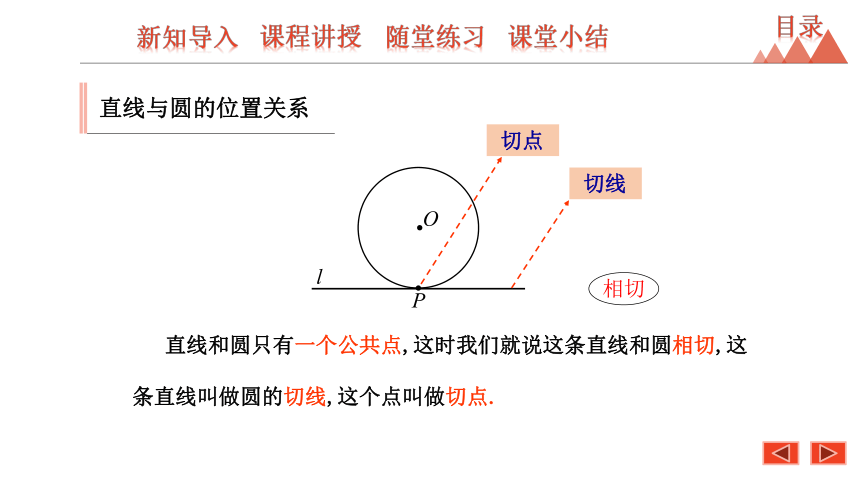
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
相切
切点
切线
直线与圆的位置关系
O
l
直线和圆没有公共点,这时我们就说这条直线和圆相离.
相离
直线与圆的位置关系
归纳:直线与圆无公共点 直线与圆相离;
直线与圆有唯一一个公共点 直线与圆相切;
直线与圆有两个公共点 直线与圆相交.
d r;
(1)直线和圆相交
直线与圆的位置关系的数量表示
问题1.1 如图,设⊙O的半径为r,圆心O到直线l的距离为d,当l与
⊙O相交、相切或相离时,r与d分别具有怎样的数量关系?
r
r
r
d
┐
d
┐
┐
d
O
l
P
Q
O
l
P
O
l
<
d r;
(2)直线和圆相切
=
d r;
(3)直线和圆相离
>
直线与圆的位置关系的数量表示
问题1.2 当d<r,d=r或d>r时,l与⊙O分别具有怎样的位置关系?
r
r
r
d
┐
d
┐
┐
d
O
l
P
Q
O
l
P
O
l
(1)d<r
直线和圆______
(2)d=r
直线和圆______
(3)d>r
直线和圆______
相交
相切
相离
直线与圆的位置关系的数量表示
归纳:直线l和⊙O相交 ___________
直线l和⊙O相切 ___________
直线l和⊙O相离 ___________
d>r
d=r
d直线与圆的位置关系的数量表示
例 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,2cm,
2.4cm,3cm为半径画⊙C,斜边AB分别与⊙C有怎样的位置关系?
为什么?
A
B
C
提示:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
直线与圆的位置关系的数量表示
解:过C作CD⊥AB,垂足为D.
在Rt△ABC中,
AB=
5.
由三角形的面积公式,并整理,得
∴
即圆心C到AB的距离d=2.4cm.
当r=2cm时,
d >r,
斜边AB⊙C和相离.
D
当r=2.4cm时,
d =r,
斜边AB⊙C和相切.
当r=3cm时,
d <r,
斜边AB⊙C和相交.
A
B
C
直线与圆的位置关系的数量表示
归纳:一判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 的个数来判断;
(2)由 的大小关系来判断;
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
直线与圆的位置关系的数量表示
练一练:已知⊙O的面积为9π cm2,若点O到直线l的距离为π cm,
则直线l与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
C
CONTENTS
3
随堂练习
1.直线l与半径为r的⊙O相交,且圆心O到直线l的距离为5,则半径r的取值范围是( )
A.r>5
B.r=5
C.0<r<5
D.0<r≤5
A
2.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情况均有可能
C
3.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
C
4.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
B
5.如图,已知∠AOB=30°,M为OA边上一点,以点M为圆心,2 cm为半径作⊙M.若点M在OA边上运动,则OM=_______cm时,⊙M与OB相切.
6.在直角坐标系中,⊙M的圆心坐标是(m,0),半径是2,如果⊙M与y轴所在的直线相切,那么m=_____;如果⊙M与y轴所在的直线相交,那么m的取值范围是____________.
4
±2
-2<m<2
CONTENTS
4
课堂小结
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;
1个:相切;
2个:相交
d>r:相离
d=r:相切
d
29.2 直线与圆的位置关系
1
1.直线与圆的位置关系
2
2.直线与圆的位置关系的数量表示
CONTENTS
1
新知导入
想一想:
(地平线)
你发现这个自然现象反映出直线和圆的公共点个数有 种情况
三
CONTENTS
2
课程讲授
直线与圆的位置关系
问题1 根据前面日出过程,太阳和地平线的位置关系,在纸上进
行模拟,试着探究直线和圆的几种位置关系.
●O
●O
相交
●O
相切
相离
直线与圆的交点个数可判定它们关系
两个公共点
没有公共点
一个公共点
直线与圆的位置关系
O
l
P
Q
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
相交
交点
割线
直线与圆的位置关系
O
l
P
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
相切
切点
切线
直线与圆的位置关系
O
l
直线和圆没有公共点,这时我们就说这条直线和圆相离.
相离
直线与圆的位置关系
归纳:直线与圆无公共点 直线与圆相离;
直线与圆有唯一一个公共点 直线与圆相切;
直线与圆有两个公共点 直线与圆相交.
d r;
(1)直线和圆相交
直线与圆的位置关系的数量表示
问题1.1 如图,设⊙O的半径为r,圆心O到直线l的距离为d,当l与
⊙O相交、相切或相离时,r与d分别具有怎样的数量关系?
r
r
r
d
┐
d
┐
┐
d
O
l
P
Q
O
l
P
O
l
<
d r;
(2)直线和圆相切
=
d r;
(3)直线和圆相离
>
直线与圆的位置关系的数量表示
问题1.2 当d<r,d=r或d>r时,l与⊙O分别具有怎样的位置关系?
r
r
r
d
┐
d
┐
┐
d
O
l
P
Q
O
l
P
O
l
(1)d<r
直线和圆______
(2)d=r
直线和圆______
(3)d>r
直线和圆______
相交
相切
相离
直线与圆的位置关系的数量表示
归纳:直线l和⊙O相交 ___________
直线l和⊙O相切 ___________
直线l和⊙O相离 ___________
d>r
d=r
d
例 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,2cm,
2.4cm,3cm为半径画⊙C,斜边AB分别与⊙C有怎样的位置关系?
为什么?
A
B
C
提示:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
直线与圆的位置关系的数量表示
解:过C作CD⊥AB,垂足为D.
在Rt△ABC中,
AB=
5.
由三角形的面积公式,并整理,得
∴
即圆心C到AB的距离d=2.4cm.
当r=2cm时,
d >r,
斜边AB⊙C和相离.
D
当r=2.4cm时,
d =r,
斜边AB⊙C和相切.
当r=3cm时,
d <r,
斜边AB⊙C和相交.
A
B
C
直线与圆的位置关系的数量表示
归纳:一判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 的个数来判断;
(2)由 的大小关系来判断;
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
直线与圆的位置关系的数量表示
练一练:已知⊙O的面积为9π cm2,若点O到直线l的距离为π cm,
则直线l与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
C
CONTENTS
3
随堂练习
1.直线l与半径为r的⊙O相交,且圆心O到直线l的距离为5,则半径r的取值范围是( )
A.r>5
B.r=5
C.0<r<5
D.0<r≤5
A
2.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情况均有可能
C
3.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
C
4.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
B
5.如图,已知∠AOB=30°,M为OA边上一点,以点M为圆心,2 cm为半径作⊙M.若点M在OA边上运动,则OM=_______cm时,⊙M与OB相切.
6.在直角坐标系中,⊙M的圆心坐标是(m,0),半径是2,如果⊙M与y轴所在的直线相切,那么m=_____;如果⊙M与y轴所在的直线相交,那么m的取值范围是____________.
4
±2
-2<m<2
CONTENTS
4
课堂小结
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
1个:相切;
2个:相交
d>r:相离
d=r:相切
d
