31.4 第1课时 用列表法求概率-2021春冀教版九年级数学下册课件(21张PPT)
文档属性
| 名称 | 31.4 第1课时 用列表法求概率-2021春冀教版九年级数学下册课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 464.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:06:37 | ||
图片预览







文档简介
第三十一章 随机事件的概率
31.4 用列举法求简单事件的概率
九年级数学下册冀教版
第1课时 用列表法求概率
1
用列表法求概率
CONTENTS
1
新知导入
想一想:
(1)抛掷两枚骰子,点数总和是5有几种情况;
(2)抛掷两枚骰子,点数总和是6有几种情况;
(3)抛掷两枚骰子,点数总和是8有几种情况;
CONTENTS
2
课程讲授
用列表法求概率
问题1 如图所示,一个质地均匀的正四面体(四个面都是等边三角形),四个面上分别标有数字1,2,3,4.投掷这个正四面体,然后观察底面上的数字.
1.投掷一次,有多少种可能结果?它们发生的可能性相同吗,概率各是多大?
投掷一次,有4种等可能的结果,它们发生的概率都是 .
用列表法求概率
2.投掷两次,共有多少种可能结果?如何表示这些可能结果?
投掷两次,有16(4×4)种等可能的结果,用(m,n)表示两次投掷的结果,其中m为第一次掷出的数,n为第二次掷出的数,m和n分别可能是1,2,3,4.所有可能的结果用表格表示为:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}m n
1
2
3
4
1
(1,1)
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,2)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,3)
(3,4)
4
(4,1)
(4,2)
(4,3)
(4,4)
用列表法求概率
3.如何计算两数之和为2,3,…,8的概率?
{775DCB02-9BB8-47FD-8907-85C794F793BA}+
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
投掷两次,共有16种等可能的结果,事件“两数之和为4”包含3种等可能的结果,分别是(1,3),(2,2),(3,1),所以“两数之和为4”的概率是 .
用列表法求概率
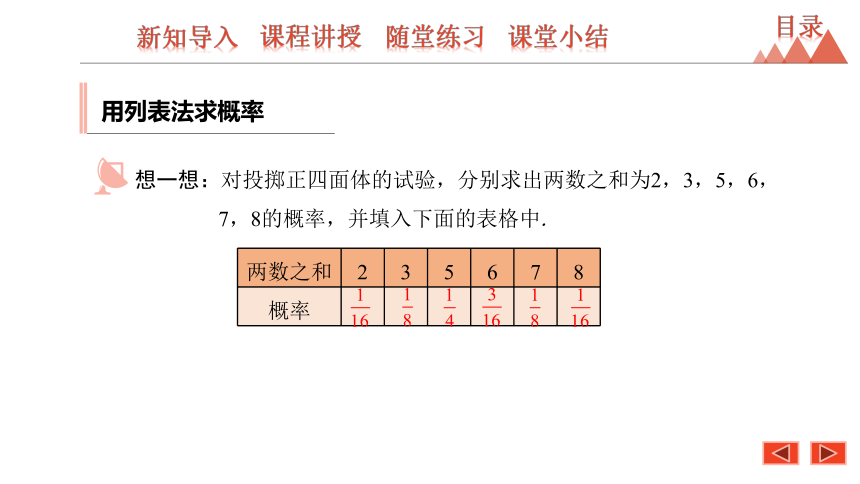
想一想:对投掷正四面体的试验,分别求出两数之和为2,3,5,6,7,8的概率,并填入下面的表格中.
{284E427A-3D55-4303-BF80-6455036E1DE7}两数之和
2
3
5
6
7
8
概率
用列表法求概率
例 如图所示,四个开关按钮中有两个各控制一盏灯,另两个按钮控制一个发音装置.当连续按对两个按钮点亮两盏灯时,“闯关成功”;而只要按错一个按钮,就会发出“闯关失败”的声音.求“闯关成功”的概率.
用列表法求概率
解:不妨设1号,2号按钮各控制一盏灯,连续按两个按钮(不考虑按钮的顺序)的所有可能结果列表如下:
{284E427A-3D55-4303-BF80-6455036E1DE7}按钮代号
12
13
14
23
24
34
结果
成功
失败
失败
失败
失败
失败
所有可能结果有6种,它们都是等可能发生的,而其中只有一种结果为“闯关成功”,所以P(闯关成功)= .
用列表法求概率
归纳:1.列举法求概率的前提:(1)一次试验中,可能出现的结果是有限个;(2)一次试验中,各种结果发生的可能性相等.
2.用列举法求概率的核心是列出各种等可能的结果,所求概率是一个准确数,一般用分数表示.
3.当所有可能的结果较多且烦琐时,用列表的方式能清晰、全面地列出各种可能的结果,且所有结果有规律排列,易于找出某个事件中包含的所有可能性.
4.列表法一般应用于两个元素且结果的可能性较多的题目中.
用列表法求概率
练一练:从-2,-1,2这三个数中任取两个不同的数相乘,积为正数的概率是( )
A.
B.
C.
D.
C
CONTENTS
3
随堂练习
1.从2,3,4中任选两个不同数字组成一个两位数,组成的数是偶数的概率是( )
A.
B.
C.
D.
A
2.一个不透明的袋子中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球,记下标号后放回,再随机摸出一个小球并记下标号,两次摸出的小球标号的和是偶数的概率是( )
A.
B.
C.
D.
D
3.四张背面完全相同的卡片上正面分别印有等腰三角形、平行四边形、菱形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有的图案都是轴对称图形的概率是( )
A.
B.
C.
D.
D
4.现有四张完全相同的卡片,上面分别标有数字-1,-2,3,4.把卡片背面朝上洗匀,然后从中随机抽取两张,则这两张卡片上的数字之积为负数的概率是_____.
3
2
5.有4根细木棒,长度分别为2 cm,3 cm,4 cm,5 cm,从中任选3根,恰好能搭成一个三角形的概率是______.
4
3
6.在一个不透明的袋子里放入除颜色外完全相同的2个红球和2个黄球,摇匀后摸出一个记下颜色,放回后摇匀,再摸出一个,求两次摸出的球均是红球的概率.
解:列表如下:
∴P(两次红球)= .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
红1
红2
黄1
黄2
红1
红1红1
红1红2
红1黄1
红1黄2
红2
红2红1
红2红2
红2黄1
红2黄2
黄1
黄1红1
黄1红2
黄1黄1
黄1黄2
黄2
黄2红1
黄2红2
黄2黄1
黄2黄2
第二次
第一次
CONTENTS
4
课堂小结
用列表法求概率
适合涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多的等可能性事件
31.4 用列举法求简单事件的概率
九年级数学下册冀教版
第1课时 用列表法求概率
1
用列表法求概率
CONTENTS
1
新知导入
想一想:
(1)抛掷两枚骰子,点数总和是5有几种情况;
(2)抛掷两枚骰子,点数总和是6有几种情况;
(3)抛掷两枚骰子,点数总和是8有几种情况;
CONTENTS
2
课程讲授
用列表法求概率
问题1 如图所示,一个质地均匀的正四面体(四个面都是等边三角形),四个面上分别标有数字1,2,3,4.投掷这个正四面体,然后观察底面上的数字.
1.投掷一次,有多少种可能结果?它们发生的可能性相同吗,概率各是多大?
投掷一次,有4种等可能的结果,它们发生的概率都是 .
用列表法求概率
2.投掷两次,共有多少种可能结果?如何表示这些可能结果?
投掷两次,有16(4×4)种等可能的结果,用(m,n)表示两次投掷的结果,其中m为第一次掷出的数,n为第二次掷出的数,m和n分别可能是1,2,3,4.所有可能的结果用表格表示为:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}m n
1
2
3
4
1
(1,1)
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,2)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,3)
(3,4)
4
(4,1)
(4,2)
(4,3)
(4,4)
用列表法求概率
3.如何计算两数之和为2,3,…,8的概率?
{775DCB02-9BB8-47FD-8907-85C794F793BA}+
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
投掷两次,共有16种等可能的结果,事件“两数之和为4”包含3种等可能的结果,分别是(1,3),(2,2),(3,1),所以“两数之和为4”的概率是 .
用列表法求概率
想一想:对投掷正四面体的试验,分别求出两数之和为2,3,5,6,7,8的概率,并填入下面的表格中.
{284E427A-3D55-4303-BF80-6455036E1DE7}两数之和
2
3
5
6
7
8
概率
用列表法求概率
例 如图所示,四个开关按钮中有两个各控制一盏灯,另两个按钮控制一个发音装置.当连续按对两个按钮点亮两盏灯时,“闯关成功”;而只要按错一个按钮,就会发出“闯关失败”的声音.求“闯关成功”的概率.
用列表法求概率
解:不妨设1号,2号按钮各控制一盏灯,连续按两个按钮(不考虑按钮的顺序)的所有可能结果列表如下:
{284E427A-3D55-4303-BF80-6455036E1DE7}按钮代号
12
13
14
23
24
34
结果
成功
失败
失败
失败
失败
失败
所有可能结果有6种,它们都是等可能发生的,而其中只有一种结果为“闯关成功”,所以P(闯关成功)= .
用列表法求概率
归纳:1.列举法求概率的前提:(1)一次试验中,可能出现的结果是有限个;(2)一次试验中,各种结果发生的可能性相等.
2.用列举法求概率的核心是列出各种等可能的结果,所求概率是一个准确数,一般用分数表示.
3.当所有可能的结果较多且烦琐时,用列表的方式能清晰、全面地列出各种可能的结果,且所有结果有规律排列,易于找出某个事件中包含的所有可能性.
4.列表法一般应用于两个元素且结果的可能性较多的题目中.
用列表法求概率
练一练:从-2,-1,2这三个数中任取两个不同的数相乘,积为正数的概率是( )
A.
B.
C.
D.
C
CONTENTS
3
随堂练习
1.从2,3,4中任选两个不同数字组成一个两位数,组成的数是偶数的概率是( )
A.
B.
C.
D.
A
2.一个不透明的袋子中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球,记下标号后放回,再随机摸出一个小球并记下标号,两次摸出的小球标号的和是偶数的概率是( )
A.
B.
C.
D.
D
3.四张背面完全相同的卡片上正面分别印有等腰三角形、平行四边形、菱形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有的图案都是轴对称图形的概率是( )
A.
B.
C.
D.
D
4.现有四张完全相同的卡片,上面分别标有数字-1,-2,3,4.把卡片背面朝上洗匀,然后从中随机抽取两张,则这两张卡片上的数字之积为负数的概率是_____.
3
2
5.有4根细木棒,长度分别为2 cm,3 cm,4 cm,5 cm,从中任选3根,恰好能搭成一个三角形的概率是______.
4
3
6.在一个不透明的袋子里放入除颜色外完全相同的2个红球和2个黄球,摇匀后摸出一个记下颜色,放回后摇匀,再摸出一个,求两次摸出的球均是红球的概率.
解:列表如下:
∴P(两次红球)= .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
红1
红2
黄1
黄2
红1
红1红1
红1红2
红1黄1
红1黄2
红2
红2红1
红2红2
红2黄1
红2黄2
黄1
黄1红1
黄1红2
黄1黄1
黄1黄2
黄2
黄2红1
黄2红2
黄2黄1
黄2黄2
第二次
第一次
CONTENTS
4
课堂小结
用列表法求概率
适合涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多的等可能性事件
