32.2 第1课时 三视图的特点及几何体三视图的画法-2021春冀教版九年级数学下册课件(22张PPT)
文档属性
| 名称 | 32.2 第1课时 三视图的特点及几何体三视图的画法-2021春冀教版九年级数学下册课件(22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览





文档简介
第三十二章 投影与视图
32.2 视 图
九年级数学下册冀教版
第1课时 认识三视图
1
三视图的概念
2
画几何体的三视图
CONTENTS
1
新知导入
想一想:
“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中”.从我们熟悉的这首古诗中,你能得到什么启示?
CONTENTS
2
课程讲授
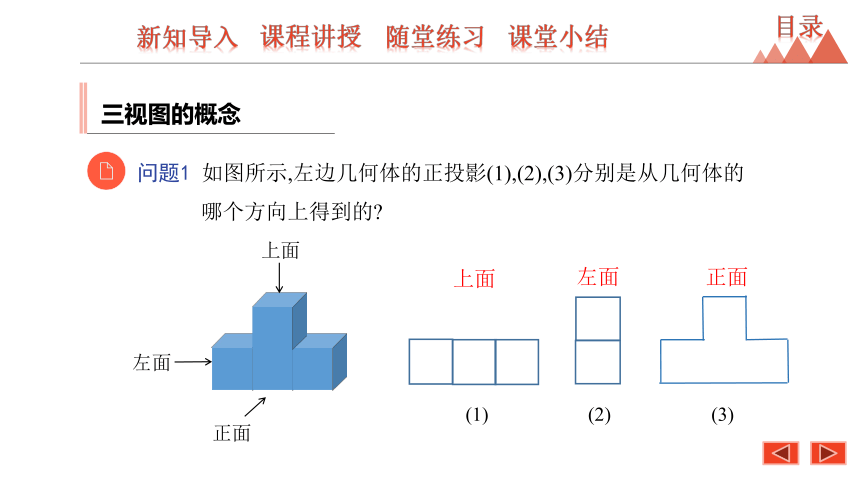
问题1 如图所示,左边几何体的正投影(1),(2),(3)分别是从几何体的哪个方向上得到的?
三视图的概念
左面
正面
上面
(1)
(2)
(3)
上面
左面
正面
三视图的概念
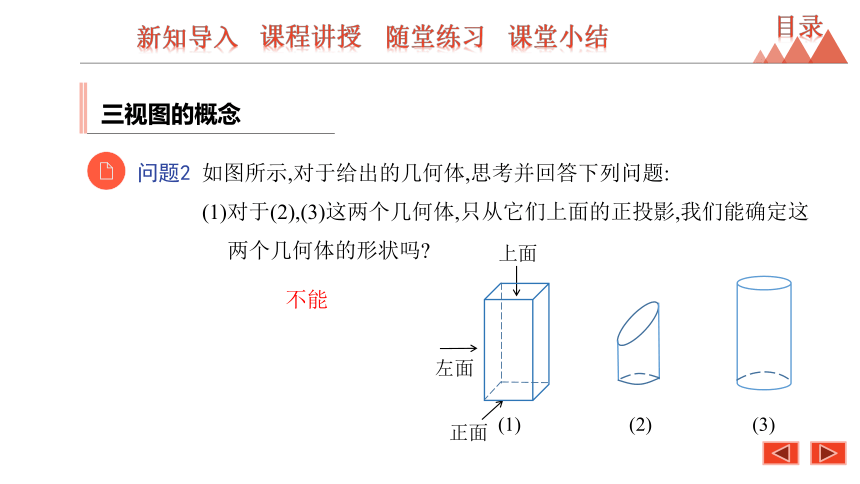
问题2 如图所示,对于给出的几何体,思考并回答下列问题:
(1)对于(2),(3)这两个几何体,只从它们上面的正投影,我们能确定这两个几何体的形状吗?
左面
正面
上面
(1)
(2)
(3)
不能
三视图的概念
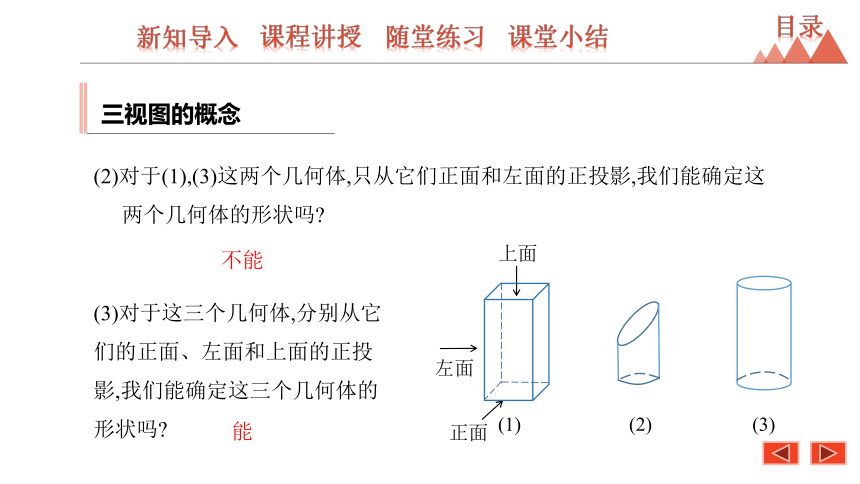
(2)对于(1),(3)这两个几何体,只从它们正面和左面的正投影,我们能确定这两个几何体的形状吗?
不能
左面
正面
上面
(1)
(2)
(3)
(3)对于这三个几何体,分别从它们的正面、左面和上面的正投影,我们能确定这三个几何体的形状吗?
能
三视图的概念
定义:一个几何体的正投影,又叫做这个几何体的视图.从正面得到的视图叫做主视图,从上面得到的视图叫做俯视图,从左面得到的视图叫做左视图.
三视图的概念
我们约定面对几何体的一面为几何体的正面,由左向右方向的一面为几何体的左面,竖直向下方向的一面为几何体的上面.
如图(1)所示的这个几何体的主视图、俯视图和左视图如图(2)所示.
画几何体的三视图
例 画出如图所示的圆柱的主视图、俯视图和左视图.
解:如图所示.
画几何体的三视图
想一想:(1)圆柱的主视图中长方形的长和宽与圆柱之间有什么关系?
(2)圆柱的左视图中长方形的长和宽与圆柱之间有什么关系?
(3)圆柱的俯视图中圆与圆柱之间有什么关系?
(4)你能归纳画一个几何体的三视图的一般步骤吗?
圆柱的主视图是一个长方形,长方形的长和宽分别等于圆柱的高和圆柱底面圆的直径;它的俯视图是一个圆,圆的直径等于圆柱底面圆的直径;它的左视图也是一个长方形,长方形的长和宽分别等于圆柱的高和圆柱底面圆的直径.
画几何体的三视图
归纳:画几何体的三视图的步骤:
(1)确定主视图的位置,画出主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正”.
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
画几何体的三视图
练一练:如图所示,请画出球的主视图、俯视图和左视图.
主视图
俯视图
左视图
画几何体的三视图
归纳:1.三个视图分别从不同方向表示物体的形状,单独一个视图难以全面地反映物体的形状,三者合起来才能较全面地反映物体的形状.
2.对于同一个物体,观察的角度不同,所得到的视图也不同.
3.俯视图在主视图的下方,左视图在主视图的右边,画三视图时,三个视图要放在正确的位置,不能随意乱放.三视图之间要保证“长对正、高平齐、宽相等”,这三个关系是看图与画图的基本规律.一般情况下,一个视图不能确定物体的空间形状,看图时必须将各视图对照起来看,这样才能看清物体的全貌.
CONTENTS
3
随堂练习
1.如图,该几何体的俯视图是( )
A
2.(2016·漳州中考)下列几何体中,左视图为圆的是( )
A
B
C
D
C
3.在①长方体、②球、③圆锥、④圆柱这四种几何体中,其主视图、左视图、俯视图都完全相同的是 .(填序号)?
②
4.画出如图所示的一些基本几何体的三视图.
解:三视图如图所示.
主视图
左视图
俯视图
主视图
左视图
俯视图
CONTENTS
4
课堂小结
三视图
几何体的三视图
三视图的画法
主视图
俯视图
左视图
1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图长对正;
3. 在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
32.2 视 图
九年级数学下册冀教版
第1课时 认识三视图
1
三视图的概念
2
画几何体的三视图
CONTENTS
1
新知导入
想一想:
“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中”.从我们熟悉的这首古诗中,你能得到什么启示?
CONTENTS
2
课程讲授
问题1 如图所示,左边几何体的正投影(1),(2),(3)分别是从几何体的哪个方向上得到的?
三视图的概念
左面
正面
上面
(1)
(2)
(3)
上面
左面
正面
三视图的概念
问题2 如图所示,对于给出的几何体,思考并回答下列问题:
(1)对于(2),(3)这两个几何体,只从它们上面的正投影,我们能确定这两个几何体的形状吗?
左面
正面
上面
(1)
(2)
(3)
不能
三视图的概念
(2)对于(1),(3)这两个几何体,只从它们正面和左面的正投影,我们能确定这两个几何体的形状吗?
不能
左面
正面
上面
(1)
(2)
(3)
(3)对于这三个几何体,分别从它们的正面、左面和上面的正投影,我们能确定这三个几何体的形状吗?
能
三视图的概念
定义:一个几何体的正投影,又叫做这个几何体的视图.从正面得到的视图叫做主视图,从上面得到的视图叫做俯视图,从左面得到的视图叫做左视图.
三视图的概念
我们约定面对几何体的一面为几何体的正面,由左向右方向的一面为几何体的左面,竖直向下方向的一面为几何体的上面.
如图(1)所示的这个几何体的主视图、俯视图和左视图如图(2)所示.
画几何体的三视图
例 画出如图所示的圆柱的主视图、俯视图和左视图.
解:如图所示.
画几何体的三视图
想一想:(1)圆柱的主视图中长方形的长和宽与圆柱之间有什么关系?
(2)圆柱的左视图中长方形的长和宽与圆柱之间有什么关系?
(3)圆柱的俯视图中圆与圆柱之间有什么关系?
(4)你能归纳画一个几何体的三视图的一般步骤吗?
圆柱的主视图是一个长方形,长方形的长和宽分别等于圆柱的高和圆柱底面圆的直径;它的俯视图是一个圆,圆的直径等于圆柱底面圆的直径;它的左视图也是一个长方形,长方形的长和宽分别等于圆柱的高和圆柱底面圆的直径.
画几何体的三视图
归纳:画几何体的三视图的步骤:
(1)确定主视图的位置,画出主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正”.
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
画几何体的三视图
练一练:如图所示,请画出球的主视图、俯视图和左视图.
主视图
俯视图
左视图
画几何体的三视图
归纳:1.三个视图分别从不同方向表示物体的形状,单独一个视图难以全面地反映物体的形状,三者合起来才能较全面地反映物体的形状.
2.对于同一个物体,观察的角度不同,所得到的视图也不同.
3.俯视图在主视图的下方,左视图在主视图的右边,画三视图时,三个视图要放在正确的位置,不能随意乱放.三视图之间要保证“长对正、高平齐、宽相等”,这三个关系是看图与画图的基本规律.一般情况下,一个视图不能确定物体的空间形状,看图时必须将各视图对照起来看,这样才能看清物体的全貌.
CONTENTS
3
随堂练习
1.如图,该几何体的俯视图是( )
A
2.(2016·漳州中考)下列几何体中,左视图为圆的是( )
A
B
C
D
C
3.在①长方体、②球、③圆锥、④圆柱这四种几何体中,其主视图、左视图、俯视图都完全相同的是 .(填序号)?
②
4.画出如图所示的一些基本几何体的三视图.
解:三视图如图所示.
主视图
左视图
俯视图
主视图
左视图
俯视图
CONTENTS
4
课堂小结
三视图
几何体的三视图
三视图的画法
主视图
俯视图
左视图
1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图长对正;
3. 在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
