32.2 第3课时 根据三视图描述几何体的形状与有关计算-2021春冀教版九年级数学下册课件(26张PPT)
文档属性
| 名称 | 32.2 第3课时 根据三视图描述几何体的形状与有关计算-2021春冀教版九年级数学下册课件(26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 783.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览




文档简介
第三十二章 投影与视图
32.2 视 图
九年级数学下册冀教版
第3课时 根据三视图描述几何体的形状与有关计算
1
由三视图确定几何体
2
由三视图求几何体的表面积或体积
CONTENTS
1
新知导入
想一想:
请将下列帖子贴在正方体对应的位置上
右面
正面
上面
CONTENTS
2
课程讲授
由三视图确定几何体
问题1 如图所示,根据视图,分别描述相应几何体的形状.
解:图中主视图和左视图是长方形,所以该几何体是柱体,图(1)的俯视图是圆,所以图(1)的几何体是圆柱;
图(2)的俯视图是正方形,所以图(2)的几何体是长方体.
由三视图确定几何体
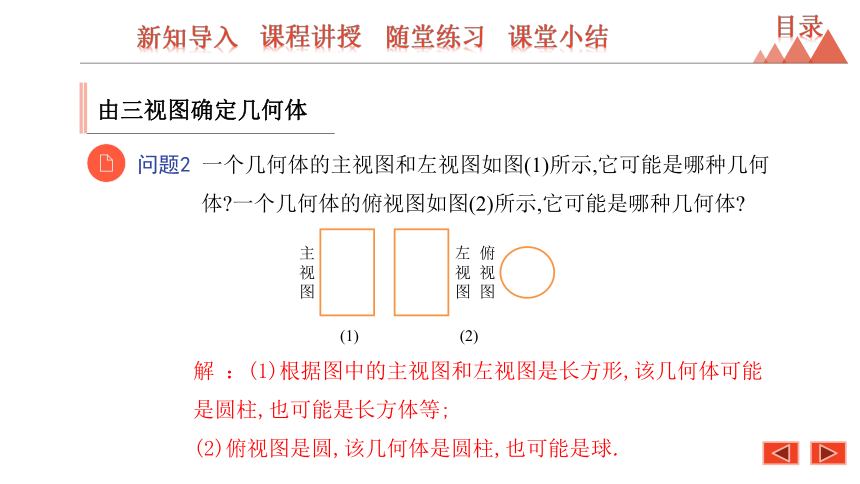
问题2 一个几何体的主视图和左视图如图(1)所示,它可能是哪种几何体?一个几何体的俯视图如图(2)所示,它可能是哪种几何体?
解 :(1)根据图中的主视图和左视图是长方形,该几何体可能是圆柱,也可能是长方体等;
(2)俯视图是圆,该几何体是圆柱,也可能是球.
主视图
左视图
俯视图
(1) (2)
由三视图确定几何体
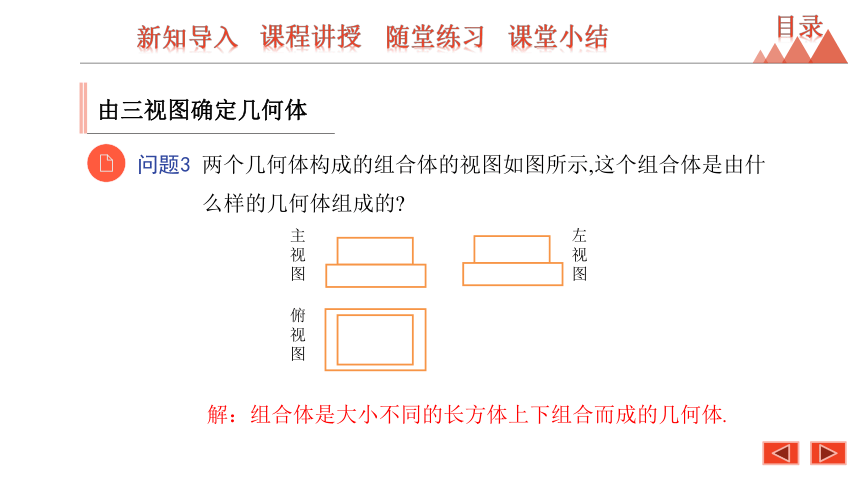
问题3 两个几何体构成的组合体的视图如图所示,这个组合体是由什么样的几何体组成的?
解:组合体是大小不同的长方体上下组合而成的几何体.
主视图
左视图
俯视图
由三视图确定几何体
归纳:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左面,然后再综合起来考虑整体图形.
由三视图确定几何体
例 如图所示,图(1)、图(2)、图(3)分别是底面为正三角形、等腰直角三角形的三棱柱和底面为正方形的四棱柱的俯视图,分别画出它们的主视图和左视图.(棱柱的高都是1.6 cm)
由三视图确定几何体
解:如图所示.
由三视图确定几何体
归纳:1.由一个视图不能确定物体的空间形状,根据三视图描述几何体或实物原型时,必须将各视图对照起来看.
2.一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性.例如:正放的正方体的主视图是正方形,但主视图是正方形的几何体有直三棱柱、长方体、圆柱等.
3.三视图是平面图形,它是平行光线从不同方向照射物体所得的投影,并且平行光线和投影面是垂直的.
由三视图确定几何体
练一练:如图所示的是某个几何体的三视图,该几何体是( )
A.圆锥
B.三棱锥
C.圆柱
D.三棱柱
D
20cm
32cm
30cm
25cm
40cm
主视图
俯视图
左视图
由三视图求几何体的表面积或体积
例1 如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
提示:由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积,然后相加即可.
解:该图形上、下部分分别是圆柱、长方体,如下图所示.
由三视图求几何体的表面积或体积
20×32π+30×40×2+25×40×2+25×30×2
表面积为
=(5 900+640π)(cm2),
=(30 000+3 200π)(cm3).
体积为
25×30×40+102×32π
由三视图求几何体的表面积或体积
归纳:由三视图求几何体的表面积或体积的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;
(2) 根据已知数据,求出立体图形的表面积或体积.
C
由三视图求几何体的表面积或体积
练一练:如图是一个几何体的三视图(尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是( )
A.12 cm2
B.(12+π)cm2
C.6π cm2
D.8π cm2
CONTENTS
3
随堂练习
1.如图是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
D
2.一个几何体的三视图如图所示,则这个几何体是( )
C
3.如图是下列哪个几何体的主视图与俯视图( )
C
4. 一个几何体的三视图如图所示,则该几何体的表面积是( )
A.24+2π
B.16+4π
C.16+8π
D.16+12π
D
5.下图是某几何体的展开图.
(1)这个几何体的名称是__________;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(π取3.14)
圆柱
主视图
俯视图
左视图
解:(2)三视图如右图.
(3)V圆柱=πr2h
=3.14×52×20
=1570(cm2).
CONTENTS
4
课堂小结
由三视图还原几何图形
一般类型
基本方法
由三视图确定简单几何图形
由三视图确定复杂几何图形
根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
计算几何体的表面积和体积
根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等数据
根据已知数据,求出立体图形的体积或表面积.
32.2 视 图
九年级数学下册冀教版
第3课时 根据三视图描述几何体的形状与有关计算
1
由三视图确定几何体
2
由三视图求几何体的表面积或体积
CONTENTS
1
新知导入
想一想:
请将下列帖子贴在正方体对应的位置上
右面
正面
上面
CONTENTS
2
课程讲授
由三视图确定几何体
问题1 如图所示,根据视图,分别描述相应几何体的形状.
解:图中主视图和左视图是长方形,所以该几何体是柱体,图(1)的俯视图是圆,所以图(1)的几何体是圆柱;
图(2)的俯视图是正方形,所以图(2)的几何体是长方体.
由三视图确定几何体
问题2 一个几何体的主视图和左视图如图(1)所示,它可能是哪种几何体?一个几何体的俯视图如图(2)所示,它可能是哪种几何体?
解 :(1)根据图中的主视图和左视图是长方形,该几何体可能是圆柱,也可能是长方体等;
(2)俯视图是圆,该几何体是圆柱,也可能是球.
主视图
左视图
俯视图
(1) (2)
由三视图确定几何体
问题3 两个几何体构成的组合体的视图如图所示,这个组合体是由什么样的几何体组成的?
解:组合体是大小不同的长方体上下组合而成的几何体.
主视图
左视图
俯视图
由三视图确定几何体
归纳:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左面,然后再综合起来考虑整体图形.
由三视图确定几何体
例 如图所示,图(1)、图(2)、图(3)分别是底面为正三角形、等腰直角三角形的三棱柱和底面为正方形的四棱柱的俯视图,分别画出它们的主视图和左视图.(棱柱的高都是1.6 cm)
由三视图确定几何体
解:如图所示.
由三视图确定几何体
归纳:1.由一个视图不能确定物体的空间形状,根据三视图描述几何体或实物原型时,必须将各视图对照起来看.
2.一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性.例如:正放的正方体的主视图是正方形,但主视图是正方形的几何体有直三棱柱、长方体、圆柱等.
3.三视图是平面图形,它是平行光线从不同方向照射物体所得的投影,并且平行光线和投影面是垂直的.
由三视图确定几何体
练一练:如图所示的是某个几何体的三视图,该几何体是( )
A.圆锥
B.三棱锥
C.圆柱
D.三棱柱
D
20cm
32cm
30cm
25cm
40cm
主视图
俯视图
左视图
由三视图求几何体的表面积或体积
例1 如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
提示:由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积,然后相加即可.
解:该图形上、下部分分别是圆柱、长方体,如下图所示.
由三视图求几何体的表面积或体积
20×32π+30×40×2+25×40×2+25×30×2
表面积为
=(5 900+640π)(cm2),
=(30 000+3 200π)(cm3).
体积为
25×30×40+102×32π
由三视图求几何体的表面积或体积
归纳:由三视图求几何体的表面积或体积的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;
(2) 根据已知数据,求出立体图形的表面积或体积.
C
由三视图求几何体的表面积或体积
练一练:如图是一个几何体的三视图(尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是( )
A.12 cm2
B.(12+π)cm2
C.6π cm2
D.8π cm2
CONTENTS
3
随堂练习
1.如图是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
D
2.一个几何体的三视图如图所示,则这个几何体是( )
C
3.如图是下列哪个几何体的主视图与俯视图( )
C
4. 一个几何体的三视图如图所示,则该几何体的表面积是( )
A.24+2π
B.16+4π
C.16+8π
D.16+12π
D
5.下图是某几何体的展开图.
(1)这个几何体的名称是__________;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(π取3.14)
圆柱
主视图
俯视图
左视图
解:(2)三视图如右图.
(3)V圆柱=πr2h
=3.14×52×20
=1570(cm2).
CONTENTS
4
课堂小结
由三视图还原几何图形
一般类型
基本方法
由三视图确定简单几何图形
由三视图确定复杂几何图形
根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
计算几何体的表面积和体积
根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等数据
根据已知数据,求出立体图形的体积或表面积.
