华东师大版 九年级下 26.2.1函数y=ax^2的图象与性质课件(共15张)
文档属性
| 名称 | 华东师大版 九年级下 26.2.1函数y=ax^2的图象与性质课件(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 584.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:12:32 | ||
图片预览





文档简介
二次函数y=ax2的图象和性质
复习巩固
1.什么是二次函数? 2.二次函数有哪些特征?
3.判断哪些是二次函数:(1)y=3x-1 (2)y=ax2+bx+c (3)y=x2+1/x (4)s=2t2-2t+1 (5)y=(x-1)2-x2
4.若 是二次函数,则a=____
5.某商场购进一种单价为40元的商品,如果以单价60元卖出,那么每天可以卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x元,每天销售y个,每天获利W元:(1)写出y与x的函数关系式_______
(2)求出W与x的函数关系式__________________
探究一:函数y=x2的图象与性质
1.利用描点法作图:
x
y=x2
...
-3
-2
-1
0
1
2
3
...
…
9
4
1
0
1
4
9
…
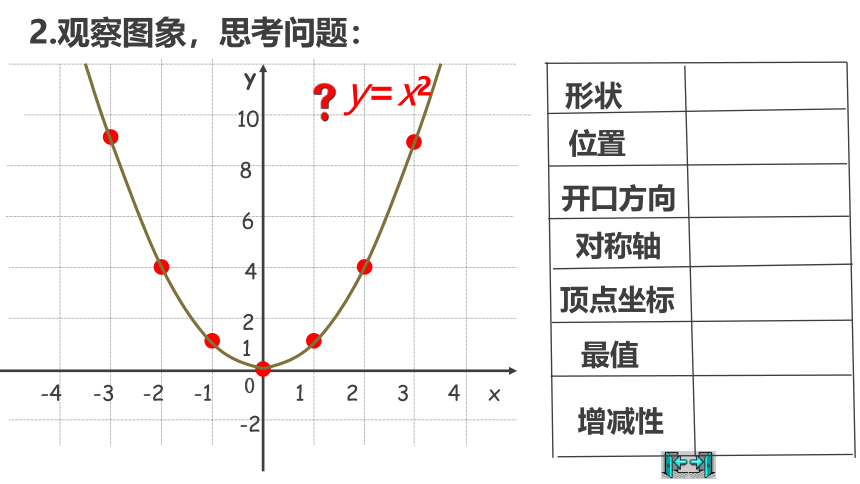
2.观察图象,思考问题:
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
1
y=x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
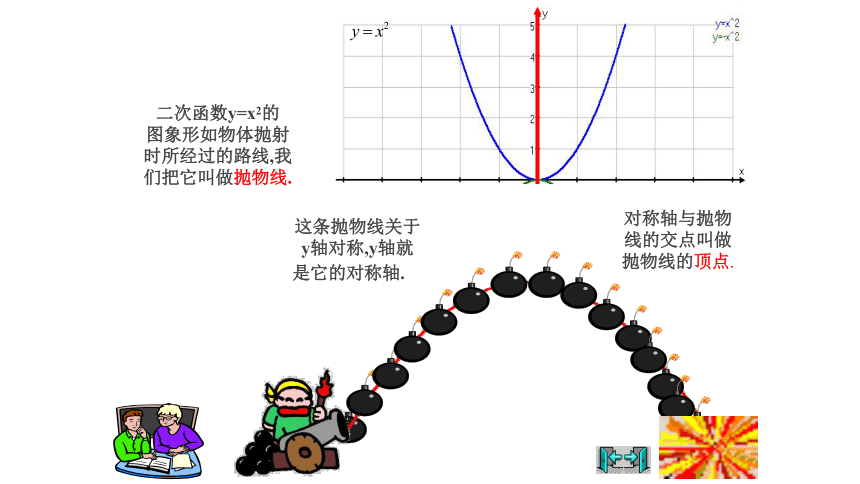
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
二次函数y=x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.
3.得出结论:
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}函数
y=x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
抛物线
除顶点外,图象位于x轴的上方
开口向上
y轴
(0,0)
当x=0时,y有最小值为0
当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大
探究二:函数y=-x2的图象与性质
1.利用描点法作图:
x
y=-x2
...
-3
-2
-1
0
1
2
3
...
…
-9
-4
-1
0
-1
-4
-9
…
x
y
0
-4
-3
-2
-1
1
2
3
4
-10
-8
-6
-4
-2
2
-1
观察图象,思考问题:
y=-x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
3.得出结论:
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}函数
y=-x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
抛物线
除顶点外,图象位于x轴的下方
开口向下
y轴
(0,0)
当x=0时,y有最大值为0
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小
探究三:y=x2 与y=-x2图象的异同
思考:y=x2 与y=-x2图象有什么共同点?又有什么区别呢?
共同点:
都是抛物线、都关于y轴对称,顶点坐标都为(0,0)
不同点:
开口方向不同、位置不同、增减性不同、最值不同
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}函数
y=ax2
a
位置
开口方向
对称轴
顶点坐标
最值
增减性
探究四:归纳y=ax2的性质
a>0
a<0
除顶点外,位于x轴上方
除顶点外,位于x轴下方
开口向上
开口向下
y轴
y轴
(0,0)
(0,0)
当x=0时,y有最小值为0
当x=0时,y有最大值为0
x<0,y随x的增大而减小;
x>0,y随x的增大而增大
x<0,y随x的增大而增大;
x>0,y随x的增大而减小
典例精讲
1.已知二次函数y=ax2(a≠0)的图象经过点(-2,-3):
(1)求a的值,并写出这个二次函数的表达式;
(2)说出这个函数的顶点坐标,开口方向等性质。
2.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).
典例精讲
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
典例精讲
3.对于函数y=4x2
(1)说出图象的开口方向,对称轴,顶点坐标,增减性;
(2)若A(x1,y1),B(x2,y2)都在该函数图象上,且x1>x2>0,比较
y1与y2的大小关系。
当堂检测
1.教材第7页,练习第2、3题
2.《课堂10分钟》
复习巩固
1.什么是二次函数? 2.二次函数有哪些特征?
3.判断哪些是二次函数:(1)y=3x-1 (2)y=ax2+bx+c (3)y=x2+1/x (4)s=2t2-2t+1 (5)y=(x-1)2-x2
4.若 是二次函数,则a=____
5.某商场购进一种单价为40元的商品,如果以单价60元卖出,那么每天可以卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x元,每天销售y个,每天获利W元:(1)写出y与x的函数关系式_______
(2)求出W与x的函数关系式__________________
探究一:函数y=x2的图象与性质
1.利用描点法作图:
x
y=x2
...
-3
-2
-1
0
1
2
3
...
…
9
4
1
0
1
4
9
…
2.观察图象,思考问题:
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
1
y=x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
二次函数y=x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.
3.得出结论:
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}函数
y=x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
抛物线
除顶点外,图象位于x轴的上方
开口向上
y轴
(0,0)
当x=0时,y有最小值为0
当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大
探究二:函数y=-x2的图象与性质
1.利用描点法作图:
x
y=-x2
...
-3
-2
-1
0
1
2
3
...
…
-9
-4
-1
0
-1
-4
-9
…
x
y
0
-4
-3
-2
-1
1
2
3
4
-10
-8
-6
-4
-2
2
-1
观察图象,思考问题:
y=-x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
3.得出结论:
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}函数
y=-x2
形状
位置
开口方向
对称轴
顶点坐标
最值
增减性
抛物线
除顶点外,图象位于x轴的下方
开口向下
y轴
(0,0)
当x=0时,y有最大值为0
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小
探究三:y=x2 与y=-x2图象的异同
思考:y=x2 与y=-x2图象有什么共同点?又有什么区别呢?
共同点:
都是抛物线、都关于y轴对称,顶点坐标都为(0,0)
不同点:
开口方向不同、位置不同、增减性不同、最值不同
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}函数
y=ax2
a
位置
开口方向
对称轴
顶点坐标
最值
增减性
探究四:归纳y=ax2的性质
a>0
a<0
除顶点外,位于x轴上方
除顶点外,位于x轴下方
开口向上
开口向下
y轴
y轴
(0,0)
(0,0)
当x=0时,y有最小值为0
当x=0时,y有最大值为0
x<0,y随x的增大而减小;
x>0,y随x的增大而增大
x<0,y随x的增大而增大;
x>0,y随x的增大而减小
典例精讲
1.已知二次函数y=ax2(a≠0)的图象经过点(-2,-3):
(1)求a的值,并写出这个二次函数的表达式;
(2)说出这个函数的顶点坐标,开口方向等性质。
2.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).
典例精讲
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
典例精讲
3.对于函数y=4x2
(1)说出图象的开口方向,对称轴,顶点坐标,增减性;
(2)若A(x1,y1),B(x2,y2)都在该函数图象上,且x1>x2>0,比较
y1与y2的大小关系。
当堂检测
1.教材第7页,练习第2、3题
2.《课堂10分钟》
