华东师大版七年级数学下册课件:6.3 第1课时 物体形状变化问题(共15张)
文档属性
| 名称 | 华东师大版七年级数学下册课件:6.3 第1课时 物体形状变化问题(共15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:15:48 | ||
图片预览








文档简介
第6章 一元一次方程
6.3 第1课时 物体形状变化问题
情景导入
h
R
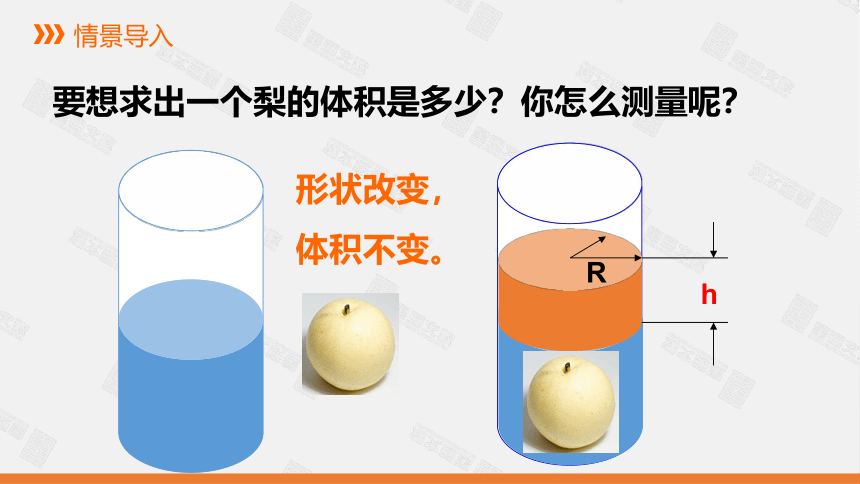
要想求出一个梨的体积是多少?你怎么测量呢?
形状改变,
体积不变。
获取新知
问题1
用一根长60厘米的铁丝围成一个长方形.
(1) 如果长方形的宽是长的 求这个长方形的长和宽;
(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
(3)比较(1)、(2)所得的两个长方形面积的大小. 还能围出
面积更大的长方形吗?
[探究1] 等长变化
每小题中如何设未知数?在小题(2)中,能不能直接设长方形的面积为x平方厘米?若不能,该怎么办?
讨论
(3)当长方形的长为18厘米,宽为12厘米时.
长方形的面积=18×12=216(平方厘米).
当长方形的长为17厘米,宽为13厘米时.
长方形的面积=221(平方厘米).
∴(1)中的长方形面积比(2)中的长方形面积小.
将小题(2)中的宽比长少4厘米改为少3厘米、2厘米、1厘米、0厘米(即长与宽相等),长方形的面积分别 有什么变化?
探索
等长变形是指将物体(通常指铁丝等)围成不同的图形,
图形的形状、面积发生了变化,但周长不变,可抓住周长不
变列出方程.
常见几何体的周长和面积公式有:
长方形的周长=2×(长+宽),长方形的面积=长×宽;
正方形的周长=4×边长,正方形的面积=边长×边长;
三角形的面积= ×底×高;
平行四边形的面积=底×高;
梯形的面积= ×(上底+下底)×高.
例题讲解
例1 用一根长为10米的铁丝围成一个长方形.
(1)若该长方形的长比宽多1.4米.此时长方形的长和宽各为多少米?
(2)若该长方形的长比宽多0.8米,此时长方形的长和宽各为多少米?它围成的长方形的面积与(1)中所围成长方形相比,有什么变化?
(3)若该长方形的长与宽相等,即围成一个正方形,那么正方形的边长是多少?它围成的长方形的面积与(2)中长方形相比,又有什么变化?
解:(1)设此时长方形的宽为x米,则它的长为(x+1.4)米,
根据题意,得[x+(x+1.4)]×2=10,
2x=5-1.4,
2x=3.6,
x=1.8,
x+1.4=1.8+1.4=3.2.
答:此长方形的长和宽分别为3.2米、1.8米.
(2)设此时长方形的宽为x米,则它的长为(x+0.8)米,
根据题意,得[x+(x+0.8)]×2=10,
2x=5-0.8,
2x=4.2,
x=2.1,
x+0.8=2.1+0.8=2.9.
即长方形的长和宽分别是2.9米和2.1米.
此时面积为2.1×2.9=6.09(平方米).(1)中长方形面积为3.2×1.8=5.76(平方米).
6.09-5.76=0.33(平方米).
即比(1)中长方形面积增大0.33平方米.
(3)设正方形的边长为x米.
根据题意得4x=10,x=2.5,
面积为2.5×2.5=6.25(平方米).6.25-6.09=0.16(平方米).
即比(2)中面积增大0.16平方米.
此类问题解答题目的关键是无论图形如何变化,
图形的周长不变.
某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的
前提下,水箱的高度应由
原先的4 m增高为多少米?
[探究2]等积变化
【解析】
如果设水箱的高变为x m,则
{8A107856-5554-42FB-B03E-39F5DBC370BA}?
旧水箱
新水箱
底面半径/m
2
1.6
高/m
4
x
体积/m3
π×22×4
π×1.62×x
等积变形指图形或物体的形状发生变化,但变化前后的体积或面积不变.等积变形问题中的等量关系是:变化前图形或物体的体积(面积)=变化后图形或物体的体积(面积).
随堂演练
1.一根细绳可围成边长为7 cm的正方形,若将此细绳改围成长比宽大2 cm的长方形,则该长方形的长、宽分别是多少厘米?
解:设长方形的长为x cm,则宽为(x-2)cm.
根据题意,得2x+2(x-2)=4×7,
解得x=8.
∴x-2=6.
答:该长方形的长是8 cm,宽是6 cm.
2.如图所示,小明将一张正方形纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
解:设该正方形的边长为x厘米.
由题意,得4x=5(x-4),
解得x=20.
4x=80.
答:每一个长条的面积是80平方厘米.
3.某车间要锻造直径为40毫米,高为45毫米的圆柱形零件毛坯,需截取直径为30毫米的圆钢多长?
根据题意,得π× ×45=π× ·x.
整理,得400×45=152·x.
解得x=80.
答:需截取直径为30毫米的圆钢80毫米.
解:设需截取直径为30毫米的圆钢x毫米.
40 2
( — )
2
30 2
( — )
2
课堂小结
1.“等积变形”是以形状改变而体积不变为前提,常用的关系有:
(1)形状变了,体积没变;
(2)原材料体积=成品体积.
2.解决等积变形的问题时,通常利用体积相等建立方程.
6.3 第1课时 物体形状变化问题
情景导入
h
R
要想求出一个梨的体积是多少?你怎么测量呢?
形状改变,
体积不变。
获取新知
问题1
用一根长60厘米的铁丝围成一个长方形.
(1) 如果长方形的宽是长的 求这个长方形的长和宽;
(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
(3)比较(1)、(2)所得的两个长方形面积的大小. 还能围出
面积更大的长方形吗?
[探究1] 等长变化
每小题中如何设未知数?在小题(2)中,能不能直接设长方形的面积为x平方厘米?若不能,该怎么办?
讨论
(3)当长方形的长为18厘米,宽为12厘米时.
长方形的面积=18×12=216(平方厘米).
当长方形的长为17厘米,宽为13厘米时.
长方形的面积=221(平方厘米).
∴(1)中的长方形面积比(2)中的长方形面积小.
将小题(2)中的宽比长少4厘米改为少3厘米、2厘米、1厘米、0厘米(即长与宽相等),长方形的面积分别 有什么变化?
探索
等长变形是指将物体(通常指铁丝等)围成不同的图形,
图形的形状、面积发生了变化,但周长不变,可抓住周长不
变列出方程.
常见几何体的周长和面积公式有:
长方形的周长=2×(长+宽),长方形的面积=长×宽;
正方形的周长=4×边长,正方形的面积=边长×边长;
三角形的面积= ×底×高;
平行四边形的面积=底×高;
梯形的面积= ×(上底+下底)×高.
例题讲解
例1 用一根长为10米的铁丝围成一个长方形.
(1)若该长方形的长比宽多1.4米.此时长方形的长和宽各为多少米?
(2)若该长方形的长比宽多0.8米,此时长方形的长和宽各为多少米?它围成的长方形的面积与(1)中所围成长方形相比,有什么变化?
(3)若该长方形的长与宽相等,即围成一个正方形,那么正方形的边长是多少?它围成的长方形的面积与(2)中长方形相比,又有什么变化?
解:(1)设此时长方形的宽为x米,则它的长为(x+1.4)米,
根据题意,得[x+(x+1.4)]×2=10,
2x=5-1.4,
2x=3.6,
x=1.8,
x+1.4=1.8+1.4=3.2.
答:此长方形的长和宽分别为3.2米、1.8米.
(2)设此时长方形的宽为x米,则它的长为(x+0.8)米,
根据题意,得[x+(x+0.8)]×2=10,
2x=5-0.8,
2x=4.2,
x=2.1,
x+0.8=2.1+0.8=2.9.
即长方形的长和宽分别是2.9米和2.1米.
此时面积为2.1×2.9=6.09(平方米).(1)中长方形面积为3.2×1.8=5.76(平方米).
6.09-5.76=0.33(平方米).
即比(1)中长方形面积增大0.33平方米.
(3)设正方形的边长为x米.
根据题意得4x=10,x=2.5,
面积为2.5×2.5=6.25(平方米).6.25-6.09=0.16(平方米).
即比(2)中面积增大0.16平方米.
此类问题解答题目的关键是无论图形如何变化,
图形的周长不变.
某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的
前提下,水箱的高度应由
原先的4 m增高为多少米?
[探究2]等积变化
【解析】
如果设水箱的高变为x m,则
{8A107856-5554-42FB-B03E-39F5DBC370BA}?
旧水箱
新水箱
底面半径/m
2
1.6
高/m
4
x
体积/m3
π×22×4
π×1.62×x
等积变形指图形或物体的形状发生变化,但变化前后的体积或面积不变.等积变形问题中的等量关系是:变化前图形或物体的体积(面积)=变化后图形或物体的体积(面积).
随堂演练
1.一根细绳可围成边长为7 cm的正方形,若将此细绳改围成长比宽大2 cm的长方形,则该长方形的长、宽分别是多少厘米?
解:设长方形的长为x cm,则宽为(x-2)cm.
根据题意,得2x+2(x-2)=4×7,
解得x=8.
∴x-2=6.
答:该长方形的长是8 cm,宽是6 cm.
2.如图所示,小明将一张正方形纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
解:设该正方形的边长为x厘米.
由题意,得4x=5(x-4),
解得x=20.
4x=80.
答:每一个长条的面积是80平方厘米.
3.某车间要锻造直径为40毫米,高为45毫米的圆柱形零件毛坯,需截取直径为30毫米的圆钢多长?
根据题意,得π× ×45=π× ·x.
整理,得400×45=152·x.
解得x=80.
答:需截取直径为30毫米的圆钢80毫米.
解:设需截取直径为30毫米的圆钢x毫米.
40 2
( — )
2
30 2
( — )
2
课堂小结
1.“等积变形”是以形状改变而体积不变为前提,常用的关系有:
(1)形状变了,体积没变;
(2)原材料体积=成品体积.
2.解决等积变形的问题时,通常利用体积相等建立方程.
