冀教版初中数学九年级上册26.3 解直角三角形课件 (1)(19张ppt)
文档属性
| 名称 | 冀教版初中数学九年级上册26.3 解直角三角形课件 (1)(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 854.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览





文档简介
解直角三角形
复习旧知
1 什么是锐角三角函数?
2 我们计算锐角三角函数时都是在 什么条件下求值?
3 正切,正弦,余弦三角函数的边和角之间都有什么关系?
4
三角函数值
30°
45°
60°
sin
cos
tan
解直角三角形
学习目标:
1、理解解直角三角形的概念
2、会根据三角形中的已知量正确地求未知量
3、体会数学中的“化归” 思想
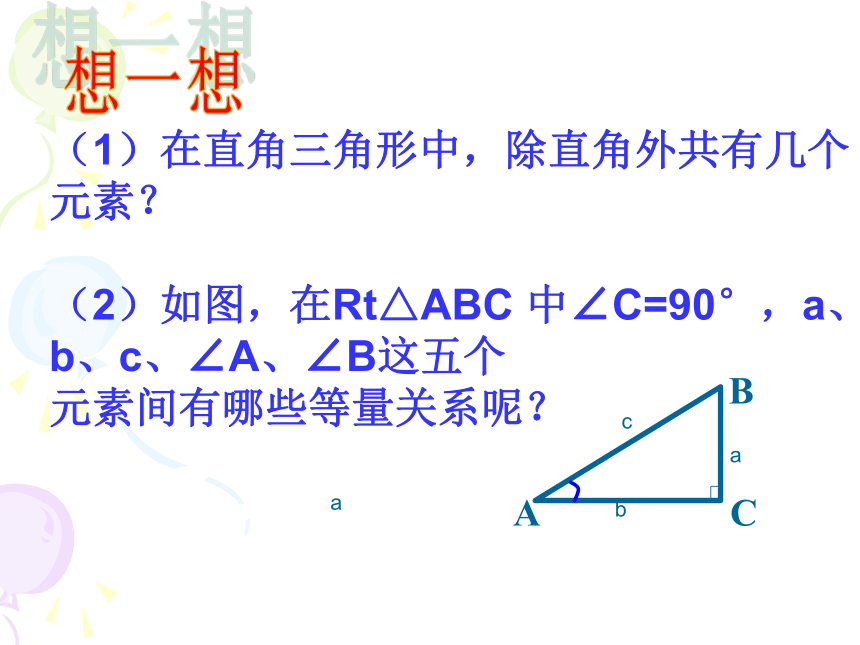
(1)在直角三角形中,除直角外共有几个 元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个
元素间有哪些等量关系呢?
A
B
C
a
c
b
a
想一想
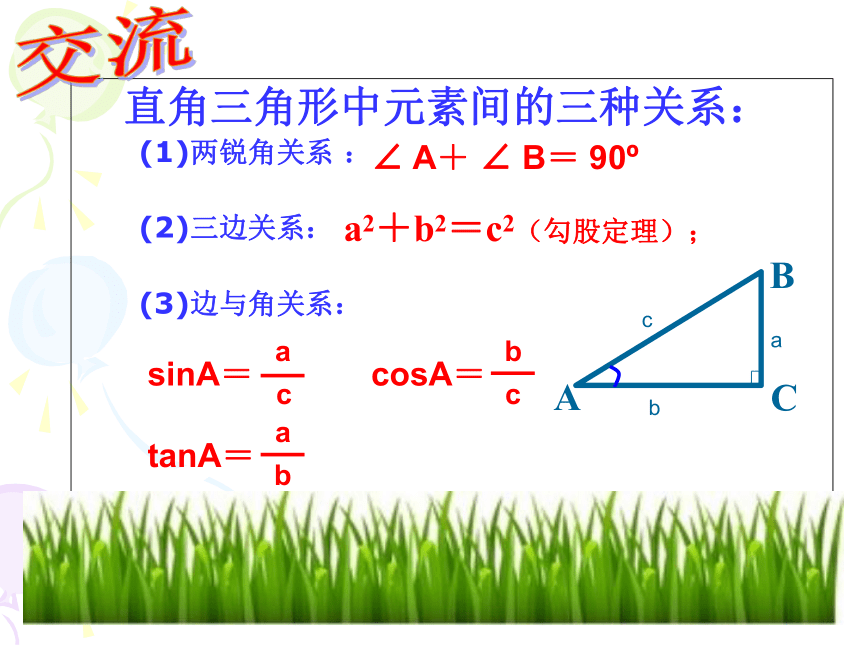
直角三角形中元素间的三种关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
交流
A
B
C
c
b
a
a2+b2=c2(勾股定理);
a
c
∠ A+ ∠ B= 90?
sinA=
b
c
cosA=
tanA=
a
b
1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B
(2)已知b=10,∠B=60°,求 ∠A ,a,c.
(3)已知c=20,∠A=60°,求 ∠B, a,b.
(4)已知a=1,b= ,求c, ∠A, ∠B
做一做
定义:
由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.
问题:1、解直角三角形需要什么条件?
思考
2、解直角三角形的条件可分为哪几类?
2、解直角三角形的条件可分为两大类:
①、已知一锐角、一边
(一锐角、一直角边或一斜边)
②、已知两边
(一直角边,一斜边或者两条直角边)
归纳:
1、解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)
小试牛刀
在Rt△ABC中,∠C=90°, ∠A=34°,AC=6解这个直角三角形。(结果精确到0.01,参考数据sin34°≈0.559 cos34° ≈ 0.829 tan34° ≈ 0.675)
A
B
C
1、如图,在⊿ABC中,∠A=30°,
tanB= ,AC=2 ,求AB.
A
C
B
D
应用(1)
(2011青岛中考)已知AB是⊙o的弦,半径等于6cm, ∠ACB=120°,求AB的长
应用(2)
如图, ⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长(精确到0.1)
参考数据:(sin36°≈0.588; cos36° ≈0.809; tan36° ≈0.727)
D
E
A
B
C
O.
H
应用(3)
36°
72°
多思多想
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
方法1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
方法2
B
D
E
A
C
2
1
60°
F
方法3
如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向。如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由(参考数值:√3≈1.73)
探索
60°
60°
60°
60°
60°
8海里
P
B
C
A
45°
60°
谢谢指导!!
复习旧知
1 什么是锐角三角函数?
2 我们计算锐角三角函数时都是在 什么条件下求值?
3 正切,正弦,余弦三角函数的边和角之间都有什么关系?
4
三角函数值
30°
45°
60°
sin
cos
tan
解直角三角形
学习目标:
1、理解解直角三角形的概念
2、会根据三角形中的已知量正确地求未知量
3、体会数学中的“化归” 思想
(1)在直角三角形中,除直角外共有几个 元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个
元素间有哪些等量关系呢?
A
B
C
a
c
b
a
想一想
直角三角形中元素间的三种关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
交流
A
B
C
c
b
a
a2+b2=c2(勾股定理);
a
c
∠ A+ ∠ B= 90?
sinA=
b
c
cosA=
tanA=
a
b
1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B
(2)已知b=10,∠B=60°,求 ∠A ,a,c.
(3)已知c=20,∠A=60°,求 ∠B, a,b.
(4)已知a=1,b= ,求c, ∠A, ∠B
做一做
定义:
由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.
问题:1、解直角三角形需要什么条件?
思考
2、解直角三角形的条件可分为哪几类?
2、解直角三角形的条件可分为两大类:
①、已知一锐角、一边
(一锐角、一直角边或一斜边)
②、已知两边
(一直角边,一斜边或者两条直角边)
归纳:
1、解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)
小试牛刀
在Rt△ABC中,∠C=90°, ∠A=34°,AC=6解这个直角三角形。(结果精确到0.01,参考数据sin34°≈0.559 cos34° ≈ 0.829 tan34° ≈ 0.675)
A
B
C
1、如图,在⊿ABC中,∠A=30°,
tanB= ,AC=2 ,求AB.
A
C
B
D
应用(1)
(2011青岛中考)已知AB是⊙o的弦,半径等于6cm, ∠ACB=120°,求AB的长
应用(2)
如图, ⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长(精确到0.1)
参考数据:(sin36°≈0.588; cos36° ≈0.809; tan36° ≈0.727)
D
E
A
B
C
O.
H
应用(3)
36°
72°
多思多想
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
方法1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
方法2
B
D
E
A
C
2
1
60°
F
方法3
如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向。如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由(参考数值:√3≈1.73)
探索
60°
60°
60°
60°
60°
8海里
P
B
C
A
45°
60°
谢谢指导!!
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
