冀教版初中数学九年级上册 26.3 解直角三角形 课件(21张ppt)
文档属性
| 名称 | 冀教版初中数学九年级上册 26.3 解直角三角形 课件(21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览


文档简介
解直角三角形
根据以上条件,你能求出塔身中心线与垂直中心线的夹角吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.
A
B
C
探讨比萨斜塔倾斜角的问题.
5.2
54.5
知 识回 顾
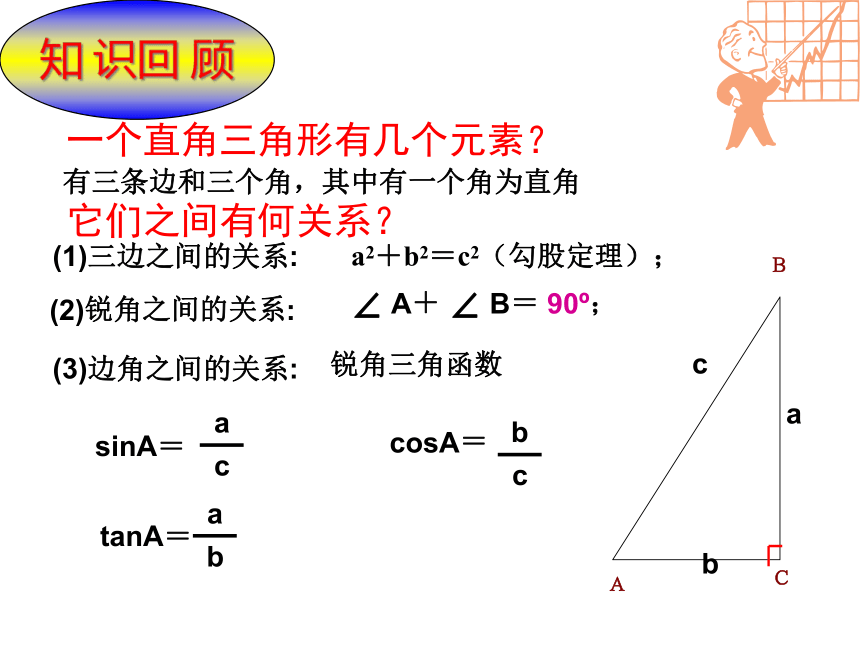
一个直角三角形有几个元素?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
有三条边和三个角,其中有一个角为直角
b
c
a
b
锐角三角函数
它们之间有何关系?
复习
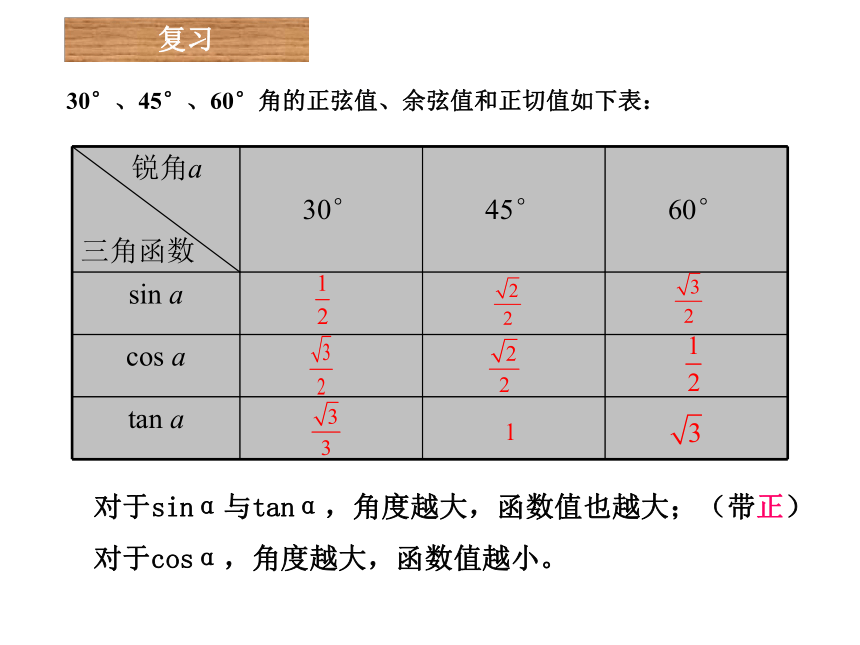
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小。
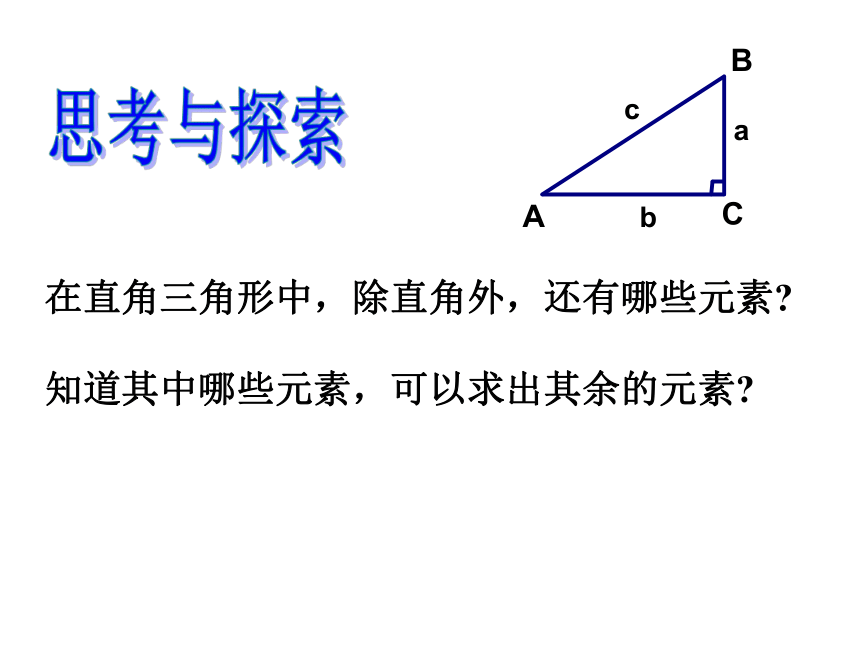
在直角三角形中,除直角外,还有哪些元素?
知道其中哪些元素,可以求出其余的元素?
思考与探索
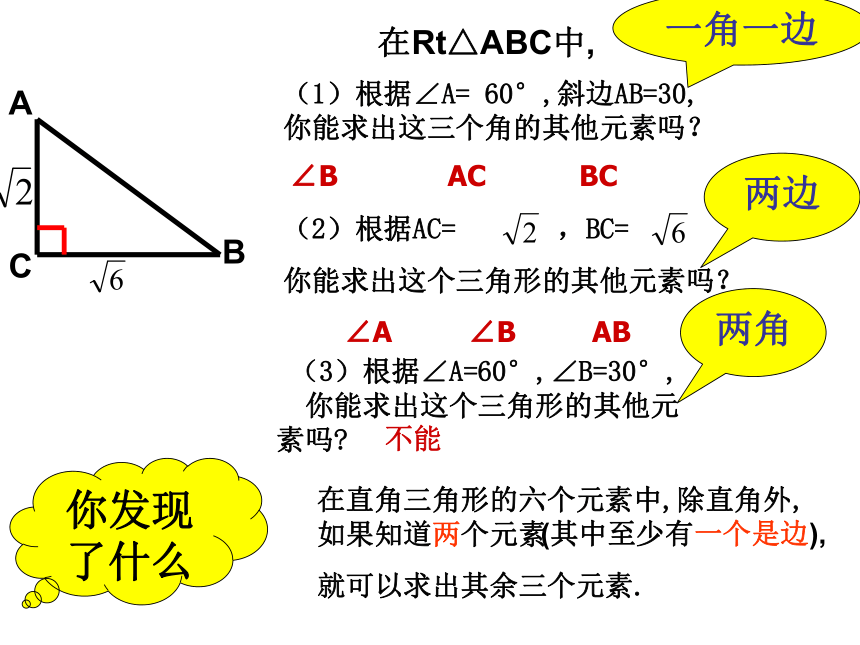
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
你能求出这三个角的其他元素吗?
A
在直角三角形的六个元素中,除直角外,如果知道两个元素
就可以求出其余三个元素.
(其中至少有一个是边),
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
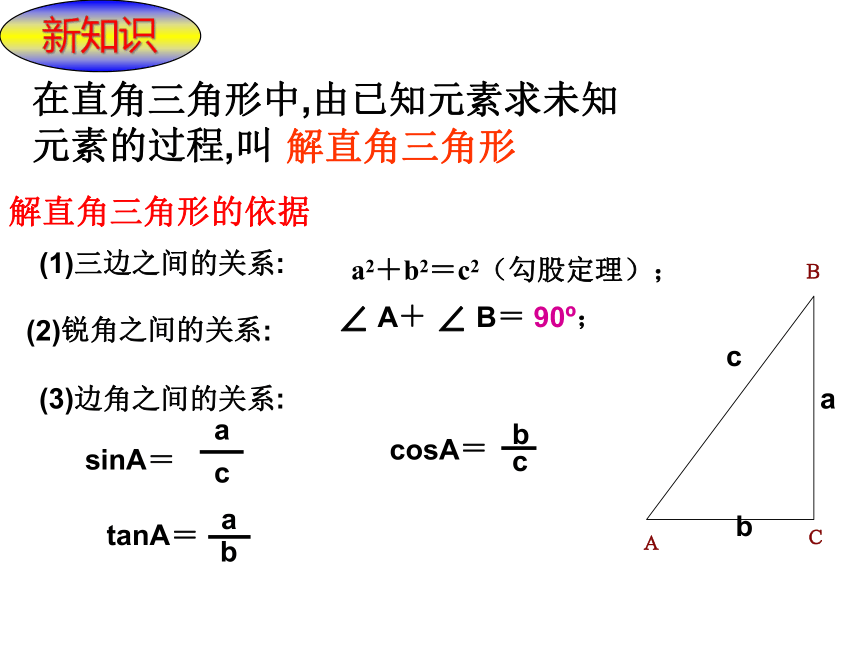
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据
A
C
B
a
b
c
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
新知识
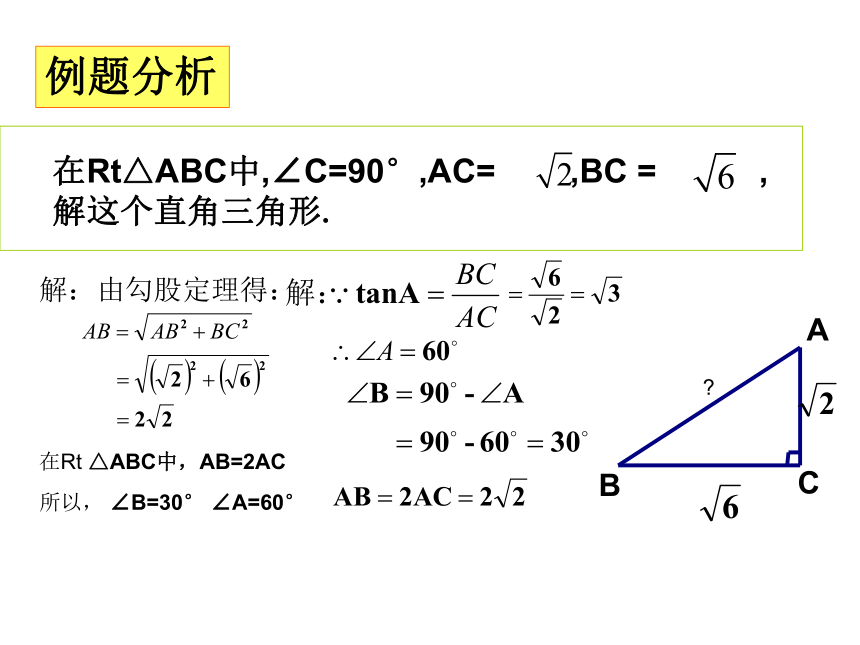
例题分析
在Rt△ABC中,∠C=90°,AC= ,BC = ,解这个直角三角形.
解:由勾股定理得:
在Rt △ABC中,AB=2AC
所以, ∠B=30° ∠A=60°
C
A
B
?
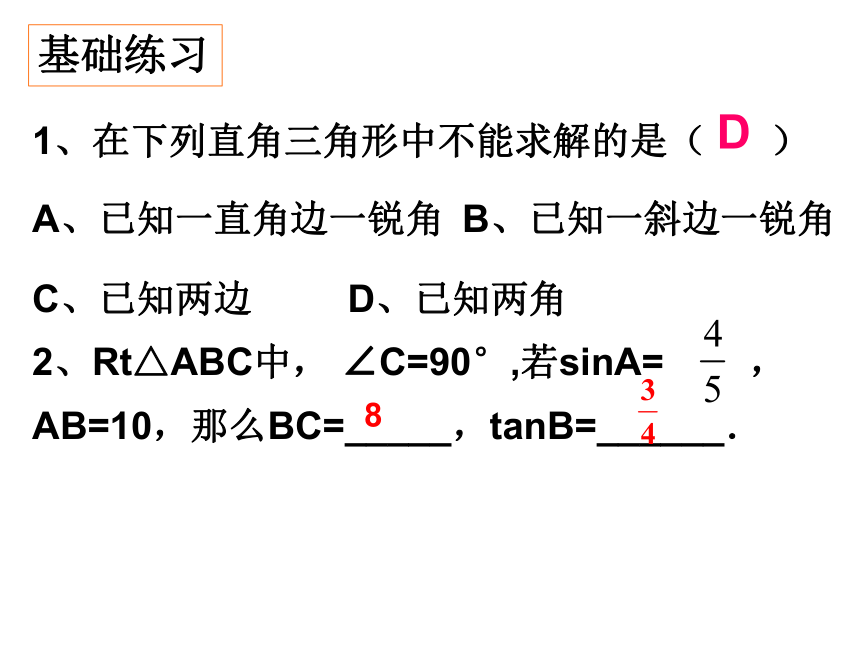
基础练习
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
2、Rt△ABC中, ∠C=90°,若sinA= ,AB=10,那么BC=_____,tanB=______.
D
8
基础练习
3.在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.
(1)c=8,∠A =60°;
(4)a=1, ∠B=30°.
(2) b= , c=4;
(3)a= , b=6 ;
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
4.已知a,c.则通过 ,求 ∠A
已知∠A,a. 则b= ,c= ;
3.已知∠A,b. 则a= , c= .
2. 已知∠A,c. 则a= ,b= ;
提高练习
5.已知a,b.则通过 ,求 ∠A
如图,在⊿ABC中,∠A=30°,
tanB= ,AC=2 ,求AB.
A
C
B
D
应用
中考点击
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
方法1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
方法2
A
B
C
D
E
2
1
60°
F
方法3
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
提示
D
B
A
C
D
试一试
A
B
C
D
E
变式
A
B
C
D
E
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
已知一边一角如何解直角三角形?
根据以上条件,你能求出塔身中心线与垂直中心线的夹角吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.
A
B
C
探讨比萨斜塔倾斜角的问题.
5.2
54.5
知 识回 顾
一个直角三角形有几个元素?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
有三条边和三个角,其中有一个角为直角
b
c
a
b
锐角三角函数
它们之间有何关系?
复习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小。
在直角三角形中,除直角外,还有哪些元素?
知道其中哪些元素,可以求出其余的元素?
思考与探索
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
你能求出这三个角的其他元素吗?
A
在直角三角形的六个元素中,除直角外,如果知道两个元素
就可以求出其余三个元素.
(其中至少有一个是边),
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据
A
C
B
a
b
c
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
新知识
例题分析
在Rt△ABC中,∠C=90°,AC= ,BC = ,解这个直角三角形.
解:由勾股定理得:
在Rt △ABC中,AB=2AC
所以, ∠B=30° ∠A=60°
C
A
B
?
基础练习
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
2、Rt△ABC中, ∠C=90°,若sinA= ,AB=10,那么BC=_____,tanB=______.
D
8
基础练习
3.在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.
(1)c=8,∠A =60°;
(4)a=1, ∠B=30°.
(2) b= , c=4;
(3)a= , b=6 ;
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
4.已知a,c.则通过 ,求 ∠A
已知∠A,a. 则b= ,c= ;
3.已知∠A,b. 则a= , c= .
2. 已知∠A,c. 则a= ,b= ;
提高练习
5.已知a,b.则通过 ,求 ∠A
如图,在⊿ABC中,∠A=30°,
tanB= ,AC=2 ,求AB.
A
C
B
D
应用
中考点击
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
方法1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
方法2
A
B
C
D
E
2
1
60°
F
方法3
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
提示
D
B
A
C
D
试一试
A
B
C
D
E
变式
A
B
C
D
E
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
已知一边一角如何解直角三角形?
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
