冀教版数学九年级下册第31章随机事件的概率复习课件(24张)
文档属性
| 名称 | 冀教版数学九年级下册第31章随机事件的概率复习课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 976.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:23:34 | ||
图片预览






文档简介
冀教版九下
第三十一章
随机事件的概率复习
事件的分类
确定事件
必然事件:在一定条件下,必然发生的事件,概率为________
不可能事件:在一定条件下,不可能发生的事件,概率为________
随机事件:在一定条件下,可能发生也可能不发生的事件,概率在0~1之间
概率的计算
1. 直接公式法:如果一个试验有n种等可能的结果,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=_________
2. 列表法:如果一次试验涉及两个因素,并且只有有限个等可能的结果,结果数目较多时,应列出所有可能的结果,通常采用列表法求事件发生的概率
1
0
一、知识点复习
概率的计算
3. 画树状图法:当一次试验涉及三个或更多的因素时,通常采用画树状图法来求事件发生的概率
4. 频率估计概率:一般地,做n次重复试验,如果事件A发生了m次,比值
稳定于某个常数P,那么事件A发生的概率:P(A)=P(0≤P(A)≤1)
5. 几何概型的概率公式:P(A)=
练习1 一个布袋内装有2个红球和3个黄球,这些球除颜色外其余都相同.
问题1:从中随机摸出一个球是白球是________事件,是黄球是_____事件,从中随机摸三个球,至少有一个球是黄球是_____事件(填“不可能”“必然”或“随机”);
问题2:随机摸出一个球,求摸到黄球的概率;
不可能
随机
必然
问题2 P(摸到黄球)= =
二、重难点突破
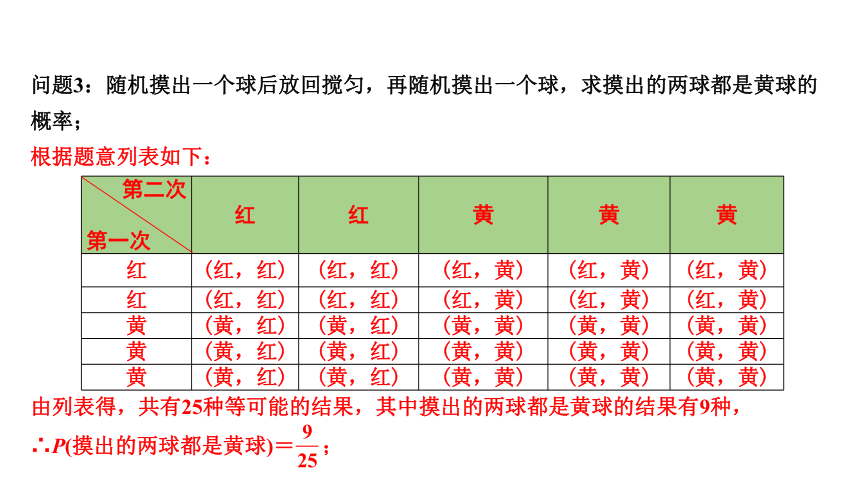
问题3:随机摸出一个球后放回搅匀,再随机摸出一个球,求摸出的两球都是黄球的概率;
{5940675A-B579-460E-94D1-54222C63F5DA}第二次
第一次
红
红
黄
黄
黄
红
(红,红)
(红,红)
(红,黄)
(红,黄)
(红,黄)
红
(红,红)
(红,红)
(红,黄)
(红,黄)
(红,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
(黄,黄)
由列表得,共有25种等可能的结果,其中摸出的两球都是黄球的结果有9种,
∴P(摸出的两球都是黄球)= ;
根据题意列表如下:
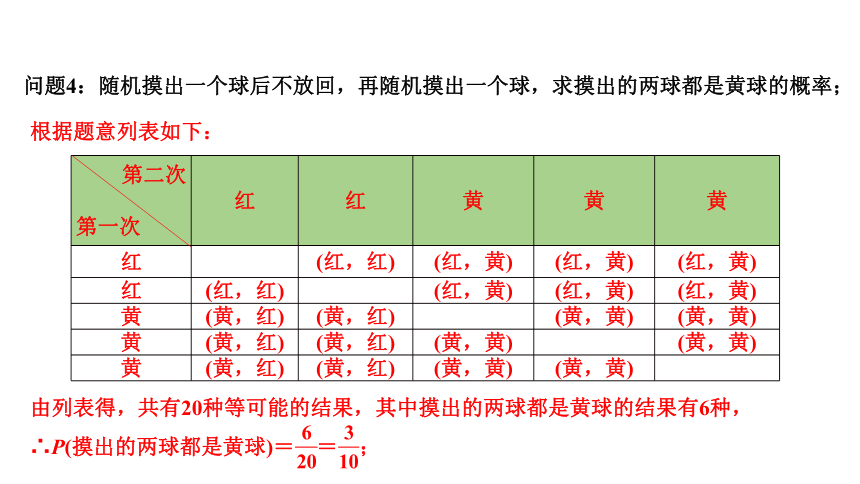
问题4:随机摸出一个球后不放回,再随机摸出一个球,求摸出的两球都是黄球的概率;
{5940675A-B579-460E-94D1-54222C63F5DA}第二次
第一次
红
红
黄
黄
黄
红
(红,红)
(红,黄)
(红,黄)
(红,黄)
红
(红,红)
(红,黄)
(红,黄)
(红,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
由列表得,共有20种等可能的结果,其中摸出的两球都是黄球的结果有6种,
∴P(摸出的两球都是黄球)= = ;
根据题意列表如下:
问题5:同时从袋中摸出两个球,求摸出的两球都是黄球的概率;
问题5 同时摸出两球,等同于不放回,故概率与问题4概率相同,
∴P(摸出的两球都是黄球)= ;
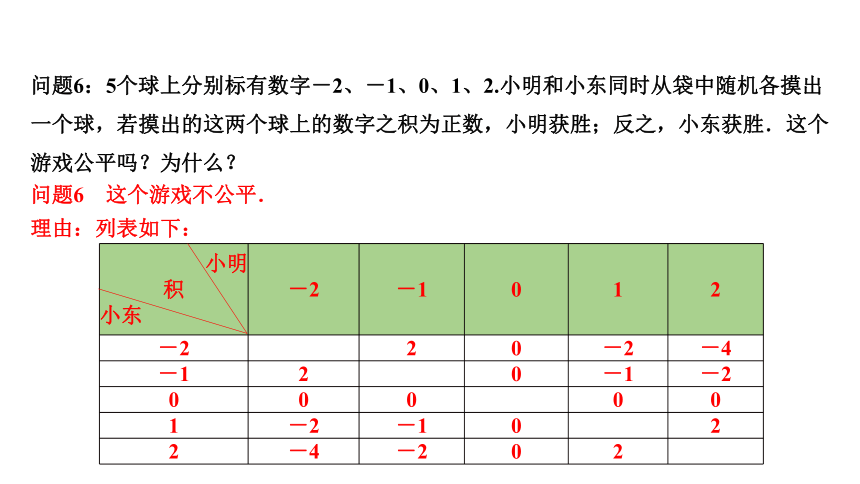
问题6:5个球上分别标有数字-2、-1、0、1、2.小明和小东同时从袋中随机各摸出一个球,若摸出的这两个球上的数字之积为正数,小明获胜;反之,小东获胜.这个游戏公平吗?为什么?
问题6 这个游戏不公平.
理由:列表如下:
{5940675A-B579-460E-94D1-54222C63F5DA}小明
积
小东
-2
-1
0
1
2
-2
2
0
-2
-4
-1
2
0
-1
-2
0
0
0
0
0
1
-2
-1
0
2
2
-4
-2
0
2
由列表得,共有20种等可能的结果,其中数字之积为正数的结果有4种,
∴P(小明获胜)= = ,
∴P(小东获胜)=1- = ,
∵ ≠ ,
∴这个游戏不公平.
练习2 现有五张背面完全相同的不透明卡片,其正面分别写有数字-3,-2,1,2,3,把这五张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为正数的概率;
(2)先随机抽取一张卡片,其上的数字作为点Q的横坐标,再从剩下的卡片中随机抽取一张,其上的数字作为点Q的纵坐标,试用画树状图或列表的方法求出点Q在第二象限内的概率.
解:(1)∵共有5种等可能情况.随机抽取一张卡片,抽取的卡片上的数字为正数有3种情况,
∴P(数字为正数)= ;
(2)画树状图如解图:
共有20种等可能的结果,其中点Q在第二象限的结果有6种,
∴P(点Q在第二象限)= = .
练习2题解图
1. (2017河北21题9分)编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记 0分.如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
第7题图
三、中考题演练
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
解:(1)第6号学生的积分为5×40%×1=2(分).(2分)
增补的条形统计图如解图:
第7题解图
(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;
(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
(2)∵这6名学生中,有4名学生的命中率高于50%,
∴P(选上命中率高于50%的学生)= = ;(6分)
(3)∵前6名学生的积分中3出现的次数最多,
∴前6名学生积分的众数是3分,(7分)
∴7名学生积分的众数是3分,
∴第7号学生命中了3次或没有命中,
∴第7号学生的积分是3分或0分.(9分)
2. (2018河北21题9分)老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图①)和不完整的扇形图(图②),其中条形图被墨迹遮盖了一部分.
第6题图
(1)求条形图中被遮盖的数,并写出册数的中位数;
解:(1)∵由条形统计图可知,读书6册的有6人,由扇形统计图可知,读书6册的占调查人数的25%,
∴调查人数为6÷25%=24(人),(1分)
∴读书5册的人数为24-5-6-4=9(人),
即被遮盖的数为9;(2分)
∵调查人数为24人,∴读书册数的中位数为第12人和第13人读书册数的平均数,
∵第12人和第13人的读书册数均为5册,
∴册数的中位数是5册;(3分)
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了________人.
3
(2)∵读书超过5册的共有6+4=10(人),
∴P(选中读书超过5册的学生)= = ;(6分)
【解法提示】∵读书4册与读书5册的人数共5+9=14(人),且中位数是5册,∴当中位数是第14个学生的读书册数时,中位数不发生变化,此时最多调查人数为2×(14-1)+1=27(人),∵27-24=3,∴最多补查了3人.
3. (2019河北22题9分)某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知P(一次拿到8元球)= .
(1)求这4个球价格的众数;
解:(1)∵P(一次拿到8元球)= ,
∴8元球为2个.
∴四个乒乓球的价格为7、8、8、9.
∴这四个球价格的众数为8;(3分)
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
(2)①相同;(4分)
理由:原四个球的中位数为8,拿走一个7元球后,剩余球的价格为8、8、9,中位数为8,与原来4个球价格的中位数相同.(7分)
{5940675A-B579-460E-94D1-54222C63F5DA} 又拿
先拿
第8题图
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
②列表如下:
{5940675A-B579-460E-94D1-54222C63F5DA} 又拿
先拿
8
8
9
8
(8,8)
(8,8)
(8,9)
8
(8,8)
(8,8)
(8,9)
9
(9,8)
(9,8)
(9,9)
由上表可知,共有9种等可能的结果,其中乙组两次都拿到8元球的结果共4种,(8分)
∴P(乙组两次都拿到8元球)= .(9分)
4. (2020河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
第9题图
(1)依题意,得移动一次共有4种等可能的情况,只有甲对乙错时,甲才能停留在正半轴上,∴P(甲的位置停留在正半轴上)= ;
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;
(2)依题意,得m=5+(-4)n+2(10-n)=25-6n.
当表示乙的点离原点O最近时,|m|取最小值,此时n=4,
∴表示乙的点离原点最近时n的值为4;
(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.
(3)k的值为3或5.
【解法提示】设两人间的距离为s,若甲、乙两人都对或都错,两人间的距离s=8-2k(k≤4)或s=2k-8(k>4),当s=2时,k=3或k=5;若甲、乙两人所猜结果一对一错,当甲对、乙错时两人间的距离为s=(5+2k)-(-3+4k)=8-2k (k≤4)或s=(-3+4k)-(5+2k)=2k-8(k>4),当s=2时,k=3或k=5;当乙对、甲错时两人间的距离为s=(5-4k)-(-3-2k)=8-2k(k≤4)或s=(-3-2k)-(5-4k)=2k-8(k>4),当s=2时,k=3或k=5;综上所述,k的值为3或5.
第三十一章
随机事件的概率复习
事件的分类
确定事件
必然事件:在一定条件下,必然发生的事件,概率为________
不可能事件:在一定条件下,不可能发生的事件,概率为________
随机事件:在一定条件下,可能发生也可能不发生的事件,概率在0~1之间
概率的计算
1. 直接公式法:如果一个试验有n种等可能的结果,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=_________
2. 列表法:如果一次试验涉及两个因素,并且只有有限个等可能的结果,结果数目较多时,应列出所有可能的结果,通常采用列表法求事件发生的概率
1
0
一、知识点复习
概率的计算
3. 画树状图法:当一次试验涉及三个或更多的因素时,通常采用画树状图法来求事件发生的概率
4. 频率估计概率:一般地,做n次重复试验,如果事件A发生了m次,比值
稳定于某个常数P,那么事件A发生的概率:P(A)=P(0≤P(A)≤1)
5. 几何概型的概率公式:P(A)=
练习1 一个布袋内装有2个红球和3个黄球,这些球除颜色外其余都相同.
问题1:从中随机摸出一个球是白球是________事件,是黄球是_____事件,从中随机摸三个球,至少有一个球是黄球是_____事件(填“不可能”“必然”或“随机”);
问题2:随机摸出一个球,求摸到黄球的概率;
不可能
随机
必然
问题2 P(摸到黄球)= =
二、重难点突破
问题3:随机摸出一个球后放回搅匀,再随机摸出一个球,求摸出的两球都是黄球的概率;
{5940675A-B579-460E-94D1-54222C63F5DA}第二次
第一次
红
红
黄
黄
黄
红
(红,红)
(红,红)
(红,黄)
(红,黄)
(红,黄)
红
(红,红)
(红,红)
(红,黄)
(红,黄)
(红,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
(黄,黄)
由列表得,共有25种等可能的结果,其中摸出的两球都是黄球的结果有9种,
∴P(摸出的两球都是黄球)= ;
根据题意列表如下:
问题4:随机摸出一个球后不放回,再随机摸出一个球,求摸出的两球都是黄球的概率;
{5940675A-B579-460E-94D1-54222C63F5DA}第二次
第一次
红
红
黄
黄
黄
红
(红,红)
(红,黄)
(红,黄)
(红,黄)
红
(红,红)
(红,黄)
(红,黄)
(红,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
黄
(黄,红)
(黄,红)
(黄,黄)
(黄,黄)
由列表得,共有20种等可能的结果,其中摸出的两球都是黄球的结果有6种,
∴P(摸出的两球都是黄球)= = ;
根据题意列表如下:
问题5:同时从袋中摸出两个球,求摸出的两球都是黄球的概率;
问题5 同时摸出两球,等同于不放回,故概率与问题4概率相同,
∴P(摸出的两球都是黄球)= ;
问题6:5个球上分别标有数字-2、-1、0、1、2.小明和小东同时从袋中随机各摸出一个球,若摸出的这两个球上的数字之积为正数,小明获胜;反之,小东获胜.这个游戏公平吗?为什么?
问题6 这个游戏不公平.
理由:列表如下:
{5940675A-B579-460E-94D1-54222C63F5DA}小明
积
小东
-2
-1
0
1
2
-2
2
0
-2
-4
-1
2
0
-1
-2
0
0
0
0
0
1
-2
-1
0
2
2
-4
-2
0
2
由列表得,共有20种等可能的结果,其中数字之积为正数的结果有4种,
∴P(小明获胜)= = ,
∴P(小东获胜)=1- = ,
∵ ≠ ,
∴这个游戏不公平.
练习2 现有五张背面完全相同的不透明卡片,其正面分别写有数字-3,-2,1,2,3,把这五张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为正数的概率;
(2)先随机抽取一张卡片,其上的数字作为点Q的横坐标,再从剩下的卡片中随机抽取一张,其上的数字作为点Q的纵坐标,试用画树状图或列表的方法求出点Q在第二象限内的概率.
解:(1)∵共有5种等可能情况.随机抽取一张卡片,抽取的卡片上的数字为正数有3种情况,
∴P(数字为正数)= ;
(2)画树状图如解图:
共有20种等可能的结果,其中点Q在第二象限的结果有6种,
∴P(点Q在第二象限)= = .
练习2题解图
1. (2017河北21题9分)编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记 0分.如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
第7题图
三、中考题演练
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
解:(1)第6号学生的积分为5×40%×1=2(分).(2分)
增补的条形统计图如解图:
第7题解图
(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;
(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
(2)∵这6名学生中,有4名学生的命中率高于50%,
∴P(选上命中率高于50%的学生)= = ;(6分)
(3)∵前6名学生的积分中3出现的次数最多,
∴前6名学生积分的众数是3分,(7分)
∴7名学生积分的众数是3分,
∴第7号学生命中了3次或没有命中,
∴第7号学生的积分是3分或0分.(9分)
2. (2018河北21题9分)老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图①)和不完整的扇形图(图②),其中条形图被墨迹遮盖了一部分.
第6题图
(1)求条形图中被遮盖的数,并写出册数的中位数;
解:(1)∵由条形统计图可知,读书6册的有6人,由扇形统计图可知,读书6册的占调查人数的25%,
∴调查人数为6÷25%=24(人),(1分)
∴读书5册的人数为24-5-6-4=9(人),
即被遮盖的数为9;(2分)
∵调查人数为24人,∴读书册数的中位数为第12人和第13人读书册数的平均数,
∵第12人和第13人的读书册数均为5册,
∴册数的中位数是5册;(3分)
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了________人.
3
(2)∵读书超过5册的共有6+4=10(人),
∴P(选中读书超过5册的学生)= = ;(6分)
【解法提示】∵读书4册与读书5册的人数共5+9=14(人),且中位数是5册,∴当中位数是第14个学生的读书册数时,中位数不发生变化,此时最多调查人数为2×(14-1)+1=27(人),∵27-24=3,∴最多补查了3人.
3. (2019河北22题9分)某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知P(一次拿到8元球)= .
(1)求这4个球价格的众数;
解:(1)∵P(一次拿到8元球)= ,
∴8元球为2个.
∴四个乒乓球的价格为7、8、8、9.
∴这四个球价格的众数为8;(3分)
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
(2)①相同;(4分)
理由:原四个球的中位数为8,拿走一个7元球后,剩余球的价格为8、8、9,中位数为8,与原来4个球价格的中位数相同.(7分)
{5940675A-B579-460E-94D1-54222C63F5DA} 又拿
先拿
第8题图
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
②列表如下:
{5940675A-B579-460E-94D1-54222C63F5DA} 又拿
先拿
8
8
9
8
(8,8)
(8,8)
(8,9)
8
(8,8)
(8,8)
(8,9)
9
(9,8)
(9,8)
(9,9)
由上表可知,共有9种等可能的结果,其中乙组两次都拿到8元球的结果共4种,(8分)
∴P(乙组两次都拿到8元球)= .(9分)
4. (2020河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
第9题图
(1)依题意,得移动一次共有4种等可能的情况,只有甲对乙错时,甲才能停留在正半轴上,∴P(甲的位置停留在正半轴上)= ;
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;
(2)依题意,得m=5+(-4)n+2(10-n)=25-6n.
当表示乙的点离原点O最近时,|m|取最小值,此时n=4,
∴表示乙的点离原点最近时n的值为4;
(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.
(3)k的值为3或5.
【解法提示】设两人间的距离为s,若甲、乙两人都对或都错,两人间的距离s=8-2k(k≤4)或s=2k-8(k>4),当s=2时,k=3或k=5;若甲、乙两人所猜结果一对一错,当甲对、乙错时两人间的距离为s=(5+2k)-(-3+4k)=8-2k (k≤4)或s=(-3+4k)-(5+2k)=2k-8(k>4),当s=2时,k=3或k=5;当乙对、甲错时两人间的距离为s=(5-4k)-(-3-2k)=8-2k(k≤4)或s=(-3-2k)-(5-4k)=2k-8(k>4),当s=2时,k=3或k=5;综上所述,k的值为3或5.
