京改版八年级上册数学12.6等腰三角形(1)课件(36张ppt)
文档属性
| 名称 | 京改版八年级上册数学12.6等腰三角形(1)课件(36张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 11:42:43 | ||
图片预览








文档简介
等腰三角形(1)
初二年级 数学
故宫太和殿
白塔寺藻井天花
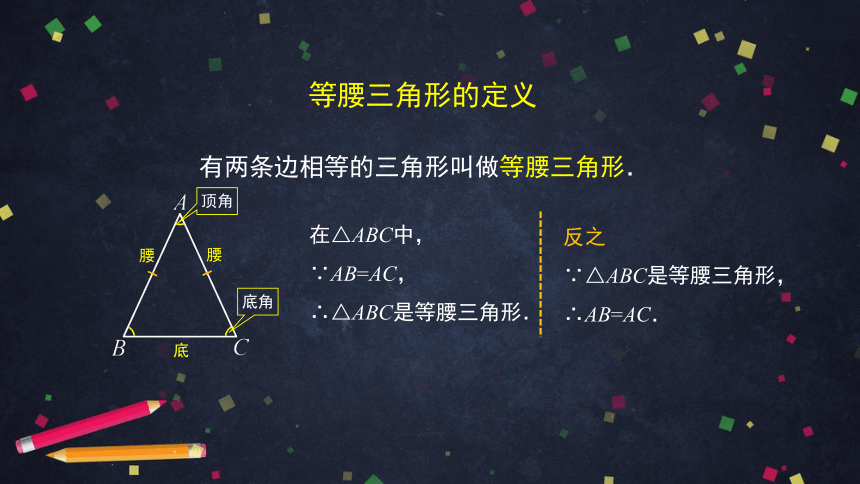
等腰三角形的定义
有两条边相等的三角形叫做等腰三角形.
在△ABC中,
∵AB=AC,
∴△ABC是等腰三角形.
反之
∵△ABC是等腰三角形,
∴AB=AC.
腰
腰
底
顶角
底角
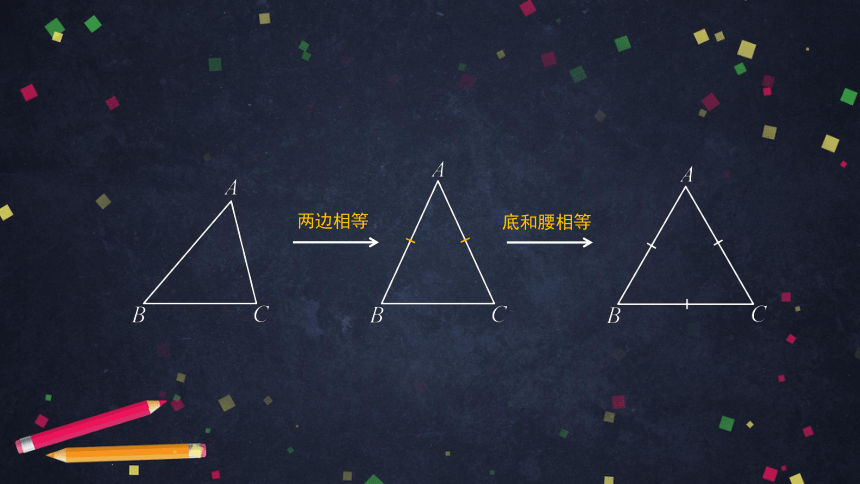
两边相等
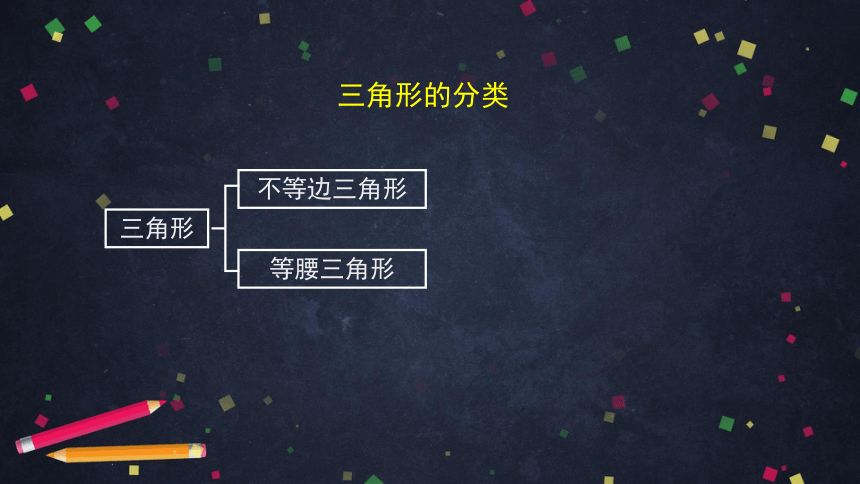
三角形的分类
三角形
不等边三角形
等腰三角形
两边相等
底和腰相等
三角形的分类
三角形
不等边三角形
等腰三角形
底边和腰不等的等腰三角形
等边三角形
三角形的分类
等边三角形
等腰三角形
不等边三角形
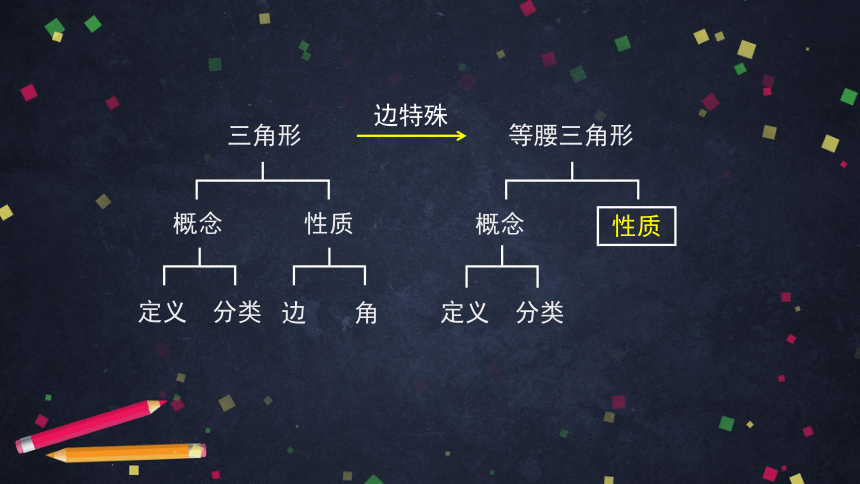
概念
性质
三角形
等腰三角形
定义
分类
边
角
概念
定义
分类
性质
边特殊
测量
折叠
猜想 等腰三角形的两个底角相等.
猜想 等腰三角形的两个底角相等.
题设
结论
已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C.
分析:
作∠BAC的平分线
∠B=∠C
∠BAD=∠CAD
△ABD≌△ACD
AB=AC,
,AD=AD
证明:
作∠BAC的平分线交BC于D,
∵AD平分∠BAC,
∴∠BAD=∠CAD.
证明:
在△ABD和△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS).
∴∠B=∠C.
分析:
作BC边上的中线
∠B=∠C
BD=CD
△ABD≌△ACD
AB=AC
AD=AD
分析:
作BC边上的高
∠B=∠C
∠ADB=∠ADC=90°
△ABD≌△ACD
AB=AC,
,AD=AD
×
性质定理1 等腰三角形的两个底角相等(简记为:等边对等角).
在△ABC中,
∵AB=AC,
∴∠B=∠C.
文字语言
符号语言
图形语言
性质定理2
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合
(简记为:三线合一).
1.如果等腰三角形中的一条线段是顶角平分线,那么它也是底边上的中线和底边上的高.
符号语言
在△ABC中,
∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC.
图形语言
2.如果等腰三角形中的一条线段是这个底边上的中线,那么它也是顶角的平分线和底边上的高.
符号语言
在△ABC中,
∵AB=AC,BD=CD,
∴AD平分∠BAC,AD⊥BC.
图形语言
3.如果等腰三角形中一条线段是这个底边上的高,那么它也是顶角的平分线和底边上的中线.
符号语言
在△ABC中,
∵AB=AC,AD⊥BC,
∴AD平分∠BAC,BD=CD.
图形语言
概念
性质
三角形
等腰三角形
定义
分类
边
角
概念
定义
分类
性质
边
角
主要线段
概念
性质
等腰三角形
等边三角形
定义
分类
概念
性质
边
角
主要线段
∵△ABC是等边三角形,
∴AB=AC=BC.
有三条边相等的三角形叫做等边三角形.
思考探究
AB=AC
分析:
∠A=∠B=∠C
∠B=∠C
∠A+∠B+∠C=180°
AC=BC
∠A=∠B
∠A=∠B=∠C=60°
性质定理 等边三角形的每个角都相等,并且都等于60°.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°.
文字语言
符号语言
图形语言
思考探究
课堂小结
三角形
不等边三角形
等腰三角形
底边和腰不等的等腰三角形
等边三角形
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}性质
边
角
主要线段
等腰三角形
等边三角形
作业
1.复习本节课内容.
2.填空:如图,在△ABC中,AB=AC,∠A=120°.
(1)则∠B= , ∠C= .
(2)过点A作AD⊥BC于D,则∠BAD= .
如果BC=10,那么BD= .
同学们,再见!
初二年级 数学
故宫太和殿
白塔寺藻井天花
等腰三角形的定义
有两条边相等的三角形叫做等腰三角形.
在△ABC中,
∵AB=AC,
∴△ABC是等腰三角形.
反之
∵△ABC是等腰三角形,
∴AB=AC.
腰
腰
底
顶角
底角
两边相等
三角形的分类
三角形
不等边三角形
等腰三角形
两边相等
底和腰相等
三角形的分类
三角形
不等边三角形
等腰三角形
底边和腰不等的等腰三角形
等边三角形
三角形的分类
等边三角形
等腰三角形
不等边三角形
概念
性质
三角形
等腰三角形
定义
分类
边
角
概念
定义
分类
性质
边特殊
测量
折叠
猜想 等腰三角形的两个底角相等.
猜想 等腰三角形的两个底角相等.
题设
结论
已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C.
分析:
作∠BAC的平分线
∠B=∠C
∠BAD=∠CAD
△ABD≌△ACD
AB=AC,
,AD=AD
证明:
作∠BAC的平分线交BC于D,
∵AD平分∠BAC,
∴∠BAD=∠CAD.
证明:
在△ABD和△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS).
∴∠B=∠C.
分析:
作BC边上的中线
∠B=∠C
BD=CD
△ABD≌△ACD
AB=AC
AD=AD
分析:
作BC边上的高
∠B=∠C
∠ADB=∠ADC=90°
△ABD≌△ACD
AB=AC,
,AD=AD
×
性质定理1 等腰三角形的两个底角相等(简记为:等边对等角).
在△ABC中,
∵AB=AC,
∴∠B=∠C.
文字语言
符号语言
图形语言
性质定理2
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合
(简记为:三线合一).
1.如果等腰三角形中的一条线段是顶角平分线,那么它也是底边上的中线和底边上的高.
符号语言
在△ABC中,
∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC.
图形语言
2.如果等腰三角形中的一条线段是这个底边上的中线,那么它也是顶角的平分线和底边上的高.
符号语言
在△ABC中,
∵AB=AC,BD=CD,
∴AD平分∠BAC,AD⊥BC.
图形语言
3.如果等腰三角形中一条线段是这个底边上的高,那么它也是顶角的平分线和底边上的中线.
符号语言
在△ABC中,
∵AB=AC,AD⊥BC,
∴AD平分∠BAC,BD=CD.
图形语言
概念
性质
三角形
等腰三角形
定义
分类
边
角
概念
定义
分类
性质
边
角
主要线段
概念
性质
等腰三角形
等边三角形
定义
分类
概念
性质
边
角
主要线段
∵△ABC是等边三角形,
∴AB=AC=BC.
有三条边相等的三角形叫做等边三角形.
思考探究
AB=AC
分析:
∠A=∠B=∠C
∠B=∠C
∠A+∠B+∠C=180°
AC=BC
∠A=∠B
∠A=∠B=∠C=60°
性质定理 等边三角形的每个角都相等,并且都等于60°.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°.
文字语言
符号语言
图形语言
思考探究
课堂小结
三角形
不等边三角形
等腰三角形
底边和腰不等的等腰三角形
等边三角形
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}性质
边
角
主要线段
等腰三角形
等边三角形
作业
1.复习本节课内容.
2.填空:如图,在△ABC中,AB=AC,∠A=120°.
(1)则∠B= , ∠C= .
(2)过点A作AD⊥BC于D,则∠BAD= .
如果BC=10,那么BD= .
同学们,再见!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
