人教版八年级上册14.1.4整式的乘法(第三课时)课件(28张PPT)
文档属性
| 名称 | 人教版八年级上册14.1.4整式的乘法(第三课时)课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 383.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 12:01:17 | ||
图片预览




文档简介
整式的乘法(第三课时)
幂的运算性质是什么?
同底数幂的乘法:
幂的乘方:
积的乘方:
温故知新
单项式乘单项式的运算法则是什么?
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
温故知新
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘多项式的运算法则是什么?
温故知新
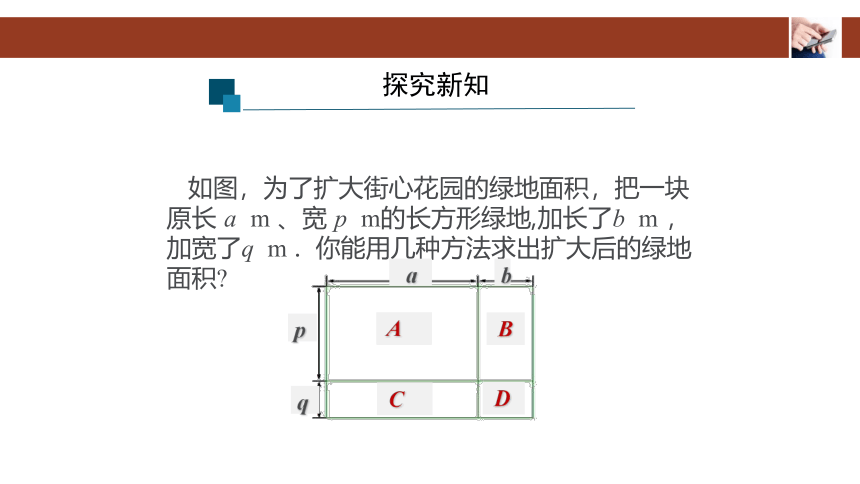
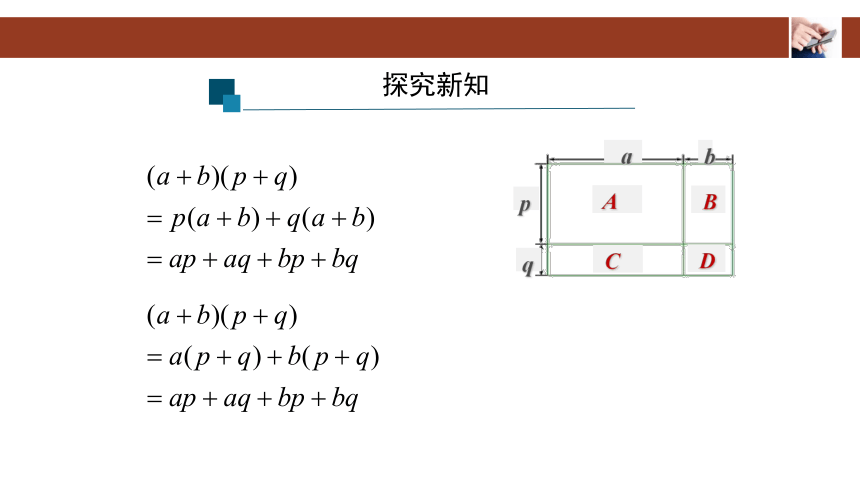
如图,为了扩大街心花园的绿地面积,把一块原长 a m 、宽 p m的长方形绿地,加长了b m ,加宽了q m . 你能用几种方法求出扩大后的绿地面积?
a
b
p
q
A
B
C
D
探究新知
a
b
p
q
A
B
C
D
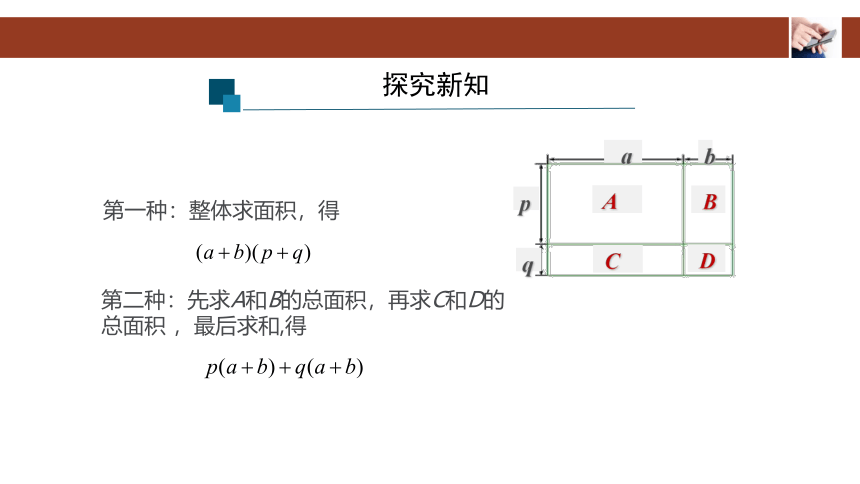
第一种:整体求面积,得
第二种:先求A和B的总面积,再求C和D的总面积 ,最后求和,得
探究新知
a
b
p
q
A
B
C
D
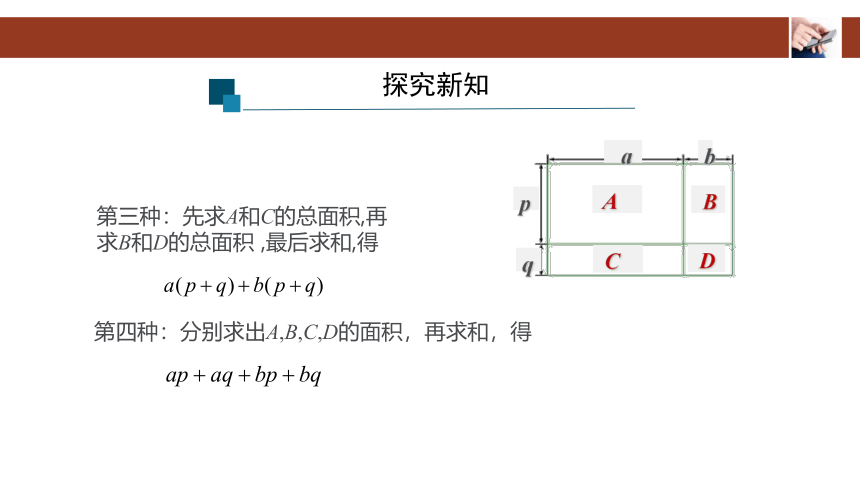
第三种:先求A和C的总面积,再
求B和D的总面积 ,最后求和,得
第四种:分别求出A,B,C,D的面积,再求和,得
探究新知
a
b
p
q
A
B
C
D
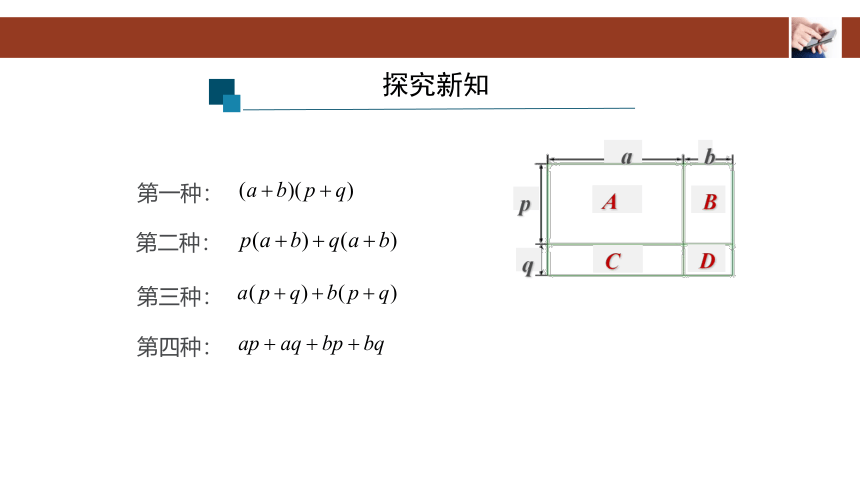
第三种:
第四种:
第一种:
第二种:
探究新知
a
b
p
q
A
B
C
D
探究新知
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘法则:
探究新知
例 计算
(2)
(3)
(1)
例题解析
例 计算
(1)
解:
例题解析
例 计算
(2)
解:
例题解析
例 计算
(3)
解:
多乘多
↓
单乘多
↓
单乘单
例题解析
练习 计算
(1)
解:
巩固练习
练习 计算
(2)
解:
巩固练习
例 如图,边长为 的正方形纸片,剪出
一个边长为 的正方形之后,剩余部分可剪
拼成一个长方形(不重叠无缝隙),若拼成的
长方形一边长为 3,根据剩余部分的面积,
写出一个正确的等式是________________.
例题解析
分析:剩余部分的面积有两种方法表示:
1、大正方形的面积减去小正方形的面积:
2、剩余的部分剪拼成一个小长方形的面积:
整理得:
所以,等式是:
数
形
结
合
A
A
B
B
例题解析
证明:
左边
右边
例题解析
例 已知 ,
求 的值.
消元思想
例题解析
例 如果 求 的值 .
整体思想
例题解析
解:整理一次项得:
例 如果 的乘积中不含 的一次项,
求 的值 .
例题解析
练习
巩固练习
1 数学知识
2 思想方法
整体思想
转化思想:
多乘多→单乘多→单乘单
多项式与多项式相乘,先用一个多项式的每一项
乘另一个多项式的每一项,再把所得的积相加.
数形结合
课堂小结
1. 计算:
课后作业
2.计算
3.已知 ,求 的值 .
课后作业
同学们,再见!
练习
巩固练习
幂的运算性质是什么?
同底数幂的乘法:
幂的乘方:
积的乘方:
温故知新
单项式乘单项式的运算法则是什么?
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
温故知新
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘多项式的运算法则是什么?
温故知新
如图,为了扩大街心花园的绿地面积,把一块原长 a m 、宽 p m的长方形绿地,加长了b m ,加宽了q m . 你能用几种方法求出扩大后的绿地面积?
a
b
p
q
A
B
C
D
探究新知
a
b
p
q
A
B
C
D
第一种:整体求面积,得
第二种:先求A和B的总面积,再求C和D的总面积 ,最后求和,得
探究新知
a
b
p
q
A
B
C
D
第三种:先求A和C的总面积,再
求B和D的总面积 ,最后求和,得
第四种:分别求出A,B,C,D的面积,再求和,得
探究新知
a
b
p
q
A
B
C
D
第三种:
第四种:
第一种:
第二种:
探究新知
a
b
p
q
A
B
C
D
探究新知
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘法则:
探究新知
例 计算
(2)
(3)
(1)
例题解析
例 计算
(1)
解:
例题解析
例 计算
(2)
解:
例题解析
例 计算
(3)
解:
多乘多
↓
单乘多
↓
单乘单
例题解析
练习 计算
(1)
解:
巩固练习
练习 计算
(2)
解:
巩固练习
例 如图,边长为 的正方形纸片,剪出
一个边长为 的正方形之后,剩余部分可剪
拼成一个长方形(不重叠无缝隙),若拼成的
长方形一边长为 3,根据剩余部分的面积,
写出一个正确的等式是________________.
例题解析
分析:剩余部分的面积有两种方法表示:
1、大正方形的面积减去小正方形的面积:
2、剩余的部分剪拼成一个小长方形的面积:
整理得:
所以,等式是:
数
形
结
合
A
A
B
B
例题解析
证明:
左边
右边
例题解析
例 已知 ,
求 的值.
消元思想
例题解析
例 如果 求 的值 .
整体思想
例题解析
解:整理一次项得:
例 如果 的乘积中不含 的一次项,
求 的值 .
例题解析
练习
巩固练习
1 数学知识
2 思想方法
整体思想
转化思想:
多乘多→单乘多→单乘单
多项式与多项式相乘,先用一个多项式的每一项
乘另一个多项式的每一项,再把所得的积相加.
数形结合
课堂小结
1. 计算:
课后作业
2.计算
3.已知 ,求 的值 .
课后作业
同学们,再见!
练习
巩固练习
