人教版八年级上册第十四章整式的乘法与因式分解全章复习(第二课时)课件(42张)
文档属性
| 名称 | 人教版八年级上册第十四章整式的乘法与因式分解全章复习(第二课时)课件(42张) |  | |
| 格式 | pptx | ||
| 文件大小 | 572.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 17:46:23 | ||
图片预览








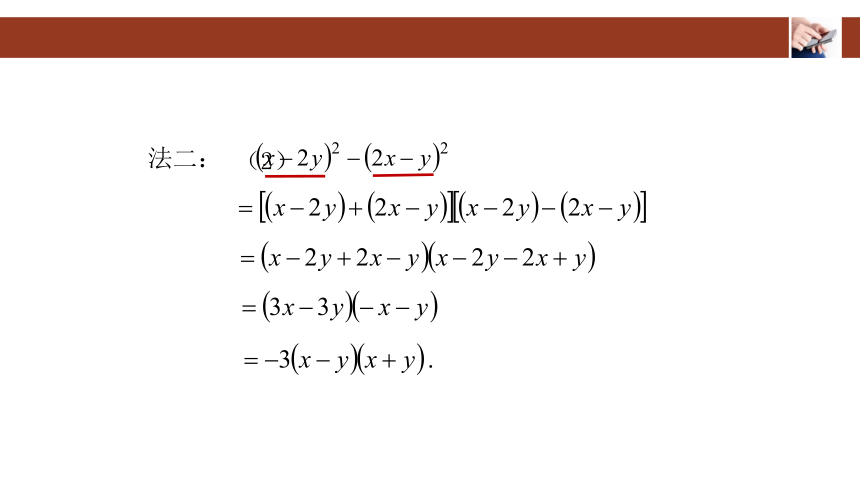


文档简介
整式的乘法与因式分解
全章复习(第二课时)
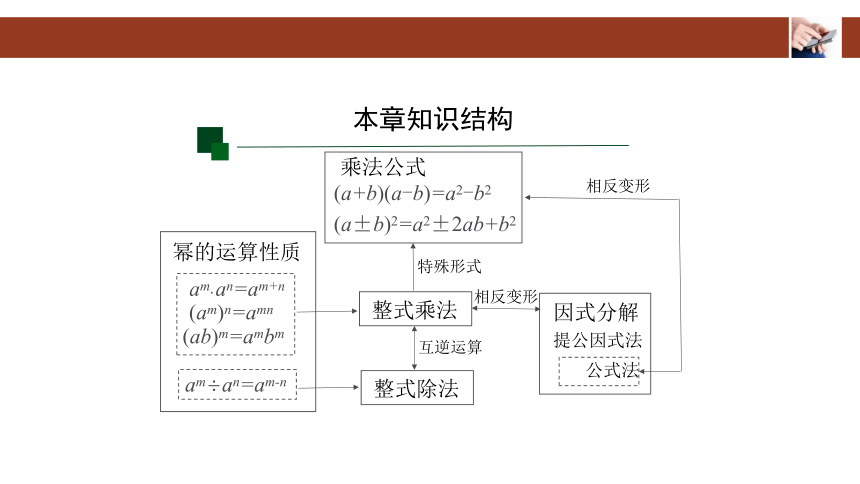
本章知识结构
整式乘法
幂的运算性质
am an=am+n
(am)n=amn
(ab)m=ambm
.
(a+b)(a-b)=a2-b2
(a±b)2=a2±2ab+b2
乘法公式
特殊形式
因式分解
提公因式法
公式法
相反变形
相反变形
互逆运算
整式除法
am÷an=am-n
复习回顾
1.因式分解的定义:
整式乘法
因式分解
相反变形
把几个整式相乘,得到一个新的整式.
把一个多项式化成几个整式的积的形式.
(1)先提公因式: ;
(2)观察项数:
(3)检查分解是否彻底.
复习回顾
2.因式分解的方法:
非负性
典例选讲
例 下列各式中,从左到右的变形属于因式分解的是( ).
A.
B.
C.
D.
C
因式分解:把一个多项式化成
几个整式的积的形式.
典例选讲
例 下列各式中,从左到右的变形属于因式分解的是( ).
A.
B.
C.
D.
C
因式分解:把一个多项式化成
几个整式的积的形式.
小结:判断变形是否属于因式分解,这个变形要符合因式分解定义的每一个条件.
例 分解因式:
(1) ;
(2) .
例 分解因式:
(1) ;
解:
小结:分解因式中,提公因式是我们的首选方法,检查因式分解是否彻底也是很关键的一步.
例 分解因式:
(2)
法一:
(2)
法二:
小结:通过观察代数式的特点,可以直接分解因式, 也可以先整理,然后再分解因式.
巩固练习 分解因式:
(1) ;
(2) .
巩固练习 分解因式:
(1)
(2)
积的乘方
例(1)已知 , ,
求 的值;
(2)若 ,
求 的值.
例(1)已知 , ,
求 的值;
分析:
公因式
完全平方公式
例(1)已知 , ,
求 的值;
解:
将 , 代入,
原式
分析:
(2)若 ,求 的值.
分析:
(2)若 ,求 的值.
完全平方公式
非负性
(2)若 ,求 的值.
解:
小结:通过观察题目中代数式的特征,从比较复杂的条件入手,利用分解因式进行计算,或者化简,从而解决问题.
知识拓展
整式乘法:
分解因式:
观察:
观察:
观察:
分解因式:
观察:
观察:
观察:
分解因式:
例 分解因式:
解:
1
1
例 分解因式:
解:
1
1
1
-8
2
-4
1
1
例 分解因式:
解:
1
1
1
-8
1
-8
+( )=-7
例 分解因式:
解:
1
1
2
-4
2
-4
+( )=-2
巩固练习 分解因式:
(1) ;
(2) .
巩固练习 分解因式:
(1)
解:
1
1
-1
3
-1
3
+ = 2
巩固练习 分解因式:
(1)
解:
1
1
-1
3
-1
3
+ = 2
巩固练习 分解因式:
(2)
解:
巩固练习 分解因式:
(2)
解:
1
1
-1
-6
-1
+(-6)=-7
1
1
-2
-3
-2
+(-3)=-5
小结:先观察符号,再进行尝试,不断积累经验,会比较迅速地找到正确的结果.
归纳总结
1.复习因式分解的定义与方法,并利用因式分解
解决有关问题;
2.了解 型式子因式分解的方法.
课后作业
1.分解因式:
(1) ; (2) ;
(3) ; (4) .
2.已知 , ,求 的值.
同学们,再见!
全章复习(第二课时)
本章知识结构
整式乘法
幂的运算性质
am an=am+n
(am)n=amn
(ab)m=ambm
.
(a+b)(a-b)=a2-b2
(a±b)2=a2±2ab+b2
乘法公式
特殊形式
因式分解
提公因式法
公式法
相反变形
相反变形
互逆运算
整式除法
am÷an=am-n
复习回顾
1.因式分解的定义:
整式乘法
因式分解
相反变形
把几个整式相乘,得到一个新的整式.
把一个多项式化成几个整式的积的形式.
(1)先提公因式: ;
(2)观察项数:
(3)检查分解是否彻底.
复习回顾
2.因式分解的方法:
非负性
典例选讲
例 下列各式中,从左到右的变形属于因式分解的是( ).
A.
B.
C.
D.
C
因式分解:把一个多项式化成
几个整式的积的形式.
典例选讲
例 下列各式中,从左到右的变形属于因式分解的是( ).
A.
B.
C.
D.
C
因式分解:把一个多项式化成
几个整式的积的形式.
小结:判断变形是否属于因式分解,这个变形要符合因式分解定义的每一个条件.
例 分解因式:
(1) ;
(2) .
例 分解因式:
(1) ;
解:
小结:分解因式中,提公因式是我们的首选方法,检查因式分解是否彻底也是很关键的一步.
例 分解因式:
(2)
法一:
(2)
法二:
小结:通过观察代数式的特点,可以直接分解因式, 也可以先整理,然后再分解因式.
巩固练习 分解因式:
(1) ;
(2) .
巩固练习 分解因式:
(1)
(2)
积的乘方
例(1)已知 , ,
求 的值;
(2)若 ,
求 的值.
例(1)已知 , ,
求 的值;
分析:
公因式
完全平方公式
例(1)已知 , ,
求 的值;
解:
将 , 代入,
原式
分析:
(2)若 ,求 的值.
分析:
(2)若 ,求 的值.
完全平方公式
非负性
(2)若 ,求 的值.
解:
小结:通过观察题目中代数式的特征,从比较复杂的条件入手,利用分解因式进行计算,或者化简,从而解决问题.
知识拓展
整式乘法:
分解因式:
观察:
观察:
观察:
分解因式:
观察:
观察:
观察:
分解因式:
例 分解因式:
解:
1
1
例 分解因式:
解:
1
1
1
-8
2
-4
1
1
例 分解因式:
解:
1
1
1
-8
1
-8
+( )=-7
例 分解因式:
解:
1
1
2
-4
2
-4
+( )=-2
巩固练习 分解因式:
(1) ;
(2) .
巩固练习 分解因式:
(1)
解:
1
1
-1
3
-1
3
+ = 2
巩固练习 分解因式:
(1)
解:
1
1
-1
3
-1
3
+ = 2
巩固练习 分解因式:
(2)
解:
巩固练习 分解因式:
(2)
解:
1
1
-1
-6
-1
+(-6)=-7
1
1
-2
-3
-2
+(-3)=-5
小结:先观察符号,再进行尝试,不断积累经验,会比较迅速地找到正确的结果.
归纳总结
1.复习因式分解的定义与方法,并利用因式分解
解决有关问题;
2.了解 型式子因式分解的方法.
课后作业
1.分解因式:
(1) ; (2) ;
(3) ; (4) .
2.已知 , ,求 的值.
同学们,再见!
