人教版八年级数学下册17章勾股定理复习与小结课件 (共31张PPT)
文档属性
| 名称 | 人教版八年级数学下册17章勾股定理复习与小结课件 (共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 797.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览










文档简介
17章勾股定理
复习与小结
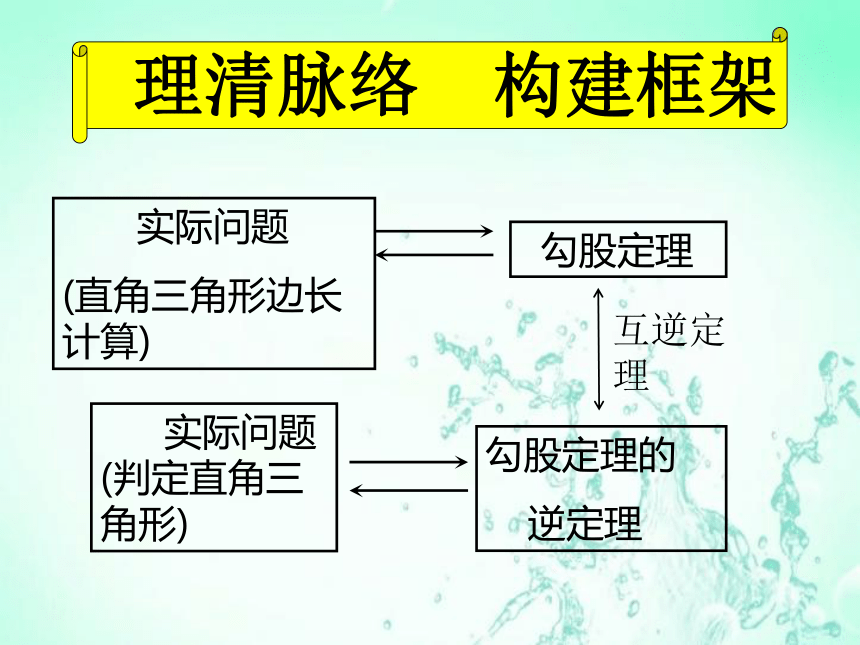
实际问题
(直角三角形边长计算)
勾股定理
勾股定理的
逆定理
实际问题
(判定直角三角形)
互逆定理
理清脉络 构建框架
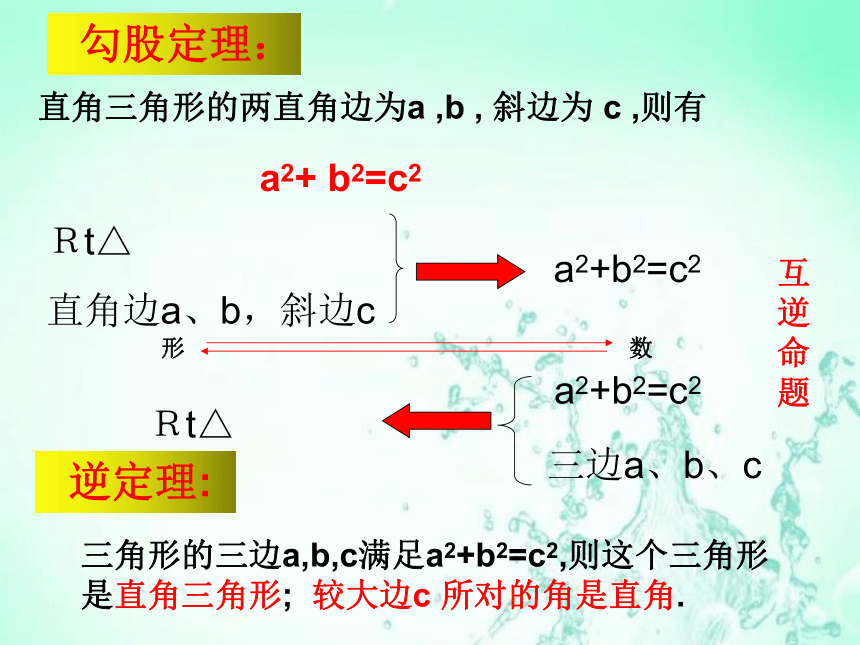
三边a、b、c
a2+b2=c2
形 数
a2+b2=c2
Rt△
直角边a、b,斜边c
Rt△
互逆命题
直角三角形的两直角边为a ,b , 斜边为 c ,则有
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
逆定理:
a2+ b2=c2
勾股定理:
(一)勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
练一练
1.下列说法正确的是( )
A. 若a,b,c是?ABC的三边,则
B. 若a,b,c是Rt△ABC的三边,则
C. 若a,b,c是Rt△ABC的三边, 则
D. 若a,b,c是Rt△ABC的三边, 则
D
基础知识 巩固训练
2. 已知直角三角形的两边长为3、2,则另一条边 长___________.
3.在△ABC中,∠C=90°,
(1)若BC = 5,AC = 12,则 AB= ;
(2)若BC = 3,AB = 5 , 则 AC= ;
4.下图中字母A、B所代表的正方形的面积分别为___________.
13
289 ,25
4
基础知识 巩固训练
(二)勾股定理的逆定理
如果三角形的三边长为a,b,c,满足 _
,那么这个三角形是_____三角形.
练一练
1.下列各组线段中 ,能够组成直角三角形的是(? ).
A 6 , 7 , 8 B 5 , 6 , 7
C 4 , 5 , 6 D 3 , 4 , 5
D
直角
基础知识 巩固训练
2 .已知△ABC中,∠A:∠B:∠C= 1 : 2 : 3 ,
则它的三条边之比为(? ).
A . B .
C . D .
3..木工做一个长方形桌面,量得桌面的长为60cm,宽为32cm,对角线为68cm,这个桌面 ________. (填”合格”或”不合格”).
B
合格
基础知识 巩固训练
(三)原命题、逆命题和逆定理
1、如果两个命题的题设和结论正好 ,那么这样的两个命题叫做 命题.如果把其中一个叫做原命题,那么另一个叫做它的 .
2、如果一个定理的逆命题经过证明是 ,那么它也是一个定理,我们称这两个定理互为逆定理.
相反
互逆
逆命题
正确
基础知识 巩固训练
1.命题“对顶角相等”的逆命题是:
这个命题是 (填成立或不成立).
2.下列各命题的逆命题成立的( )
A. 全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等
D.如果两个角都是45°,那么这两个角相等
成立
如果两个角是对顶角,那么这两个角相等
C
基础知识 巩固训练
(四)勾股数
能够成为_____三角形三条边长的三个________称为勾股数.
练一练
下列几组数中,是勾股数的是( )
A、4,5,6 B、12,16,20
C、-10,24,26 D、2.4,4.5,26.01
直角
正整数
B
基础知识
强化训练
1. 命题“两条直线平行,内错角相等” 的逆命题是 .
3.直角三角形两直角边长分别为5cm, 12cm,则斜边上的高为 .
内错角相等,两直线平行
25或7
2. 一个直角三角形的三边分别为3,4, x, 则 .
4.小华和小红都从同一点O出发,小华向北走9米到A点,小红向东走到B点时,当两人相距为15米,则小红向东走了 米.
5.三角形的三边长a, b, c满足等式
则此三角形是 三角形.
12
直角
强化训练
综合运用 解决问题
A
B
C
H
G
F
B
如图所示,测得长方体的木块长4 cm,宽
3 cm,高4 cm.一只蜘蛛潜伏在木块的一个顶点 A 处,
一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛
究竟应该沿着怎样的路线爬上去,所走的路程会最短,
并求最短路径.
7.如图以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 .
9
强化训练
8.若等边△ABC的边长为2cm,那么△ABC的面积为(? ).
A. B. C. D.
9.三角形的三边长为a,b,c,且满足等式
,则此三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
A
B
强化训练
10.一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距 ( )
A.25 海里 B.30 海里
C.35 海里 D.40 海里
D
强化训练
11.如图,在四边形ABCD中,∠B=90°,AB=BC=4,CD=6,DA=2,求∠DAB的度数.
强化训练
解:
·
强化训练
12.如图△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm,求△DEF的面积.
强化训练
解:
·
强化训练
13.已知如图,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求四边形ABCD的面积.
强化训练
解:
·
强化训练
14.如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长.
能力提升
解:
·
强化训练
能力提升
如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.请问:蚂蚁爬到食物处的最近路线是多长?
A
B
能力提升:
1. 在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
A
用勾股定理解决简单的实际问题
在不是直角三角形中如何求线段长和面积?
解一般三角形的问题常常通过作高转化成直角三角形,利用勾股定理解决问题.
思考:
已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3, 且AB⊥BC.求四边形 ABCD的面积.
分析:本题解题的关键是恰当的添加辅助线,利用勾股定理的逆定理判定△ADC的形状为直角三角形,再利用勾股定理解题.
解:连接AC,∵AB⊥BC,∴∠ABC=90°.
∵在△ABC中,∠ABC=90°,AB=1,BC=2,
∴AC= .∵CD=2,AD=3, ∴△ACD是直角三角形;∴四边形的面积为1+ .
能力提升: 勾股定理及其逆定理的综合应用
如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
变式训练:
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
解:设BE=x,折叠,∴△BCE ≌△FCE,
∴BC=FC=10. 令BE=FE=x,长方形ABCD,
∴ AB=DC=8 ,AD=BC=10,∠D=90°,
∴DF=6, AF=4,∠A=90°, AE=8-x ,
∴ ,解得 x = 5 .∴BE的长为5.
能力提升:会用勾股定理解决较综合的问题
再见
复习与小结
实际问题
(直角三角形边长计算)
勾股定理
勾股定理的
逆定理
实际问题
(判定直角三角形)
互逆定理
理清脉络 构建框架
三边a、b、c
a2+b2=c2
形 数
a2+b2=c2
Rt△
直角边a、b,斜边c
Rt△
互逆命题
直角三角形的两直角边为a ,b , 斜边为 c ,则有
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
逆定理:
a2+ b2=c2
勾股定理:
(一)勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
练一练
1.下列说法正确的是( )
A. 若a,b,c是?ABC的三边,则
B. 若a,b,c是Rt△ABC的三边,则
C. 若a,b,c是Rt△ABC的三边, 则
D. 若a,b,c是Rt△ABC的三边, 则
D
基础知识 巩固训练
2. 已知直角三角形的两边长为3、2,则另一条边 长___________.
3.在△ABC中,∠C=90°,
(1)若BC = 5,AC = 12,则 AB= ;
(2)若BC = 3,AB = 5 , 则 AC= ;
4.下图中字母A、B所代表的正方形的面积分别为___________.
13
289 ,25
4
基础知识 巩固训练
(二)勾股定理的逆定理
如果三角形的三边长为a,b,c,满足 _
,那么这个三角形是_____三角形.
练一练
1.下列各组线段中 ,能够组成直角三角形的是(? ).
A 6 , 7 , 8 B 5 , 6 , 7
C 4 , 5 , 6 D 3 , 4 , 5
D
直角
基础知识 巩固训练
2 .已知△ABC中,∠A:∠B:∠C= 1 : 2 : 3 ,
则它的三条边之比为(? ).
A . B .
C . D .
3..木工做一个长方形桌面,量得桌面的长为60cm,宽为32cm,对角线为68cm,这个桌面 ________. (填”合格”或”不合格”).
B
合格
基础知识 巩固训练
(三)原命题、逆命题和逆定理
1、如果两个命题的题设和结论正好 ,那么这样的两个命题叫做 命题.如果把其中一个叫做原命题,那么另一个叫做它的 .
2、如果一个定理的逆命题经过证明是 ,那么它也是一个定理,我们称这两个定理互为逆定理.
相反
互逆
逆命题
正确
基础知识 巩固训练
1.命题“对顶角相等”的逆命题是:
这个命题是 (填成立或不成立).
2.下列各命题的逆命题成立的( )
A. 全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等
D.如果两个角都是45°,那么这两个角相等
成立
如果两个角是对顶角,那么这两个角相等
C
基础知识 巩固训练
(四)勾股数
能够成为_____三角形三条边长的三个________称为勾股数.
练一练
下列几组数中,是勾股数的是( )
A、4,5,6 B、12,16,20
C、-10,24,26 D、2.4,4.5,26.01
直角
正整数
B
基础知识
强化训练
1. 命题“两条直线平行,内错角相等” 的逆命题是 .
3.直角三角形两直角边长分别为5cm, 12cm,则斜边上的高为 .
内错角相等,两直线平行
25或7
2. 一个直角三角形的三边分别为3,4, x, 则 .
4.小华和小红都从同一点O出发,小华向北走9米到A点,小红向东走到B点时,当两人相距为15米,则小红向东走了 米.
5.三角形的三边长a, b, c满足等式
则此三角形是 三角形.
12
直角
强化训练
综合运用 解决问题
A
B
C
H
G
F
B
如图所示,测得长方体的木块长4 cm,宽
3 cm,高4 cm.一只蜘蛛潜伏在木块的一个顶点 A 处,
一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛
究竟应该沿着怎样的路线爬上去,所走的路程会最短,
并求最短路径.
7.如图以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 .
9
强化训练
8.若等边△ABC的边长为2cm,那么△ABC的面积为(? ).
A. B. C. D.
9.三角形的三边长为a,b,c,且满足等式
,则此三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
A
B
强化训练
10.一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距 ( )
A.25 海里 B.30 海里
C.35 海里 D.40 海里
D
强化训练
11.如图,在四边形ABCD中,∠B=90°,AB=BC=4,CD=6,DA=2,求∠DAB的度数.
强化训练
解:
·
强化训练
12.如图△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm,求△DEF的面积.
强化训练
解:
·
强化训练
13.已知如图,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求四边形ABCD的面积.
强化训练
解:
·
强化训练
14.如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长.
能力提升
解:
·
强化训练
能力提升
如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.请问:蚂蚁爬到食物处的最近路线是多长?
A
B
能力提升:
1. 在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
A
用勾股定理解决简单的实际问题
在不是直角三角形中如何求线段长和面积?
解一般三角形的问题常常通过作高转化成直角三角形,利用勾股定理解决问题.
思考:
已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3, 且AB⊥BC.求四边形 ABCD的面积.
分析:本题解题的关键是恰当的添加辅助线,利用勾股定理的逆定理判定△ADC的形状为直角三角形,再利用勾股定理解题.
解:连接AC,∵AB⊥BC,∴∠ABC=90°.
∵在△ABC中,∠ABC=90°,AB=1,BC=2,
∴AC= .∵CD=2,AD=3, ∴△ACD是直角三角形;∴四边形的面积为1+ .
能力提升: 勾股定理及其逆定理的综合应用
如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
变式训练:
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
解:设BE=x,折叠,∴△BCE ≌△FCE,
∴BC=FC=10. 令BE=FE=x,长方形ABCD,
∴ AB=DC=8 ,AD=BC=10,∠D=90°,
∴DF=6, AF=4,∠A=90°, AE=8-x ,
∴ ,解得 x = 5 .∴BE的长为5.
能力提升:会用勾股定理解决较综合的问题
再见
