人教版九年级上册第23章旋转期末复习课件(17张PPT)
文档属性
| 名称 | 人教版九年级上册第23章旋转期末复习课件(17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 796.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 12:10:52 | ||
图片预览






文档简介
第二十三章旋转
小结复习
专题一:旋转概念及性质
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角.如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.
旋转的性质:
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等.
1.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A.55° B.45° C.40° D.35°
例题讲解和练习
D
2.如图,在△ABC中,将△ABC绕点A顺时针旋转40°后,得到△AB′C′,且C′在边BC上,则∠AC′C的度数为( )
A.80° B.70° C.60° D.50°
B
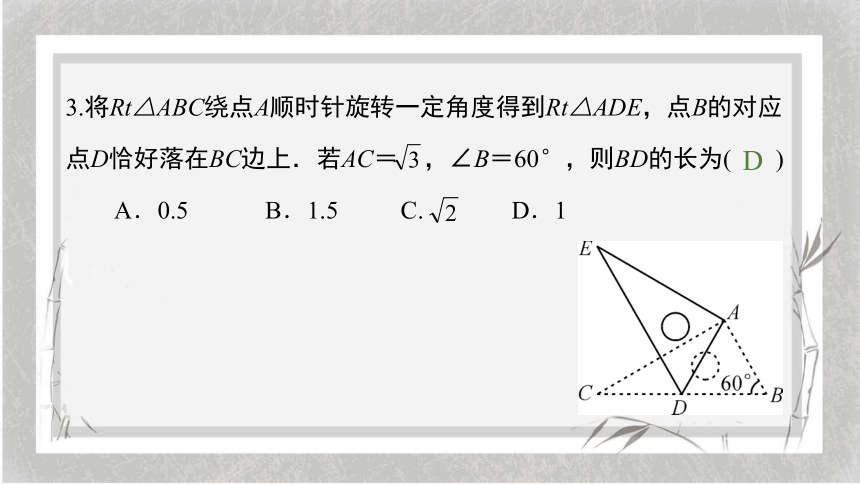
3.将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC= ,∠B=60°,则BD的长为( )
A.0.5 B.1.5 C. D.1
D
专题三:旋转作图
1.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0).
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到点A1与点A2距离之和最小,请直接写出P点的坐标
(1)将△ABC向右平移4个单位长度,得到△A′B′C′
(2)把△A′B′C′绕点C′逆时针旋转90°,得到△A″B″C″
2.如图所示,在正方形网格中,每个小正方形的边长均为1个单位长度
3.在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点分别为A(-4,7),B(-1,8),C(-2,11)
(1)画出△ABC向下平移6个单位长度后的△A1B1C1;
(2)画出△A1B1C1绕原点O顺时针旋转90°后的△A2B2C2,并写出B2,C2的坐标.
把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
专题二:中心对称概念及性质
轴对称图形:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
1.下面的图形中,既是轴对称图形又是中心对称图形的是( )
C
2.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点对称的点为P′(-x,-y).
如:已知点A的坐标为(1,2),则点A关于x轴对称的点的坐标为 ,关于y轴对称的点的坐标为 ,关于原点对称的点的坐标为 .
专题三:关于原点对称的点的坐标
(1,-2)
(-1,2)
(-1,-2)
1.将点P(-2,3)向右平移3个单位长度得到点P1,点P2与点P1关于原点对称,则点P2的坐标是( )
A.(-5,-3) B.(1,-3)
C.(-1,-3) D.(5,-3)
2.已知平面直角坐标系中的点A(3,-5)与点B关于原点中心对称,则点B的坐标为 .
3.若点A(-3,n)在x轴上,则点B(n-1,n+1)关于原点对称的点的坐标为 .
D
(-3,5)
(1,-1)
5.在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若点A(m,1)在y轴上,则点B(m-1,m+1)关于原点对称的点的坐标为 .
(1,-1)
A
1.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).
①将△ABC先向右平移4个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
专题四:中心对称作图
2.如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
小结复习
专题一:旋转概念及性质
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角.如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.
旋转的性质:
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等.
1.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A.55° B.45° C.40° D.35°
例题讲解和练习
D
2.如图,在△ABC中,将△ABC绕点A顺时针旋转40°后,得到△AB′C′,且C′在边BC上,则∠AC′C的度数为( )
A.80° B.70° C.60° D.50°
B
3.将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC= ,∠B=60°,则BD的长为( )
A.0.5 B.1.5 C. D.1
D
专题三:旋转作图
1.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0).
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到点A1与点A2距离之和最小,请直接写出P点的坐标
(1)将△ABC向右平移4个单位长度,得到△A′B′C′
(2)把△A′B′C′绕点C′逆时针旋转90°,得到△A″B″C″
2.如图所示,在正方形网格中,每个小正方形的边长均为1个单位长度
3.在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点分别为A(-4,7),B(-1,8),C(-2,11)
(1)画出△ABC向下平移6个单位长度后的△A1B1C1;
(2)画出△A1B1C1绕原点O顺时针旋转90°后的△A2B2C2,并写出B2,C2的坐标.
把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
专题二:中心对称概念及性质
轴对称图形:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
1.下面的图形中,既是轴对称图形又是中心对称图形的是( )
C
2.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点对称的点为P′(-x,-y).
如:已知点A的坐标为(1,2),则点A关于x轴对称的点的坐标为 ,关于y轴对称的点的坐标为 ,关于原点对称的点的坐标为 .
专题三:关于原点对称的点的坐标
(1,-2)
(-1,2)
(-1,-2)
1.将点P(-2,3)向右平移3个单位长度得到点P1,点P2与点P1关于原点对称,则点P2的坐标是( )
A.(-5,-3) B.(1,-3)
C.(-1,-3) D.(5,-3)
2.已知平面直角坐标系中的点A(3,-5)与点B关于原点中心对称,则点B的坐标为 .
3.若点A(-3,n)在x轴上,则点B(n-1,n+1)关于原点对称的点的坐标为 .
D
(-3,5)
(1,-1)
5.在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若点A(m,1)在y轴上,则点B(m-1,m+1)关于原点对称的点的坐标为 .
(1,-1)
A
1.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).
①将△ABC先向右平移4个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
专题四:中心对称作图
2.如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
同课章节目录
