人教版七年级上册数学3.4实际问题与一元一次方程第1课时 课件(20张ppt)
文档属性
| 名称 | 人教版七年级上册数学3.4实际问题与一元一次方程第1课时 课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 216.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:56:40 | ||
图片预览








文档简介
(共20张PPT)
第三章 一元一次方程
3.4 实际问题与一元一次方程
第1课时 解决实际问题(1)
人教版七年级上册
解下列方程:
一、创设情境,导入新课
解:去括号,得
合并同类项,得
移项,得
系数化为1,得
一、创设情境,导入新课
解:去括号,得
合并同类项,得
移项,得
系数化为1,得
一、创设情境,导入新课
去括号,得
合并同类项,得
移项,得
系数化为1,得
解:去分母(方程两边乘12),得
一、创设情境,导入新课
去括号,得
合并同类项,得
移项,得
系数化为1,得
解:去分母(方程两边乘6),得
一、创设情境,导入新课
二、推进新课
例1 某车间有22名工人,每人每天可以生产
1 200个螺钉或2 000个螺母,1个螺钉需要配
2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
思考1:1个螺钉需要配2个螺母是什么意思?
思考2:题目中包含着怎样的等量关系?
螺母的数量是螺钉数量的2倍
螺母的数量是螺钉数量的2倍
二、推进新课
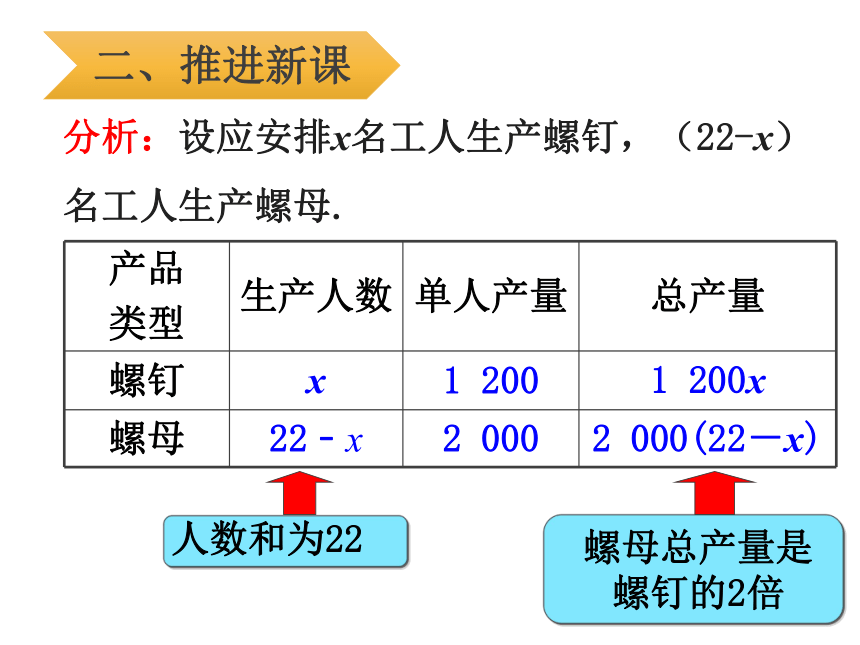
分析:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
产品 类型 生产人数 单人产量 总产量
螺钉 x 1 200 1 200x
螺母 22﹣x 2 000 2 000(22-x)
人数和为22
螺母总产量是螺钉的2倍
二、推进新课
解法一:根据题意,可列方程
2 × 1 200x =2 000(22-x).
去括号,得 2×1 200x=2 000×22-2 000x.
移项及合并同类项,得4 400x=44 000.
系数化为1,得x=10.
22-x=12.
二、推进新课
答:应安排10名工人生产螺钉,12名工人生产螺母.
解法二:根据题意,可列方程
2×1 200x=2 000(22-x).
6x=5(22-x).
解方程,得
6x=5×22-5x.
6x=110-5x.
11x=110.
22-x=12.
二、推进新课
x=10.
答:应安排10名工人生产螺钉,12名工人生产螺母.
例2 整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
二、推进新课
人均 效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
列表分析:
工作量之和等
于总工作量1
二、推进新课
注意:工作量=人均效率×人数×工作时间
解:设安排x人先做4 h.
依题意,得 .
解方程,得4x+8(x+2)=40.
4x+8x+16=40.
12x=24.
x=2.
答:应先安排2人做4 h.
二、推进新课
三、综合应用
1.木器厂加工安排22名工人为某学校制作课桌椅,一名工人每天可加工双人桌18张或单人座椅30把,为了使每天生产的产品刚好配套,应该分配多少名工人加工课桌,多少名工人加工座椅?
解:设应分配x名工人加工课桌,则22-x名工人加工座椅.依题意,可列方程
2 × 18x=30(22-x).
解得x=10.
22-10=12.
答:应分配10名工人加工课桌,12名工人加工座椅.
三、综合应用
2.为庆祝国庆节的到来,七年级(1)班学生接受了制作校旗的任务,原计划一半同学参加制作,每天制作40面.而实际上,在完成了三分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务.假设每人的制作效率相同,问共制作小旗多少面?
三、综合应用
解:设共制作x面校旗.
解得x=180.
答:共制作180面校旗.
依题意,可列方程
三、综合应用
谈谈你的收获和困惑!
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题
的答案
检 验
建模思想
四、小结与作业
作业:习题3.4第2、3、4、5题.
四、小结与作业
第三章 一元一次方程
3.4 实际问题与一元一次方程
第1课时 解决实际问题(1)
人教版七年级上册
解下列方程:
一、创设情境,导入新课
解:去括号,得
合并同类项,得
移项,得
系数化为1,得
一、创设情境,导入新课
解:去括号,得
合并同类项,得
移项,得
系数化为1,得
一、创设情境,导入新课
去括号,得
合并同类项,得
移项,得
系数化为1,得
解:去分母(方程两边乘12),得
一、创设情境,导入新课
去括号,得
合并同类项,得
移项,得
系数化为1,得
解:去分母(方程两边乘6),得
一、创设情境,导入新课
二、推进新课
例1 某车间有22名工人,每人每天可以生产
1 200个螺钉或2 000个螺母,1个螺钉需要配
2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
思考1:1个螺钉需要配2个螺母是什么意思?
思考2:题目中包含着怎样的等量关系?
螺母的数量是螺钉数量的2倍
螺母的数量是螺钉数量的2倍
二、推进新课
分析:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
产品 类型 生产人数 单人产量 总产量
螺钉 x 1 200 1 200x
螺母 22﹣x 2 000 2 000(22-x)
人数和为22
螺母总产量是螺钉的2倍
二、推进新课
解法一:根据题意,可列方程
2 × 1 200x =2 000(22-x).
去括号,得 2×1 200x=2 000×22-2 000x.
移项及合并同类项,得4 400x=44 000.
系数化为1,得x=10.
22-x=12.
二、推进新课
答:应安排10名工人生产螺钉,12名工人生产螺母.
解法二:根据题意,可列方程
2×1 200x=2 000(22-x).
6x=5(22-x).
解方程,得
6x=5×22-5x.
6x=110-5x.
11x=110.
22-x=12.
二、推进新课
x=10.
答:应安排10名工人生产螺钉,12名工人生产螺母.
例2 整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
二、推进新课
人均 效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
列表分析:
工作量之和等
于总工作量1
二、推进新课
注意:工作量=人均效率×人数×工作时间
解:设安排x人先做4 h.
依题意,得 .
解方程,得4x+8(x+2)=40.
4x+8x+16=40.
12x=24.
x=2.
答:应先安排2人做4 h.
二、推进新课
三、综合应用
1.木器厂加工安排22名工人为某学校制作课桌椅,一名工人每天可加工双人桌18张或单人座椅30把,为了使每天生产的产品刚好配套,应该分配多少名工人加工课桌,多少名工人加工座椅?
解:设应分配x名工人加工课桌,则22-x名工人加工座椅.依题意,可列方程
2 × 18x=30(22-x).
解得x=10.
22-10=12.
答:应分配10名工人加工课桌,12名工人加工座椅.
三、综合应用
2.为庆祝国庆节的到来,七年级(1)班学生接受了制作校旗的任务,原计划一半同学参加制作,每天制作40面.而实际上,在完成了三分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务.假设每人的制作效率相同,问共制作小旗多少面?
三、综合应用
解:设共制作x面校旗.
解得x=180.
答:共制作180面校旗.
依题意,可列方程
三、综合应用
谈谈你的收获和困惑!
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题
的答案
检 验
建模思想
四、小结与作业
作业:习题3.4第2、3、4、5题.
四、小结与作业
