人教版七年级数学下册5.2.2平行线的判定 课件(22张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.2.2平行线的判定 课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 720.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 12:12:08 | ||
图片预览





文档简介
5.2.2 平行线的判定
知识回顾:
1、什么叫同位角?内错角?怎样的两个角是同旁内角?
2、判定两条直线平行的方法
同位角:在被截直线同一方向,在截线同侧;
内错角:在被截直线之间,在截线两侧;
同旁内角:在被截直线之间,在截线同侧(旁)。
(1)平行线的定义;
(2)平行公理的推论。
知识回顾:
(1)什么是平行线:
(2)平行线的表示方法:
(3)平行线的画法:
(4)平行线的性质:
同一平面,不相交
如AB//CD
过直线外一点,能且只能
画一条直线与已知直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
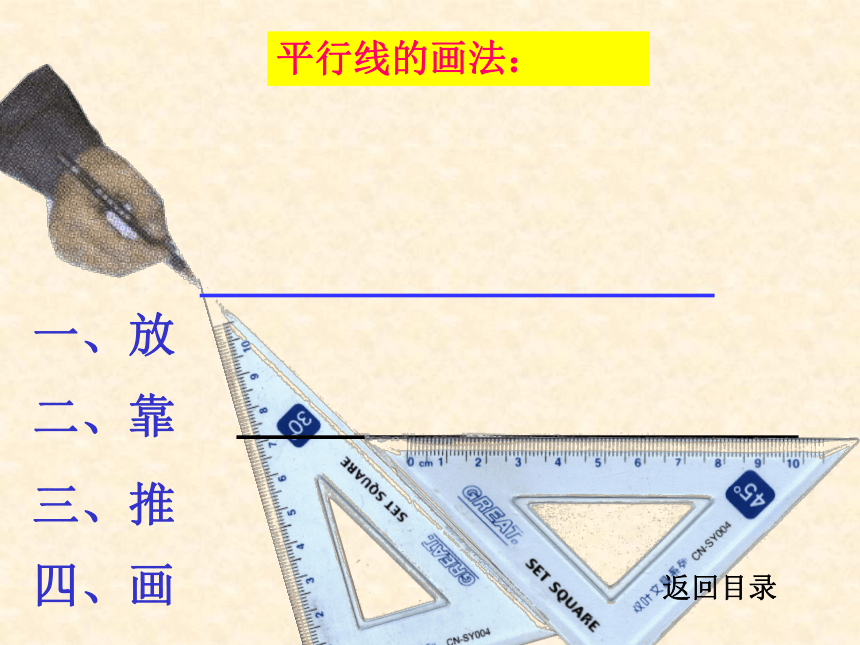
一放,二靠,三推,四画
一、放
二、靠
三、推
四、画
平行线的画法:
返回目录
学习目标
1、进一步理解同位角、内错角、同旁内角的概念及识别方法;
2、掌握利用同位角相等、内错角相等及同旁内角互补判定两条直线平行的方法。
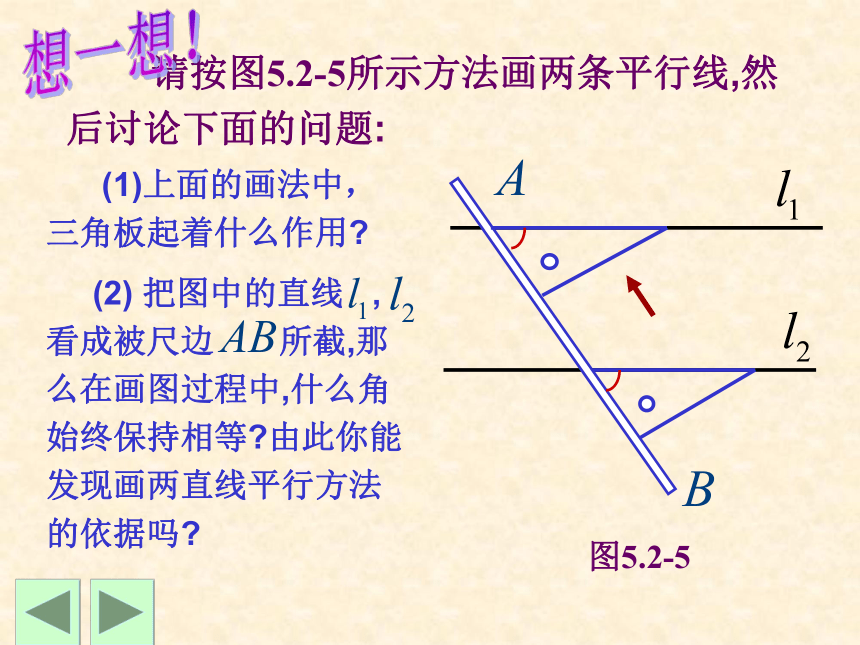
请按图5.2-5所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法中,三角板起着什么作用?
(2) 把图中的直线 , 看成被尺边 所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?
想一想!
图5.2-5
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
平行线判定方法1:
同位角相等,两直线平行。
请记住!
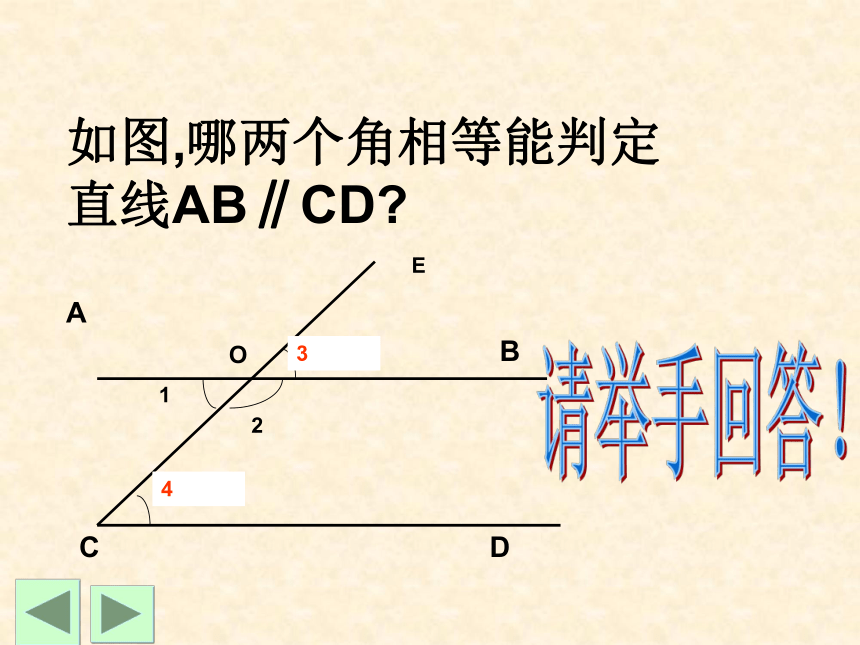
如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
请举手回答!
4
3
E
O
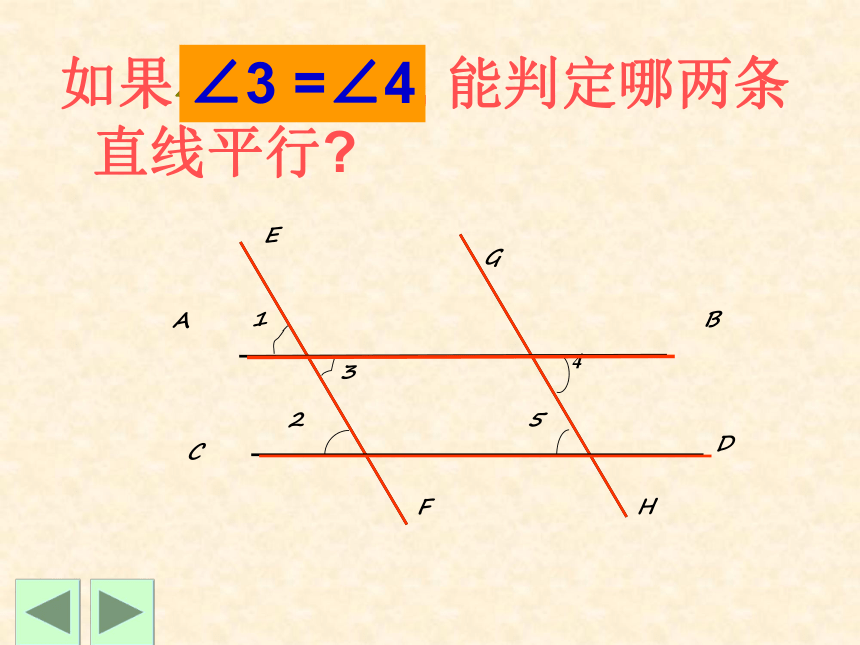
如果 , 能判定哪两条直线平行?
∠1 =∠2
4
1
2
3
A
B
C
E
F
D
5
H
G
∠3 =∠4
如图,已知∠1=∠2,AB与CD平行吗?为什么?
探究1
A
B
C
D
E
F
1
2
3
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
平行线判定方法2:内错角相等,两直线平行。
请记住!
如图,如果∠2+ ∠3=180 o,那么AB∥CD 吗?为什么?
A
B
C
D
F
1
3
2
探究2
因为∠3与_____互补, ∠2与____互补,
∠1
∠3
所以∠1= _____
∠2
所以,AB∥CD
答:如果∠2+ ∠3=180 o,那么AB∥CD,理由如下:
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.
平行线判定方法3:同旁内角互补,两直线平行。
请记住!
思考: 两条直线垂直于同一条直线,这两条直线平行吗?
答:
理由:
a
b
c
1
2
平行
∵b⊥a,c⊥a. (已知)
如图:b⊥a、c⊥a,那么b、c平行吗?
∴∠1=∠2=90o(垂直定义)
∴b∥c.(同位角相等,两直线平行)
同位角相等,两直线平行.
巩固新知,深化理解
1 如图,你能说出木工用图中的角尺画平行线的道理吗?
(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?
巩固新知,深化理解
2、如图, BE是AB的延长线.
答: AD∥BC .根据同位角相等,两直线平行.
1、如图,由 可判断哪两条直线平行?由 ,可判断哪两条直线平行?
跟踪练习:
2、在下列结论给出的条件中,不能判定AB∥DF ( )
A、∠A+ ∠2=1800
B、∠A=∠3
C、∠1=∠4
D、∠1=∠A
A
E
B
D
C
F
1
4
2
3
D
A
B
F
C
D
E
已知∠BAF=500, ∠ACE=1400,CD⊥CE,则有DC∥AB,试说明理由
500
1400
温馨提示:可以采用多种思路说明。
巩固新知,深化理解
3、课本P15 第2、3题
这节课我们学了什么?
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。
你记住了吗?
平行线判定方法:
平行线判定方法4:如果两条直线都和 三条 直线平行,那么这两条直线也互相平行。
平行线判定方法5:如果两条直线垂直于同一条直线,那么这两条直线平行。
平行线判定方法6:平行线的定义。
今天的作业
课本P15
习题5.2
第1题、第4题和第7题
知识回顾:
1、什么叫同位角?内错角?怎样的两个角是同旁内角?
2、判定两条直线平行的方法
同位角:在被截直线同一方向,在截线同侧;
内错角:在被截直线之间,在截线两侧;
同旁内角:在被截直线之间,在截线同侧(旁)。
(1)平行线的定义;
(2)平行公理的推论。
知识回顾:
(1)什么是平行线:
(2)平行线的表示方法:
(3)平行线的画法:
(4)平行线的性质:
同一平面,不相交
如AB//CD
过直线外一点,能且只能
画一条直线与已知直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
一放,二靠,三推,四画
一、放
二、靠
三、推
四、画
平行线的画法:
返回目录
学习目标
1、进一步理解同位角、内错角、同旁内角的概念及识别方法;
2、掌握利用同位角相等、内错角相等及同旁内角互补判定两条直线平行的方法。
请按图5.2-5所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法中,三角板起着什么作用?
(2) 把图中的直线 , 看成被尺边 所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?
想一想!
图5.2-5
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
平行线判定方法1:
同位角相等,两直线平行。
请记住!
如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
请举手回答!
4
3
E
O
如果 , 能判定哪两条直线平行?
∠1 =∠2
4
1
2
3
A
B
C
E
F
D
5
H
G
∠3 =∠4
如图,已知∠1=∠2,AB与CD平行吗?为什么?
探究1
A
B
C
D
E
F
1
2
3
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
平行线判定方法2:内错角相等,两直线平行。
请记住!
如图,如果∠2+ ∠3=180 o,那么AB∥CD 吗?为什么?
A
B
C
D
F
1
3
2
探究2
因为∠3与_____互补, ∠2与____互补,
∠1
∠3
所以∠1= _____
∠2
所以,AB∥CD
答:如果∠2+ ∠3=180 o,那么AB∥CD,理由如下:
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.
平行线判定方法3:同旁内角互补,两直线平行。
请记住!
思考: 两条直线垂直于同一条直线,这两条直线平行吗?
答:
理由:
a
b
c
1
2
平行
∵b⊥a,c⊥a. (已知)
如图:b⊥a、c⊥a,那么b、c平行吗?
∴∠1=∠2=90o(垂直定义)
∴b∥c.(同位角相等,两直线平行)
同位角相等,两直线平行.
巩固新知,深化理解
1 如图,你能说出木工用图中的角尺画平行线的道理吗?
(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?
巩固新知,深化理解
2、如图, BE是AB的延长线.
答: AD∥BC .根据同位角相等,两直线平行.
1、如图,由 可判断哪两条直线平行?由 ,可判断哪两条直线平行?
跟踪练习:
2、在下列结论给出的条件中,不能判定AB∥DF ( )
A、∠A+ ∠2=1800
B、∠A=∠3
C、∠1=∠4
D、∠1=∠A
A
E
B
D
C
F
1
4
2
3
D
A
B
F
C
D
E
已知∠BAF=500, ∠ACE=1400,CD⊥CE,则有DC∥AB,试说明理由
500
1400
温馨提示:可以采用多种思路说明。
巩固新知,深化理解
3、课本P15 第2、3题
这节课我们学了什么?
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。
你记住了吗?
平行线判定方法:
平行线判定方法4:如果两条直线都和 三条 直线平行,那么这两条直线也互相平行。
平行线判定方法5:如果两条直线垂直于同一条直线,那么这两条直线平行。
平行线判定方法6:平行线的定义。
今天的作业
课本P15
习题5.2
第1题、第4题和第7题
