人教版数学八年级上册 15.2.3整数指数幂课件(18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 15.2.3整数指数幂课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 308.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 12:14:44 | ||
图片预览






文档简介
新人教版 · 数学 · 八年级(上)
15.2.3 整数指数幂
数学思考:通过观察、推理、总结得出负整数指数幂的意义。
理解负整数指数幂的意义,熟练运用 整数指数幂运算性质进行运算 。
1.
2.
问题1 正整数指数幂有哪些运算性质呢?
(6) 0指数幂的运算:当a≠0时,a0=1
复习
(1)同底数幂的乘法:am·an=am+n (m、n为正整数)
(2)幂的乘方:(am)n=amn (m、n为正整数)
(3)积的乘方:(ab)n=anbn (m、n为正整数)
(4)同底数幂的除法:am÷an=am-n (a≠0 m、n为正整数且m>n)
(5)分式的乘方: ( b≠0 ,n是正整数)
当m<n时,
探索负整数指数幂的意义
预习导学——不看不讲
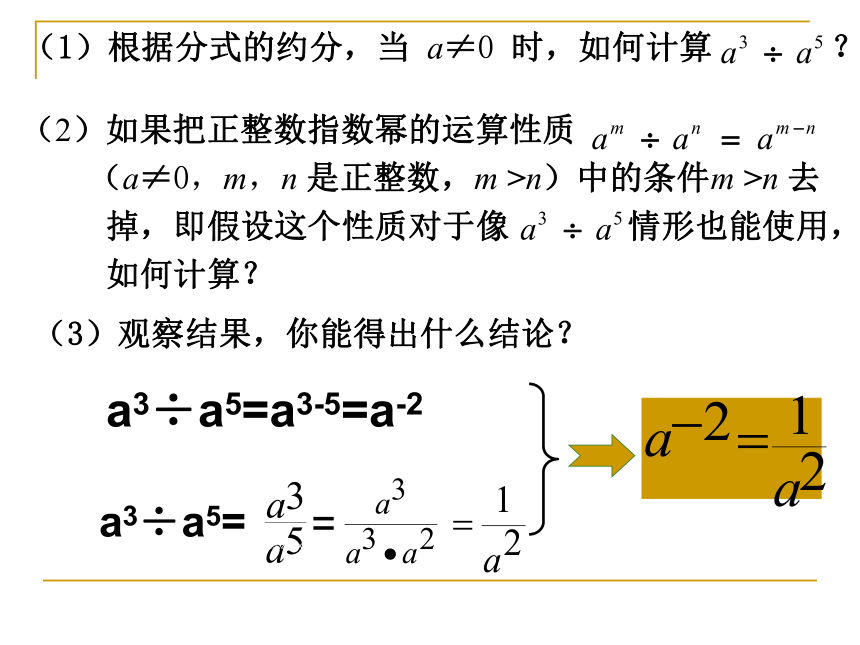
(1)根据分式的约分,当 a≠0 时,如何计算 ?
(2)如果把正整数指数幂的运算性质
(a≠0,m,n 是正整数,m >n)中的条件m >n 去
掉,即假设这个性质对于像 情形也能使用,
如何计算?
a3÷a5=a3-5=a-2
a3÷a5=
=
[来源:z*x*x*k]
(3)观察结果,你能得出什么结论?
引入负整数指数幂后,指数的取值范围就扩大到全体整数。
负整数指数幂的意义:
一般地,当n是正整数时,
这就是说:a-n(a≠0)是an 的倒数
思考1:指数为负数的意思是什么?
思考2:为什么要求a≠0?
填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .
你能记住这些吗?
8
探索整数指数幂的性质
(m,n 是正整数)这条性质能否推广到m,n 是任意整
数的情形?
问题3 引入负整数指数后,
9
归纳:am·an=am+n这条性质对于m,n是任意整数的情形仍然适用。
归纳结论:事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂。
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
(4) ( a≠0 m,n 是整数);
(5) ( b≠0 n 是整数).
问题4 能否将整数指数幂的5条性质进行适当合并?
根据整数指数幂的运算性质,当m,n为整数时,
, ,因此,
,即同底数幂的除法 可以转化
为同底数幂的乘法 .特别地,
所以,
即分式的乘方 可以转化为积的乘方
探索整数指数幂的性质
这样,整数指数幂的运算性质可以归结为:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
合作探究——不议不讲 整数指数幂性质的应用
例9 计算:
解:
解:
例9 计算:
合作探究——不议不讲 整数指数幂性质的应用
(1)
(2)
(4)
(a-b).(a-b) ÷(a-b)
(3)
-
-4
2
导学测评——不练不讲 计算:
小结:
1、负整数指数幂的意义:
2、负整数指数幂的引入,还将指数的取值范围扩大
3、整数指数幂的运算性质。
到了全体整数。
4、谈一谈这节课的收获,你是怎么学的?
布置作业:
1. 课本p147习题15.2第7题
2. 导学测评
勤奋是学习的枝叶,
当然很苦,
智慧是学习的花朵,
当然香郁。
谢谢大家!
再 见!
15.2.3 整数指数幂
数学思考:通过观察、推理、总结得出负整数指数幂的意义。
理解负整数指数幂的意义,熟练运用 整数指数幂运算性质进行运算 。
1.
2.
问题1 正整数指数幂有哪些运算性质呢?
(6) 0指数幂的运算:当a≠0时,a0=1
复习
(1)同底数幂的乘法:am·an=am+n (m、n为正整数)
(2)幂的乘方:(am)n=amn (m、n为正整数)
(3)积的乘方:(ab)n=anbn (m、n为正整数)
(4)同底数幂的除法:am÷an=am-n (a≠0 m、n为正整数且m>n)
(5)分式的乘方: ( b≠0 ,n是正整数)
当m<n时,
探索负整数指数幂的意义
预习导学——不看不讲
(1)根据分式的约分,当 a≠0 时,如何计算 ?
(2)如果把正整数指数幂的运算性质
(a≠0,m,n 是正整数,m >n)中的条件m >n 去
掉,即假设这个性质对于像 情形也能使用,
如何计算?
a3÷a5=a3-5=a-2
a3÷a5=
=
[来源:z*x*x*k]
(3)观察结果,你能得出什么结论?
引入负整数指数幂后,指数的取值范围就扩大到全体整数。
负整数指数幂的意义:
一般地,当n是正整数时,
这就是说:a-n(a≠0)是an 的倒数
思考1:指数为负数的意思是什么?
思考2:为什么要求a≠0?
填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .
你能记住这些吗?
8
探索整数指数幂的性质
(m,n 是正整数)这条性质能否推广到m,n 是任意整
数的情形?
问题3 引入负整数指数后,
9
归纳:am·an=am+n这条性质对于m,n是任意整数的情形仍然适用。
归纳结论:事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂。
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
(4) ( a≠0 m,n 是整数);
(5) ( b≠0 n 是整数).
问题4 能否将整数指数幂的5条性质进行适当合并?
根据整数指数幂的运算性质,当m,n为整数时,
, ,因此,
,即同底数幂的除法 可以转化
为同底数幂的乘法 .特别地,
所以,
即分式的乘方 可以转化为积的乘方
探索整数指数幂的性质
这样,整数指数幂的运算性质可以归结为:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
合作探究——不议不讲 整数指数幂性质的应用
例9 计算:
解:
解:
例9 计算:
合作探究——不议不讲 整数指数幂性质的应用
(1)
(2)
(4)
(a-b).(a-b) ÷(a-b)
(3)
-
-4
2
导学测评——不练不讲 计算:
小结:
1、负整数指数幂的意义:
2、负整数指数幂的引入,还将指数的取值范围扩大
3、整数指数幂的运算性质。
到了全体整数。
4、谈一谈这节课的收获,你是怎么学的?
布置作业:
1. 课本p147习题15.2第7题
2. 导学测评
勤奋是学习的枝叶,
当然很苦,
智慧是学习的花朵,
当然香郁。
谢谢大家!
再 见!
