人教版数学八年级下册课件:17.1-勾股定理(1)(共16张)
文档属性
| 名称 | 人教版数学八年级下册课件:17.1-勾股定理(1)(共16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览




文档简介
第十七章 勾股定理
17.1 勾股定理(1)
1
介绍我国古代在勾股定理研究方面所取得
的成就,激发爱国热情,勤奋学习.
2
一、学习目标
了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理;
二、新课引入
1.回顾直角三角形的有关定义.
2.我们曾经利用图形面积探索过数学公式,大家还记得在哪用过吗?
单项式乘多项式:a(b+c+d)=___________
ab+ac+ad
二、新课引入
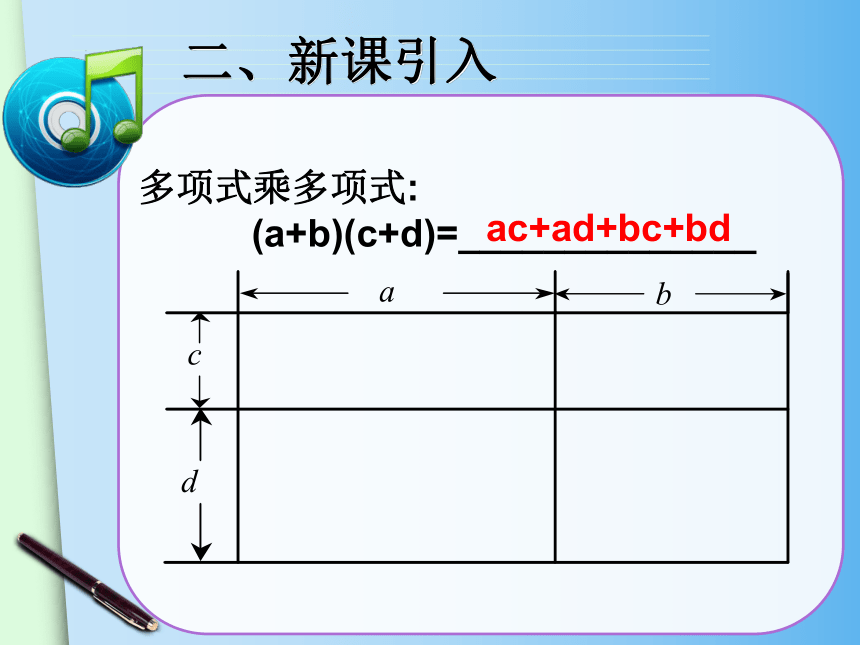
多项式乘多项式:
(a+b)(c+d)=______________
ac+ad+bc+bd
二、新课引入
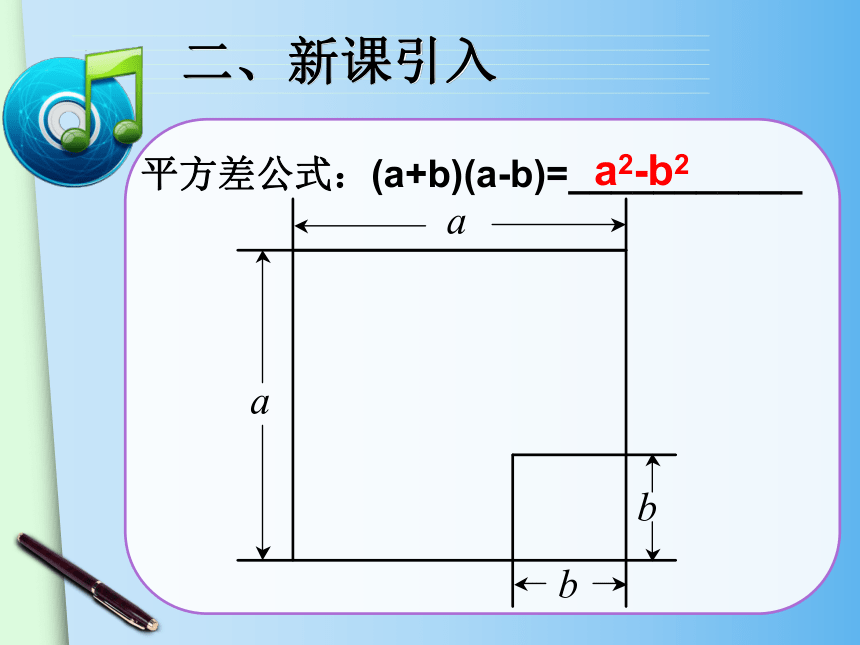
平方差公式:(a+b)(a-b)=___________
a2-b2
二、新课引入
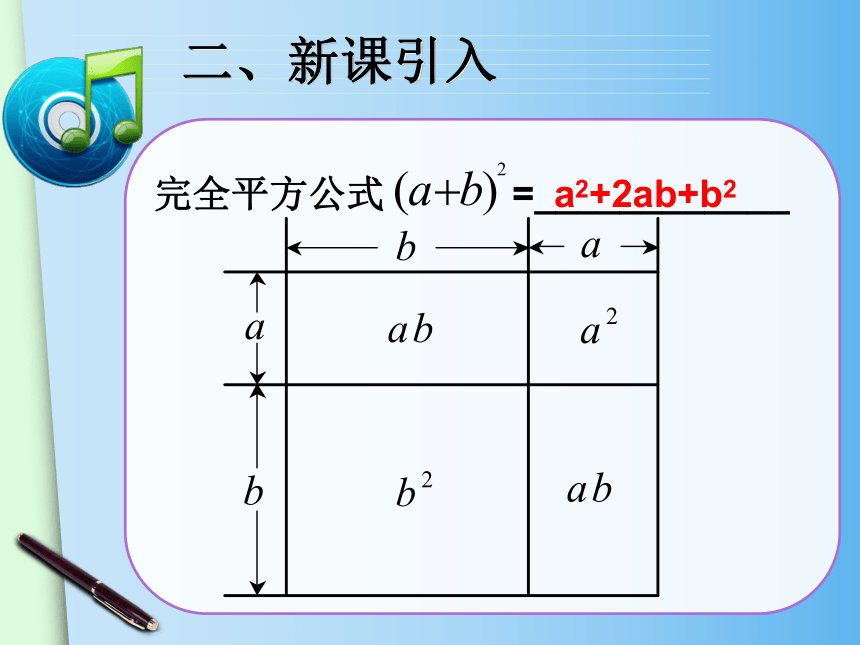
完全平方公式 =____________
a2+2ab+b2
三、自学指导
认真阅读课本第22至24页的内容,完
成下面练习并体验知识点的形成过程.
知识点一勾股定理的探究
1、如图,邮票图案的三个正方形小方格中间是一个直角三角形,如果1个小方格为1个单位面积,那么直角三角形的两直角边长分别是____和____,斜边长是____;
三个正方形的面积分别是_____、_____和____.
4
3
5
16
9
25
三、自学指导
知识点一
2、上题三个正方形面积之间的关系是_________________________________________________________
两个小正方形的面积之和等于大的正方形面积
三、自学指导
知识点一
3、把上题三个正方形的面积关系,转化为直角三角形三边的关系,则得到什么结论?
结论:直角三角形两直角边的________
等于______________________.
?
命题1(勾股定理)如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
平方的和
斜边的平方
a2+b2=c2
四、自学检测
知识点一
练一练 设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:(1)由勾股定理得62+b2=102
∴b=8
(2)由勾股定理得52+122=102
∴c=13
(3)由勾股定理得a2+152=252
∴a=20
a
c
b
五、勾股定理的证明
知识点二勾股定理的证明
1.赵爽弦图利用了_______关系进行勾股定理的证明.
2.剪4个全等的直角三角形,拼成如图图形,其中直角三角形的两直角边分别是a、b,则中间的小正方形的边长为________,利用面积证明勾股定理.
面积
b-a
五、勾股定理的证明
知识点二勾股定理的证明
∵ S大正方形=4S直角三角形+S小正方形
=4×_____+ (____)2
=_____________
=_____________
又∵S大正方形=C2
∴___2+___2=____2
b-a
2ab+b2-2ab+a2
a2 +b2
a
b
c
六、自学检测
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A、B、C、D的边长分别是12,16,9,12,求最大正方形E的面积.
六、自学检测
解:如图所示,正方形A、B、C、D的边长分别是12,16,9,12,设直角三角形H的斜边长为c ,由勾股定理知
122+162=c2
∴c=20 ,即正方形F边长为20
同理可得,正方形G的边长为15
故直角三角形K的两直角边分别为20,15,设它的斜边长为k,由勾股定理知
202+152=k2
∴k=25,即正方形E的边长为25
∴S正方形E=25×25=625
七、当堂训练
1、判断题
(1)若a、b、c是三角形的三边则
( )
(2)直角三角形中,两边的平方和等于第三边 的平方. ( )
2、已知Rt△ABC中,∠C=90°,若BC=4,AC=2,则AB=______;若AB=4,BC=2,则AC=______.
3、阅读课本第30页的内容,了解毕
达哥拉斯和美国总统詹姆斯·加菲尔德
对勾股定理的证法.
X
X
八、归纳小结
1、勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么____________.
2、赵爽弦图利用了_______关系进行勾股定理的证明.
3、学习反思:_____________________________
_____________________________.
a2+b2=c2
面积
17.1 勾股定理(1)
1
介绍我国古代在勾股定理研究方面所取得
的成就,激发爱国热情,勤奋学习.
2
一、学习目标
了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理;
二、新课引入
1.回顾直角三角形的有关定义.
2.我们曾经利用图形面积探索过数学公式,大家还记得在哪用过吗?
单项式乘多项式:a(b+c+d)=___________
ab+ac+ad
二、新课引入
多项式乘多项式:
(a+b)(c+d)=______________
ac+ad+bc+bd
二、新课引入
平方差公式:(a+b)(a-b)=___________
a2-b2
二、新课引入
完全平方公式 =____________
a2+2ab+b2
三、自学指导
认真阅读课本第22至24页的内容,完
成下面练习并体验知识点的形成过程.
知识点一勾股定理的探究
1、如图,邮票图案的三个正方形小方格中间是一个直角三角形,如果1个小方格为1个单位面积,那么直角三角形的两直角边长分别是____和____,斜边长是____;
三个正方形的面积分别是_____、_____和____.
4
3
5
16
9
25
三、自学指导
知识点一
2、上题三个正方形面积之间的关系是_________________________________________________________
两个小正方形的面积之和等于大的正方形面积
三、自学指导
知识点一
3、把上题三个正方形的面积关系,转化为直角三角形三边的关系,则得到什么结论?
结论:直角三角形两直角边的________
等于______________________.
?
命题1(勾股定理)如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
平方的和
斜边的平方
a2+b2=c2
四、自学检测
知识点一
练一练 设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:(1)由勾股定理得62+b2=102
∴b=8
(2)由勾股定理得52+122=102
∴c=13
(3)由勾股定理得a2+152=252
∴a=20
a
c
b
五、勾股定理的证明
知识点二勾股定理的证明
1.赵爽弦图利用了_______关系进行勾股定理的证明.
2.剪4个全等的直角三角形,拼成如图图形,其中直角三角形的两直角边分别是a、b,则中间的小正方形的边长为________,利用面积证明勾股定理.
面积
b-a
五、勾股定理的证明
知识点二勾股定理的证明
∵ S大正方形=4S直角三角形+S小正方形
=4×_____+ (____)2
=_____________
=_____________
又∵S大正方形=C2
∴___2+___2=____2
b-a
2ab+b2-2ab+a2
a2 +b2
a
b
c
六、自学检测
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A、B、C、D的边长分别是12,16,9,12,求最大正方形E的面积.
六、自学检测
解:如图所示,正方形A、B、C、D的边长分别是12,16,9,12,设直角三角形H的斜边长为c ,由勾股定理知
122+162=c2
∴c=20 ,即正方形F边长为20
同理可得,正方形G的边长为15
故直角三角形K的两直角边分别为20,15,设它的斜边长为k,由勾股定理知
202+152=k2
∴k=25,即正方形E的边长为25
∴S正方形E=25×25=625
七、当堂训练
1、判断题
(1)若a、b、c是三角形的三边则
( )
(2)直角三角形中,两边的平方和等于第三边 的平方. ( )
2、已知Rt△ABC中,∠C=90°,若BC=4,AC=2,则AB=______;若AB=4,BC=2,则AC=______.
3、阅读课本第30页的内容,了解毕
达哥拉斯和美国总统詹姆斯·加菲尔德
对勾股定理的证法.
X
X
八、归纳小结
1、勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么____________.
2、赵爽弦图利用了_______关系进行勾股定理的证明.
3、学习反思:_____________________________
_____________________________.
a2+b2=c2
面积
