人教版数学九年级上册第22章二次函数期末复习课件(51张)
文档属性
| 名称 | 人教版数学九年级上册第22章二次函数期末复习课件(51张) |  | |
| 格式 | ppt | ||
| 文件大小 | 989.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 17:45:36 | ||
图片预览









文档简介
第二十二章二次函数
期末考试复习
二次函数
概念
二次函数的图像与性质
二次函数的实际应用
二次函数与一次函数
专题一:二次函数概念
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫二次函数
x是自变量,a是二次项系数;b是一次项系数;c是常数项.
2.下列函数中,是二次函数的为( )
A.y=ax3+x2+bx+c(a≠0) B.
C.y=(x+1)2-x2 D.y=x(1-x)
D
1.在下列函数中,y是x的二次函数的是( )
A.y=2x+1 B.
C.y=x2-3 D.y=(k-1)x2+3x-1
C
练习:二次函数概念
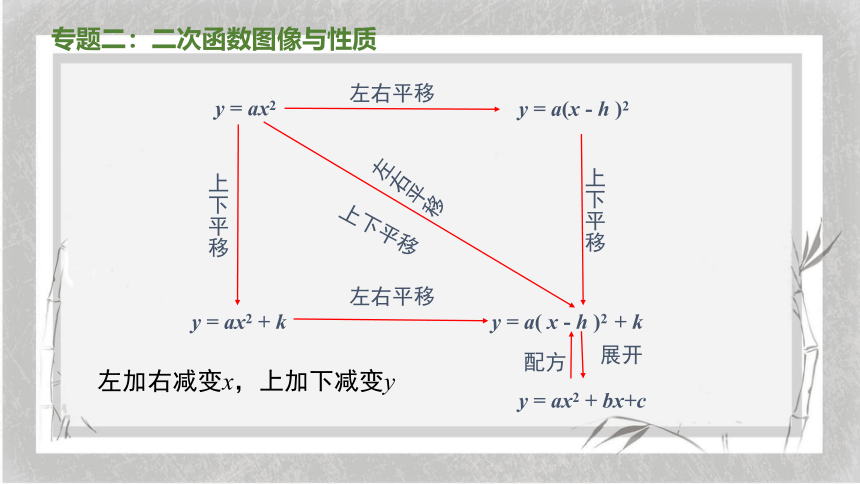
专题二:二次函数图像与性质
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
上下平移
左右平移
y = ax2 + bx+c
展开
左加右减变x,上加下减变y
配方
例题讲解和练习
1.将抛物线y=x2向右平移2个单位长度,再向上平移3个单位长度后,平移后的抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x-2)2+3
C.y=(x+2)2-3 D.y=(x-2)2-3
2.要得到抛物线y=2(x-3)2-2,可将抛物线y=2x2( )
A.先向左平移3个单位长度,再向上平移2个单位长度
B.先向左平移3个单位长度,再向下平移2个单位长度
C.先向右平移3个单位长度,再向下平移2个单位长度
D.先向右平移3个单位长度,再向上平移2个单位长度
B
A
3.将抛物线y=x2+2x-3向左平移2个单位长度后,得到新抛物线的解析式为( )
A.y=(x-3)2+1 B.y=(x-1)2+1
C.y=(x+1)2+3 D.y=(x+3)2-4
D
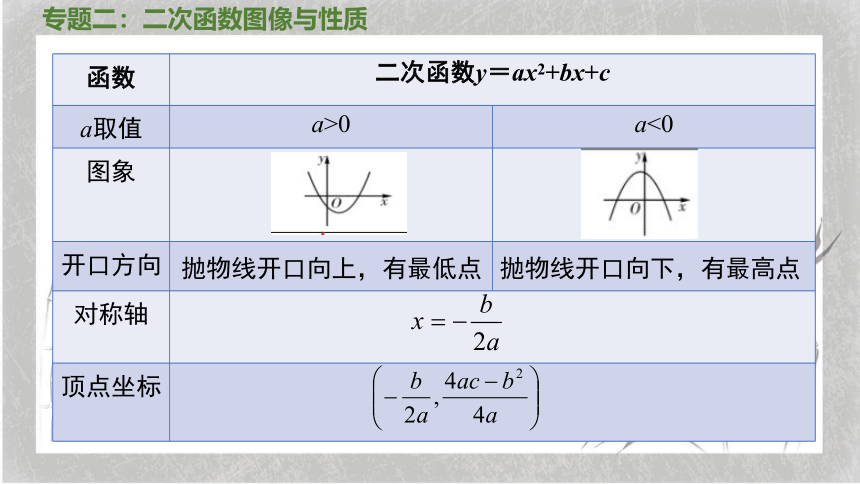
专题二:二次函数图像与性质
函数
二次函数y=ax2+bx+c
a取值
a>0
a<0
图象
开口方向
对称轴
顶点坐标
抛物线开口向上,有最低点
抛物线开口向下,有最高点
函数
二次函数y=ax2+bx+c
a取值
a>0
a<0
增减性
最值
减小
减小
增大
增大
例题讲解和练习
1.抛物线y=(x-1)2+2的顶点坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
A
2.抛物线y=x2-2x+3的顶点坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
A
3.对于y=2(x+1)2-3的图象,下列叙述错误的是( )
A.顶点坐标为(-1,-3) B.对称轴为直线x=-1
C.当x<-1时y随x的增大而减小 D.函数有最大值3
D
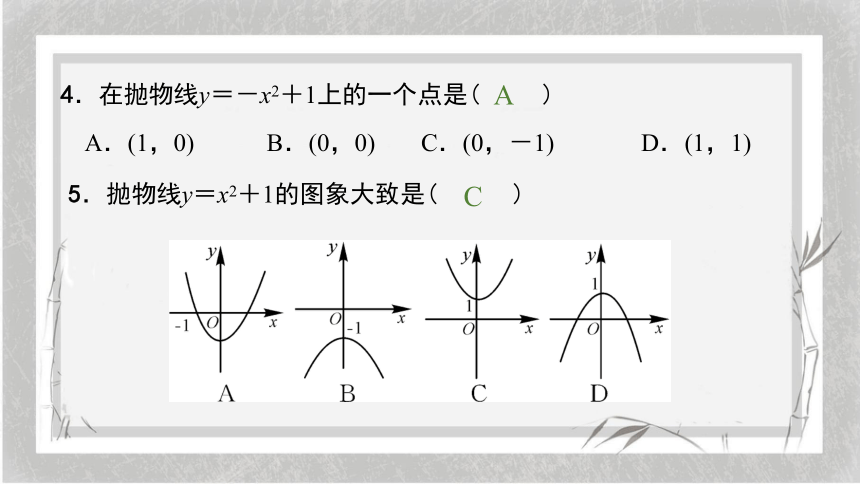
4.在抛物线y=-x2+1上的一个点是( )
A.(1,0) B.(0,0) C.(0,-1) D.(1,1)
5.抛物线y=x2+1的图象大致是( )
A
C
6.在平面直角坐标系中,下列函数的图象经过原点的是( )
A.y=-2x+1 B.y=-2(x-1)
C.y=-x+k(k>0) D.y=-x2
7.若二次函数y=ax2(a>0)的图象过点(3,4),则其图象一定经过点( )
A.(3,-4) B.(-3,-4) C.(-3,4) D.(4,3)
8.已知抛物线y=5x2过A(-3,y1),B(2,y2)两点,则下列关系式一定正确的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y2>y1>0
D
C
C
9.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2
C.y3>y2>y1 D.y3>y1>y2
A
10.若二次函数y=x2-6x+c的图象过A(-1,y1),B(2,y2),
C(3,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2
C.y2>y1>y3 D.y3>y1>y2
A
专题三:二次函数与一次函数
抛物线y=ax2+bx+c的图象判断字母系数a,b,c之间的关系
开口方向
a>0
开口向上
a<0
开口向下
对称轴位置
b=0
过原点
a与b同号
与y轴交于正半轴
a与b异号
与y轴交于负半轴
与y轴交点
c=0
对称轴为y轴
c>0
对称轴在y轴左侧
c<0
对称轴在y轴右侧
抛物线y=ax2+bx+c的图象判断字母系数a,b,c之间的关系
与x轴交点
b2-4ac=0
与x轴有唯一交点
b2-4ac>0
与x轴有两个交点
b2-4ac<0
与x轴没有交点
判断a,b,c相关的常见代数式与0的大小关系
a+b+c或a-b+c
令x=1或-1,看函数值
4a+2b+c或4a-2b+c
令x=2或-2,看函数值
9a+3b+c或9a-3b+c
令x=3或-3,看函数值
2a+b
看对称轴与直线x=1的位置
2a-b
看对称轴与直线x=-1的位置
1.在平面直角坐标系中,二次函数 的图象可能是( )
练习:二次函数与一次函数
D
B
2.在同一平面直角坐标系中,一次函数y=ax+c和二次函数
y=a(x+c)2的图象大致为( )
3.在同一平面直角坐标系中,一次函数y=ax+b与二次函数y=ax2-b的图象可能是( )
D
4.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图1所示,下列说法正确的是( )
A.abc<0,b2-4ac>0 B.abc>0,b2-4ac>0
C.abc<0,b2-4ac<0 D.abc>0,b2-4ac<0
B
图1
5.已知二次函数y=ax2+bx+c的图象如图2所示,则下列说法正确的是( )
A.ac<0 B.b<0 C.b2-4ac<0 D.a+b+c<0
图2
B
6.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;
③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的个数是( )
A.4个 3个 C.2个 D.1个
B
7.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
C
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2>4ac,②abc<0,③2a+b-c>0,④a+b+c<0.其中正确的是( )
A.①④ B.②④ C.②③ D.①②③④
A
专题四:用待定系数法求二次函数
1.一个二次函数的图象经过A(-2,4),B(-1,-1),C(0,1)三点,求这个二次函数的解析式
依据题意得
解:设二次函数解析式为y=ax2+bx+c
解得
∴二次函数解析式为
2.如图,抛物线y=x2+bx+c与x轴交于A,B两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
解:∵抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点
解得
∴抛物线解析式为
(1)
(2)
抛物线对称轴为直线x=1;顶点坐标为(1,-4)
专题五:二次函数与几何图形综合
1.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于
点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
解:(1)∵抛物线顶点坐标为A(1,4)
∴设y=a(x-1)2+4
∵抛物线过点B(0,3)
∴3=a(0-1)2+4,解得a=-1.
∴抛物线的解析式为y=-(x-1)2+4
即y=-x2+2x+3.
(2)作点B关于x轴的对称点E(0,-3),连接AE交x轴于点P, 此时,PA+PB的值最小.
设直线AE的解析式为y=kx+b,则
∴直线AE的解析式为y=7x-3
解得
2.如图,抛物线 与x轴交于A,B两点,与y轴交于点C,点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
理由如下:令 ,
解得x1=3,x2=-2.
解:存在.
∴A点坐标为(-2,0).
连接AD,交对称轴于点P,则P为所求的点.
设直线AD的解析式为y=kx+t.将点A,D坐标代入,得
解得
∴直线AD的解析式为
∵对称轴为直线
将
代入
,
得
∴点P的坐标为
3.如图,二次函数y=-x2+mx+n的图象经过点A(-1,4),
B(1,0), 经过点B,且与二次函数y=-x2+mx+n交于点D.
(1)求二次函数的解析式;
(2)点N是二次函数图象上一点(点N在BD上方),过点N作NP⊥x轴,垂足为P,交BD于点M,求MN的最大值.
解:(1)∵二次函数y=-x2+mx+n的图象经过点A(-1,4)、 B(1,0)
∴二次函数的解析式为y=-x2-2x+3.
解得
经过点B
解得
∴一次函数的解析式为
∴MN的最大值为
设
,则
(2)
4.如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;
(3)点F在抛物线的对称轴上运动,是否存在点F,使△BFC的面积为4?如果存在,求出点F的坐标;如果不存在,请说明理由.
解:(1)把A(0,3),B(-1,0)代入y=ax2+2x+c,得
解得
∴抛物线的解析式为y=-x2+2x+3
(2)∵y=-x2+2x+3=-(x-1)2+4
∴D(1,4)
(3)存在.
∵抛物线的对称轴为直线x=1,B(-1,0)
∴C(3,0)
设F(1,m)
∵△BFC的面积为4
∴|m|=2,解得m=2或m=-2.
∴点F的坐标为(1,2)或(1,-2).
5.如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,-3).
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P,使△ABP的面积为10,求点P的坐标.
解:(1)把A(0,3),B(-1,0)代入y=ax2+2x+c,得
解得
∴抛物线的解析式为y=-x2+2x+3
当n=-5时,m2+2m-3=-5,则方程无解
综上,点P的坐标为(-4,5)或(2,5).
(2)∵当y=0时,x2+2x-3=0.
解得x1=-3,x2=1.
∴A(1,0),B(-3,0).
∴AB=4.
设点P的坐标为(m,n).
∵△ABP的面积为10,
解得n=±5.
当n=5时,
解得m=-4或2,∴P(-4,5)或(2,5)
专题六:二次函数实际应用
1.某超市销售一种商品,成本为40元/kg,规定每千克的售价不低于成本,且不高于70元.经市场调查,每天的销售量y(kg)与售价x(元/kg)满足一次函数关系,部分数据如下表:
售价x(元/kg)
50
60
70
销售量y(kg)
90
60
30
(1)求y与x之间的函数解析式;
(2)设商品每天的总利润为W(元),求W与x之间的函数解析式;(利润=收入-成本)
(3)试说明(2)中利润W随售价x的变化而变化的情况,并指出售价为多少时获得最大利润,最大利润是多少?
(2)由题意可得:W=(x-40)(-3x+240)=-3x2+360x-9600.
(3)W=-3x2+360x-9600=-3(x-60)2+1200(40≤x≤70),
当x=60时,W取得最大值,此时W=1200.
答:当售价为60元/kg时获得最大利润,最大利润是1200元.
解:(1)设y与x之间的函数解析式为y=kx+b, 由已知得
解得
即y与x之间的函数解析式是y=-3x+240
2.东风市场经营某种新型电子产品,购进时的价格为20元/件,根据市场预测,在一段时间内,销售价格为40元/件时,销售量为200件,销售单价每降低1元,就可多售出20件.
(1)写出销售量y(件)与销售单价x(元)之间的函数关系式;
(2)写出销售该产品所获利润W(元)与销售单价x(元)之间的函数关系式,并求出市场获得的最大利润;
(3)若市场想获得不低于4000元的利润,同时要完成不少于320件的该产品销售任务,该市场应该如何确定销售价格?
解:(1)y=200+20(40-x)=1000-20x.
(2)W=(x-20)(1000-20x)
=-20x2+1400x-20000
=-20(x-35)2+4500.
当x=35时,W有最大值,为4500.
∴商场获得的最大利润是4500元.
(3)1000-20x≥320,解得x≤34.
当W=4000时,(x-20)(1000-20x)=4000,
解得x1=30,x2=40.
∵对于W与x的函数关系,a=-20<0,
∴当30≤x≤40时,商场销售利润不低于4000元.
又∵x≤34,
∴当30≤x≤34时,
商场获得不低于4000元的利润,同时完成不少于320件的该产品销售任务.
3.一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件,为提高利益,就对该T恤进行涨价销售,经过调查发现,每涨价1元,每周要少卖出10件,请确定该T恤涨价后每周销售利润y(元)与销售单价x(元)之间的函数关系式,并求出销售单价定为多少元时,每周的销售利润最大?
解:y=(x-40)[300-10(x-60)]
=-10x2+1300x-36 000
=-10(x-65)2+6250.
∵x-60≥0且300-10(x-60)≥0,
∴60≤x≤90.
∴当x=65时,y的值最大.
答:销售单价定为65元时,每周的销售利润最大.
4.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1 600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
解:(1)设每件衬衫应降价x元,则每件盈利(44-x)元,
每天可以售出(20+5x).由题意,得
(44-x)(20+5x)=1 600,即(x-4)(x-36)=0.
解得x1=4,x2=36.
为了扩大销售量,增加盈利,尽快减少库存,所以x的值应为36.
答:每件衬衫应降价36元.
(2)设商场平均每天盈利y元,每件衬衫应降价x元,
由题意,得
y=(44-x)(20+5x)
=-5(x-20)2+2880,
∴当x=20时,该函数取得最大值2880元.
答:每件衬衫应降价20元,盈利最大是2880元.
期末考试复习
二次函数
概念
二次函数的图像与性质
二次函数的实际应用
二次函数与一次函数
专题一:二次函数概念
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫二次函数
x是自变量,a是二次项系数;b是一次项系数;c是常数项.
2.下列函数中,是二次函数的为( )
A.y=ax3+x2+bx+c(a≠0) B.
C.y=(x+1)2-x2 D.y=x(1-x)
D
1.在下列函数中,y是x的二次函数的是( )
A.y=2x+1 B.
C.y=x2-3 D.y=(k-1)x2+3x-1
C
练习:二次函数概念
专题二:二次函数图像与性质
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
上下平移
左右平移
y = ax2 + bx+c
展开
左加右减变x,上加下减变y
配方
例题讲解和练习
1.将抛物线y=x2向右平移2个单位长度,再向上平移3个单位长度后,平移后的抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x-2)2+3
C.y=(x+2)2-3 D.y=(x-2)2-3
2.要得到抛物线y=2(x-3)2-2,可将抛物线y=2x2( )
A.先向左平移3个单位长度,再向上平移2个单位长度
B.先向左平移3个单位长度,再向下平移2个单位长度
C.先向右平移3个单位长度,再向下平移2个单位长度
D.先向右平移3个单位长度,再向上平移2个单位长度
B
A
3.将抛物线y=x2+2x-3向左平移2个单位长度后,得到新抛物线的解析式为( )
A.y=(x-3)2+1 B.y=(x-1)2+1
C.y=(x+1)2+3 D.y=(x+3)2-4
D
专题二:二次函数图像与性质
函数
二次函数y=ax2+bx+c
a取值
a>0
a<0
图象
开口方向
对称轴
顶点坐标
抛物线开口向上,有最低点
抛物线开口向下,有最高点
函数
二次函数y=ax2+bx+c
a取值
a>0
a<0
增减性
最值
减小
减小
增大
增大
例题讲解和练习
1.抛物线y=(x-1)2+2的顶点坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
A
2.抛物线y=x2-2x+3的顶点坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
A
3.对于y=2(x+1)2-3的图象,下列叙述错误的是( )
A.顶点坐标为(-1,-3) B.对称轴为直线x=-1
C.当x<-1时y随x的增大而减小 D.函数有最大值3
D
4.在抛物线y=-x2+1上的一个点是( )
A.(1,0) B.(0,0) C.(0,-1) D.(1,1)
5.抛物线y=x2+1的图象大致是( )
A
C
6.在平面直角坐标系中,下列函数的图象经过原点的是( )
A.y=-2x+1 B.y=-2(x-1)
C.y=-x+k(k>0) D.y=-x2
7.若二次函数y=ax2(a>0)的图象过点(3,4),则其图象一定经过点( )
A.(3,-4) B.(-3,-4) C.(-3,4) D.(4,3)
8.已知抛物线y=5x2过A(-3,y1),B(2,y2)两点,则下列关系式一定正确的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y2>y1>0
D
C
C
9.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2
C.y3>y2>y1 D.y3>y1>y2
A
10.若二次函数y=x2-6x+c的图象过A(-1,y1),B(2,y2),
C(3,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2
C.y2>y1>y3 D.y3>y1>y2
A
专题三:二次函数与一次函数
抛物线y=ax2+bx+c的图象判断字母系数a,b,c之间的关系
开口方向
a>0
开口向上
a<0
开口向下
对称轴位置
b=0
过原点
a与b同号
与y轴交于正半轴
a与b异号
与y轴交于负半轴
与y轴交点
c=0
对称轴为y轴
c>0
对称轴在y轴左侧
c<0
对称轴在y轴右侧
抛物线y=ax2+bx+c的图象判断字母系数a,b,c之间的关系
与x轴交点
b2-4ac=0
与x轴有唯一交点
b2-4ac>0
与x轴有两个交点
b2-4ac<0
与x轴没有交点
判断a,b,c相关的常见代数式与0的大小关系
a+b+c或a-b+c
令x=1或-1,看函数值
4a+2b+c或4a-2b+c
令x=2或-2,看函数值
9a+3b+c或9a-3b+c
令x=3或-3,看函数值
2a+b
看对称轴与直线x=1的位置
2a-b
看对称轴与直线x=-1的位置
1.在平面直角坐标系中,二次函数 的图象可能是( )
练习:二次函数与一次函数
D
B
2.在同一平面直角坐标系中,一次函数y=ax+c和二次函数
y=a(x+c)2的图象大致为( )
3.在同一平面直角坐标系中,一次函数y=ax+b与二次函数y=ax2-b的图象可能是( )
D
4.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图1所示,下列说法正确的是( )
A.abc<0,b2-4ac>0 B.abc>0,b2-4ac>0
C.abc<0,b2-4ac<0 D.abc>0,b2-4ac<0
B
图1
5.已知二次函数y=ax2+bx+c的图象如图2所示,则下列说法正确的是( )
A.ac<0 B.b<0 C.b2-4ac<0 D.a+b+c<0
图2
B
6.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;
③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的个数是( )
A.4个 3个 C.2个 D.1个
B
7.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
C
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2>4ac,②abc<0,③2a+b-c>0,④a+b+c<0.其中正确的是( )
A.①④ B.②④ C.②③ D.①②③④
A
专题四:用待定系数法求二次函数
1.一个二次函数的图象经过A(-2,4),B(-1,-1),C(0,1)三点,求这个二次函数的解析式
依据题意得
解:设二次函数解析式为y=ax2+bx+c
解得
∴二次函数解析式为
2.如图,抛物线y=x2+bx+c与x轴交于A,B两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
解:∵抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点
解得
∴抛物线解析式为
(1)
(2)
抛物线对称轴为直线x=1;顶点坐标为(1,-4)
专题五:二次函数与几何图形综合
1.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于
点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
解:(1)∵抛物线顶点坐标为A(1,4)
∴设y=a(x-1)2+4
∵抛物线过点B(0,3)
∴3=a(0-1)2+4,解得a=-1.
∴抛物线的解析式为y=-(x-1)2+4
即y=-x2+2x+3.
(2)作点B关于x轴的对称点E(0,-3),连接AE交x轴于点P, 此时,PA+PB的值最小.
设直线AE的解析式为y=kx+b,则
∴直线AE的解析式为y=7x-3
解得
2.如图,抛物线 与x轴交于A,B两点,与y轴交于点C,点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
理由如下:令 ,
解得x1=3,x2=-2.
解:存在.
∴A点坐标为(-2,0).
连接AD,交对称轴于点P,则P为所求的点.
设直线AD的解析式为y=kx+t.将点A,D坐标代入,得
解得
∴直线AD的解析式为
∵对称轴为直线
将
代入
,
得
∴点P的坐标为
3.如图,二次函数y=-x2+mx+n的图象经过点A(-1,4),
B(1,0), 经过点B,且与二次函数y=-x2+mx+n交于点D.
(1)求二次函数的解析式;
(2)点N是二次函数图象上一点(点N在BD上方),过点N作NP⊥x轴,垂足为P,交BD于点M,求MN的最大值.
解:(1)∵二次函数y=-x2+mx+n的图象经过点A(-1,4)、 B(1,0)
∴二次函数的解析式为y=-x2-2x+3.
解得
经过点B
解得
∴一次函数的解析式为
∴MN的最大值为
设
,则
(2)
4.如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;
(3)点F在抛物线的对称轴上运动,是否存在点F,使△BFC的面积为4?如果存在,求出点F的坐标;如果不存在,请说明理由.
解:(1)把A(0,3),B(-1,0)代入y=ax2+2x+c,得
解得
∴抛物线的解析式为y=-x2+2x+3
(2)∵y=-x2+2x+3=-(x-1)2+4
∴D(1,4)
(3)存在.
∵抛物线的对称轴为直线x=1,B(-1,0)
∴C(3,0)
设F(1,m)
∵△BFC的面积为4
∴|m|=2,解得m=2或m=-2.
∴点F的坐标为(1,2)或(1,-2).
5.如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,-3).
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P,使△ABP的面积为10,求点P的坐标.
解:(1)把A(0,3),B(-1,0)代入y=ax2+2x+c,得
解得
∴抛物线的解析式为y=-x2+2x+3
当n=-5时,m2+2m-3=-5,则方程无解
综上,点P的坐标为(-4,5)或(2,5).
(2)∵当y=0时,x2+2x-3=0.
解得x1=-3,x2=1.
∴A(1,0),B(-3,0).
∴AB=4.
设点P的坐标为(m,n).
∵△ABP的面积为10,
解得n=±5.
当n=5时,
解得m=-4或2,∴P(-4,5)或(2,5)
专题六:二次函数实际应用
1.某超市销售一种商品,成本为40元/kg,规定每千克的售价不低于成本,且不高于70元.经市场调查,每天的销售量y(kg)与售价x(元/kg)满足一次函数关系,部分数据如下表:
售价x(元/kg)
50
60
70
销售量y(kg)
90
60
30
(1)求y与x之间的函数解析式;
(2)设商品每天的总利润为W(元),求W与x之间的函数解析式;(利润=收入-成本)
(3)试说明(2)中利润W随售价x的变化而变化的情况,并指出售价为多少时获得最大利润,最大利润是多少?
(2)由题意可得:W=(x-40)(-3x+240)=-3x2+360x-9600.
(3)W=-3x2+360x-9600=-3(x-60)2+1200(40≤x≤70),
当x=60时,W取得最大值,此时W=1200.
答:当售价为60元/kg时获得最大利润,最大利润是1200元.
解:(1)设y与x之间的函数解析式为y=kx+b, 由已知得
解得
即y与x之间的函数解析式是y=-3x+240
2.东风市场经营某种新型电子产品,购进时的价格为20元/件,根据市场预测,在一段时间内,销售价格为40元/件时,销售量为200件,销售单价每降低1元,就可多售出20件.
(1)写出销售量y(件)与销售单价x(元)之间的函数关系式;
(2)写出销售该产品所获利润W(元)与销售单价x(元)之间的函数关系式,并求出市场获得的最大利润;
(3)若市场想获得不低于4000元的利润,同时要完成不少于320件的该产品销售任务,该市场应该如何确定销售价格?
解:(1)y=200+20(40-x)=1000-20x.
(2)W=(x-20)(1000-20x)
=-20x2+1400x-20000
=-20(x-35)2+4500.
当x=35时,W有最大值,为4500.
∴商场获得的最大利润是4500元.
(3)1000-20x≥320,解得x≤34.
当W=4000时,(x-20)(1000-20x)=4000,
解得x1=30,x2=40.
∵对于W与x的函数关系,a=-20<0,
∴当30≤x≤40时,商场销售利润不低于4000元.
又∵x≤34,
∴当30≤x≤34时,
商场获得不低于4000元的利润,同时完成不少于320件的该产品销售任务.
3.一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件,为提高利益,就对该T恤进行涨价销售,经过调查发现,每涨价1元,每周要少卖出10件,请确定该T恤涨价后每周销售利润y(元)与销售单价x(元)之间的函数关系式,并求出销售单价定为多少元时,每周的销售利润最大?
解:y=(x-40)[300-10(x-60)]
=-10x2+1300x-36 000
=-10(x-65)2+6250.
∵x-60≥0且300-10(x-60)≥0,
∴60≤x≤90.
∴当x=65时,y的值最大.
答:销售单价定为65元时,每周的销售利润最大.
4.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1 600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
解:(1)设每件衬衫应降价x元,则每件盈利(44-x)元,
每天可以售出(20+5x).由题意,得
(44-x)(20+5x)=1 600,即(x-4)(x-36)=0.
解得x1=4,x2=36.
为了扩大销售量,增加盈利,尽快减少库存,所以x的值应为36.
答:每件衬衫应降价36元.
(2)设商场平均每天盈利y元,每件衬衫应降价x元,
由题意,得
y=(44-x)(20+5x)
=-5(x-20)2+2880,
∴当x=20时,该函数取得最大值2880元.
答:每件衬衫应降价20元,盈利最大是2880元.
同课章节目录
