湘教版七年级数学上册第3章一元一次方程的解法和应用课件(42张)
文档属性
| 名称 | 湘教版七年级数学上册第3章一元一次方程的解法和应用课件(42张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 17.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览









文档简介
1.进一步理解一元一次方程及有关概念;
2.掌握等式的基本性质;
3.掌握一元一次方程的解法,能熟练地解方程;
4.掌握建立一元一次方程模型解决实际问题的步骤,
能熟练地解答各类问题;
5.增强数学模型意识,体会数学与生活的联系。
【填空】
1. 只含有一个未知数并且未知数的系数是1的方程
叫做 。
2. 能使方程左、右两边相等的 叫做
方程的解。
?一元一次方程及方程的解的概念
一元一次方程
未知数的值
下列式子是一元一次方程的是 ( )
A. B.
C. D.
若关于x的方程 有一个根是2,
则k的值是 ( )
A. 4 B. -4 C. 5 D. -5
B
A
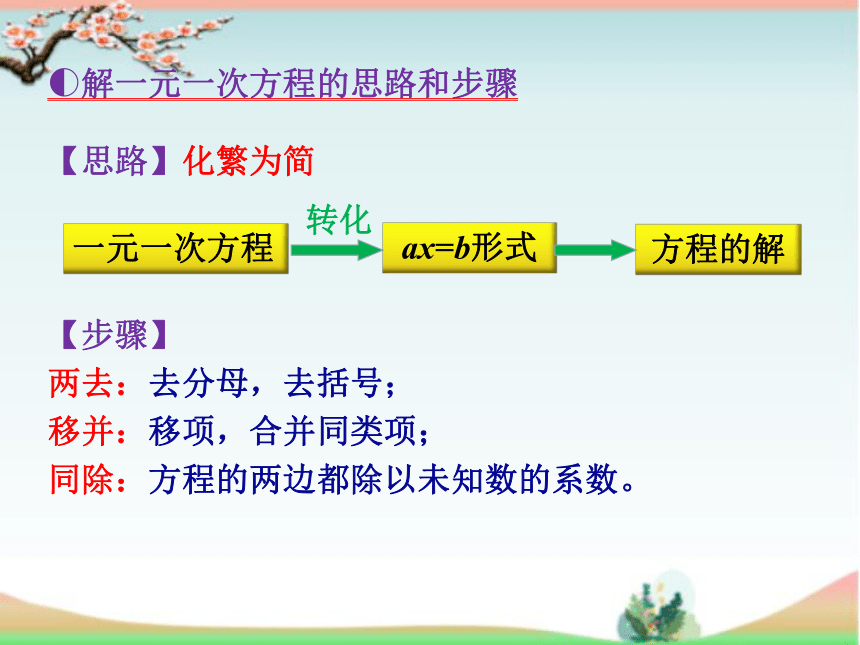
?解一元一次方程的思路和步骤
转化
【思路】化繁为简
【步骤】
两去:去分母,去括号;
移并:移项,合并同类项;
同除:方程的两边都除以未知数的系数。
解方程:
去分母,得
7x=9,
去括号,得
移项,合并同类项得
5(3x-1)-2(2-x)=10x,
15x-5-4+2x=10,
两边都除以7,得
因此原方程的解是
解:
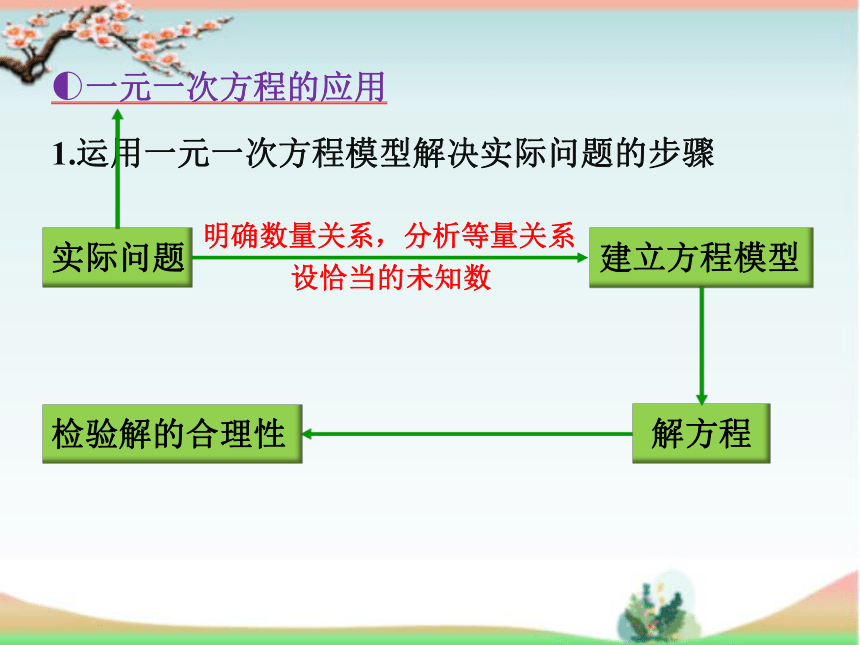
?一元一次方程的应用
1.运用一元一次方程模型解决实际问题的步骤
明确数量关系,分析等量关系
设恰当的未知数
2. 常见类型及其数量关系、等量关系
◆和差倍分问题◆
甲数量+乙数量=总数量
甲数量=乙数量×倍数(或分率、百分率)
甲数量-乙数量=相差量
甲数量=乙数量
和差倍分关系是基本的等量关系,在各类问题中,有特定的数量关系,但等量关系仍然是和差倍分关系。
姜叔叔平时做点蔬菜小买卖,有一天他到蔬菜批发市场用210元采购了黄瓜和豆角共80kg。下表是当天黄瓜的批发价是2元/kg,豆角的批发价是3元/kg,
姜叔叔这天采购了黄瓜和豆角各多少千克?
本题涉及的等量关系是:
采购黄瓜的钱+采购豆角的钱=210元
设采购黄瓜xkg,则采购豆角(80-x)kg,
根据题意得 2x+3(80-x)=210
解得 x=30.
答:姜叔叔这天采购了黄瓜30kg,豆角50kg.
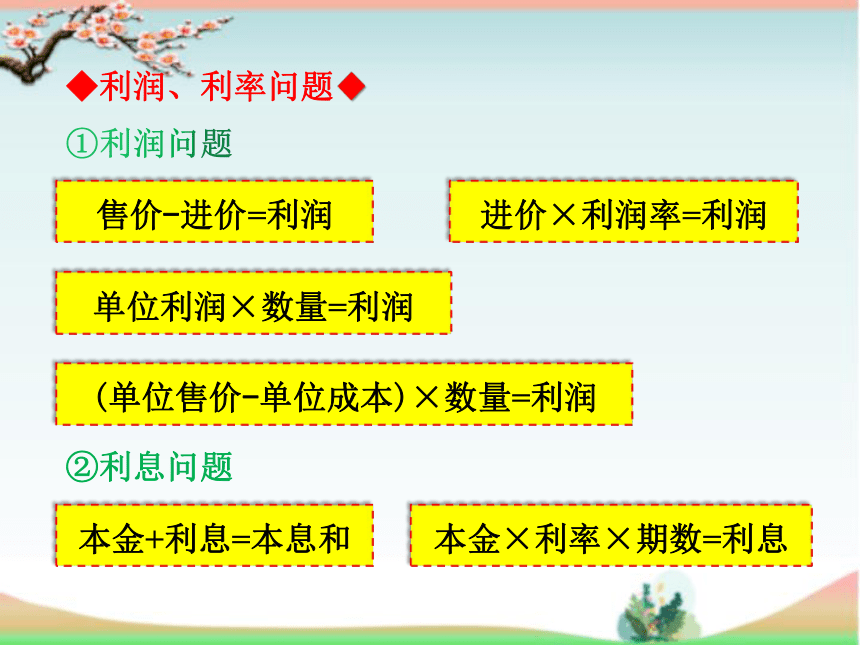
◆利润、利率问题◆
售价-进价=利润
单位利润×数量=利润
进价×利润率=利润
(单位售价-单位成本)×数量=利润
②利息问题
本金+利息=本息和
本金×利率×期数=利息
某公司将40万元分别存入甲、乙两家银行.存入甲银行的存款年利率为5.5%,存入乙银行的存款年利率为4.5%,到期后两笔存款一共可获利息19500元(没交利息税)。试问该公司存入甲、乙两家银行的存款分别是多少元?
本题涉及的等量关系是:
存入甲银行利息+存入乙银行利息=共得利息
设存入甲银行的存款为x万元,根据题意得
解得 x=15.
故存入甲、乙两银行的分别存款为15万元,25万元.
美美电器举行优惠大酬宾活动:把一款洗衣机先按原标价提高30%,再打八折销售,结果每台洗衣机比原来多赚了100元,这款洗衣机原价是多少元?
本题涉及的等量关系是:
售价-原标价=多赚利润
设洗衣机的原标价是x元,根据题意得
解得 x=2500.
◆行程问题◆
速度×时间=路程
甲行路程+乙行路程=全程
追赶的路程=被追者行走路程+相差路程
相遇问题:
基本数量关系:
追及问题:
航行问题:
顺水(风)航速=静水(风)航速+水(风)速
逆水(风)航速=静水(风)航速-水(风)速
甲、乙两站相距270km,一辆快车由甲站开出,每小时行驶70km,同时,一辆慢车由乙站开出,每小时行驶52km,两车同向而行,结果两车同时到达丙站。求乙、丙两站的距离及它们到达丙站所花的时间。
甲
乙
丙
本题是行程问题,基本数量关系是:
速度×时间=路程
本题又是追及问题,涉及的等量关系是:
快车追及路程=慢车所走路程+相距路程
设它们到达丙站所花的时间x小时,
根据题意得
解得 x=15.
则 70x-270=70×15-270=780.
故乙、丙两站距离780km,到达丙站时间为15小时。
◆工程问题◆
工作效率×工作时间=工作量
特点:
基本数量关系:
工作总量可以看作单位“1”
工作效率
=
1
工作时间
常见等量关系:
甲完成的工作量+乙完成的工作量=合作的工作量
一项工作,甲单独做需要12天完成,乙甲单独做需要18天完成.现由甲单独做3天,再由两人合作。试问合作多少天后,可以完成这项工作?
本题涉及的等量关系是:
甲做的工作量+乙做的工作量=总工作量1
设合作x天可以完成任务,根据题意得
解得 x=5.
答:合作5天后可以完成任务.
◆植树问题◆
间隔数=应植树棵数 (只有两端都植树);
间隔数=应植树棵数+1 (两端都不植树).
路长:
间隔数=应植树棵数-1 (两端都植树);
间隔数:
路长=间隔长×间隔数
◆分段收费问题◆
收费单价×数量=总价
标准内费用+超过部分费用=总费用
◆方案问题◆
① 比较方案的结果,进行方案优选。
② 根据方案之间的等量关系,求方案中的数量。
分两种情况:
某保险公司推出一种10年期储蓄性保险。被保险人有两种投保方案:① 一次性投保,到期后获得的保险金是保险费金额的3倍;②分三个年度平均投保,到期后获得的保险金为方案①的80%.如果张某用方案①投保,到期后获得的保险金比方案②多3.2万元,那么张某投保的保险费是多少?
本题涉及的等量关系是:
方案①可获保险金-方案①可获保险金=3.2万元
请同学们自己列方程解答
●A组基础题
1、判断(正确的画“√” ,错误的画“×”)
(1)若a=b,则 a+2c=b+2c; ( )
(3)若a=b,则 a?=b?; ( )
(2)若a=b,则 ; ( )
(4)若ac=bc,则a=b. ( )
√
×
√
×
2. 解方程:
(1)5x-3=-x+3; (2)4y-7=6y-9;
(3)5(x-1)=3(x+1); (4)
3.列方程求解:
(1)当t取何值时,代数式4(1-2t)与代数式t+1的值相等?
(2)当y取何值时,代数式2(3y-1)与代数式3(2-y)的值少5?
4. 计算一种小麦磨成面粉后,质量减少15%,
为了得到7 650 kg面粉,需要多少千克小麦?
5. 到2011年底,我国风力发电装机容量为4500万千瓦,比2005年底的43倍还多6.5万千瓦。求2005底我国风力发电装机容量是多少?
6. 甲、乙、丙3家单位为希望工程共捐款176万元,所捐款数的比为2∶3∶4,问3家单位各捐款多少万元?
本题涉及的等量关系是:
耕了第二天后剩下的亩数=38亩
设这片地有x亩,根据题意得
解得 x=114.
答:这片土地一共有114亩.
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁。
——程大位《直指算法统宗》
意思是:有100个和尚分100个馒头,如果大和尚一人分3个,小和尚3人分一个,正好分完。试问大、小和尚各多少人?
9. 某人骑自行车到工厂上班,若每小时骑15km,则可早到10min;若每小时骑12km,则迟到5min.求他家到工厂的路程。
路程
12
-
路程
15
=
本题涉及的等量关系是:
10.如图,已知某长方体的展开图面积为310cm?,
求x.
本题涉及的等量关系是:
各个面的面积之和=展开图面积.
11.小丽每天要在7∶50之前赶到距家1 000m的学校上学。一天,小丽以0.8m/s的速度出发,5min后,小丽的爸爸发现她忘了带数学书.于是,爸爸立即以1.2m/s的速度去追小丽,并且在途中追上了她。
(1)爸爸追上小丽用了多长时间?
(2)追上小丽时,距离学校还有多远?
本题涉及的等量关系是:
爸爸所追路程=小丽所走路程.
12.已知y=-x?+(a-1)x+2a+3,当x=-1时,y=0.
(1)求a的值;
(2)当x=1时,求y的值.
●B组提高题
(1)将x=-1,y=0代入y=-x?+(a-1)x+2a+3,得到
关于a的一元一次方程,解之,即得a的值;
(2)将(1)求得的a的值及x=1,同时代入
y=-x?+(a-1)x+2a+3,即可求出y的值.
13.解下列方程:
不漏乘,去括号后各项的符号
14. 已知x=2是方程4(x-m)=x+2m的解,求m的值。
15. 方程2(1-x)=x-1的解与方程 的解
相同,求m的值.
先解方程2(1-x)=x-1,再将求得的x值代入方程 ,即可求出m的值.
16. 要配制含盐6%的盐水700g,已有含盐5%的盐水
200g,还需要加入含盐8%的盐水及水各多少克?
本题涉及的等量关系是:
5%盐水含盐g+8%盐水含盐g=7%盐水含盐g
本题还涉及的等量关系:
5%盐水g+8%盐水g+加水g=7%盐水g
17. 两个长方形的长与宽的比都是2∶1,大长方形的宽比小长方形的宽多3cm,大长方形的周长是小长方形的周长的2倍,求这两个长方形的面积.
【思路】求出两个长方形的长与宽,即可求两个长方形的面积.
【等量关系】大长方形周长是小长方形周长的2倍.
【解】设小长方形的宽为xcm,则长为2xcm;大长
方形的宽为(x+3)cm,长为2(x+3)cm.
根据题意得
2[(x+3)+2(x+3)]=2?2(x+2x)
解得 x=3.
所以小长方形的面积为:
3×6=18(cm?) .
大长方形的面积为:
6×9=54(cm?) .
18.要建一个长方形花圃,为了节约材料,花圃的一边靠着已建好的墙,其它三边用总长为70m的栅栏围成.现在甲、乙两人各设计了一个方案:甲的方案是长比宽多10m;乙的方案是长比宽多4m.已知墙长28m,问谁的方案比较符合实际?为什么?
本题涉及的等量关系为:
花圃的长+花圃的宽的2倍=栅栏总长70m.
“符合实际”的意思是设计的长方形花圃的长不超过墙长28m。
解:甲的方案:设花圃的宽为xm,则长为(x+10)m.
根据题意得 (x+10)+2x=70
解得 x=20.
乙的方案:设花圃的宽为ym,则长为(y+4)m.
根据题意得 (x+4)+2x=70
解得 x=22.
则长为20+10=30,而30>28,不符合实际。
则长为22+4=26,而26<28,符合实际。
综上所述,乙的方案比较符合实际。
●C组综合题
19. 足球的表面由白块和黑块组成.已知黑块是五边形,白块是六边形,且每一白块的6条边中,有三条边与黑块相接,另三边与白块相接,每一黑块的五边全与白块的边相接。已知黑块总数是12,求白块数.
从图可以看出,每个白块的三条边分别与黑块的5条边相接. 因此可得本题涉及的等量关系为
所有白块边数的一半=所有黑块的边数
解:设白块数为x,根据题意得
解得 x=20.
答:白块数为20.
20. 5名老师带领若干名学生旅游(旅游费统一支付),他们联系了标价相同的两家旅行社,经洽谈,A旅行社给的优惠条件是教师全部付费,学生按七折付费;B旅行社给的优惠条件是全体师生按八折付费.
(1)学生有多少人时,两家旅行社收费相等?
(2)现有学生20人,那么他们选哪一家旅行社费
用少些呢?
(1)题涉及的等量关系是:
A旅行社的收费=B旅行社的收费
(2)通过计算两家旅行社的收费,并比较收费多少,
确定所选旅行社。
解:(1)设标价为a元,学生有x人,根据题意得
5a+0.7ax=0.8a(x+5)
即 5+0.7x=0.8(x+5)
解得 x=10.
答:当学生是10人时,两家旅行社收费相同.
(2) 当学生是20人时,
A旅行社收费为:5a+20×0.7a=19a.
B旅行社收费为:(20+5)×0.8a=20a.
因为 a>0,
所以 19a-20a=-a<0, 即19a<20a.
所以,他们选A家旅行社费 用少些。
2.掌握等式的基本性质;
3.掌握一元一次方程的解法,能熟练地解方程;
4.掌握建立一元一次方程模型解决实际问题的步骤,
能熟练地解答各类问题;
5.增强数学模型意识,体会数学与生活的联系。
【填空】
1. 只含有一个未知数并且未知数的系数是1的方程
叫做 。
2. 能使方程左、右两边相等的 叫做
方程的解。
?一元一次方程及方程的解的概念
一元一次方程
未知数的值
下列式子是一元一次方程的是 ( )
A. B.
C. D.
若关于x的方程 有一个根是2,
则k的值是 ( )
A. 4 B. -4 C. 5 D. -5
B
A
?解一元一次方程的思路和步骤
转化
【思路】化繁为简
【步骤】
两去:去分母,去括号;
移并:移项,合并同类项;
同除:方程的两边都除以未知数的系数。
解方程:
去分母,得
7x=9,
去括号,得
移项,合并同类项得
5(3x-1)-2(2-x)=10x,
15x-5-4+2x=10,
两边都除以7,得
因此原方程的解是
解:
?一元一次方程的应用
1.运用一元一次方程模型解决实际问题的步骤
明确数量关系,分析等量关系
设恰当的未知数
2. 常见类型及其数量关系、等量关系
◆和差倍分问题◆
甲数量+乙数量=总数量
甲数量=乙数量×倍数(或分率、百分率)
甲数量-乙数量=相差量
甲数量=乙数量
和差倍分关系是基本的等量关系,在各类问题中,有特定的数量关系,但等量关系仍然是和差倍分关系。
姜叔叔平时做点蔬菜小买卖,有一天他到蔬菜批发市场用210元采购了黄瓜和豆角共80kg。下表是当天黄瓜的批发价是2元/kg,豆角的批发价是3元/kg,
姜叔叔这天采购了黄瓜和豆角各多少千克?
本题涉及的等量关系是:
采购黄瓜的钱+采购豆角的钱=210元
设采购黄瓜xkg,则采购豆角(80-x)kg,
根据题意得 2x+3(80-x)=210
解得 x=30.
答:姜叔叔这天采购了黄瓜30kg,豆角50kg.
◆利润、利率问题◆
售价-进价=利润
单位利润×数量=利润
进价×利润率=利润
(单位售价-单位成本)×数量=利润
②利息问题
本金+利息=本息和
本金×利率×期数=利息
某公司将40万元分别存入甲、乙两家银行.存入甲银行的存款年利率为5.5%,存入乙银行的存款年利率为4.5%,到期后两笔存款一共可获利息19500元(没交利息税)。试问该公司存入甲、乙两家银行的存款分别是多少元?
本题涉及的等量关系是:
存入甲银行利息+存入乙银行利息=共得利息
设存入甲银行的存款为x万元,根据题意得
解得 x=15.
故存入甲、乙两银行的分别存款为15万元,25万元.
美美电器举行优惠大酬宾活动:把一款洗衣机先按原标价提高30%,再打八折销售,结果每台洗衣机比原来多赚了100元,这款洗衣机原价是多少元?
本题涉及的等量关系是:
售价-原标价=多赚利润
设洗衣机的原标价是x元,根据题意得
解得 x=2500.
◆行程问题◆
速度×时间=路程
甲行路程+乙行路程=全程
追赶的路程=被追者行走路程+相差路程
相遇问题:
基本数量关系:
追及问题:
航行问题:
顺水(风)航速=静水(风)航速+水(风)速
逆水(风)航速=静水(风)航速-水(风)速
甲、乙两站相距270km,一辆快车由甲站开出,每小时行驶70km,同时,一辆慢车由乙站开出,每小时行驶52km,两车同向而行,结果两车同时到达丙站。求乙、丙两站的距离及它们到达丙站所花的时间。
甲
乙
丙
本题是行程问题,基本数量关系是:
速度×时间=路程
本题又是追及问题,涉及的等量关系是:
快车追及路程=慢车所走路程+相距路程
设它们到达丙站所花的时间x小时,
根据题意得
解得 x=15.
则 70x-270=70×15-270=780.
故乙、丙两站距离780km,到达丙站时间为15小时。
◆工程问题◆
工作效率×工作时间=工作量
特点:
基本数量关系:
工作总量可以看作单位“1”
工作效率
=
1
工作时间
常见等量关系:
甲完成的工作量+乙完成的工作量=合作的工作量
一项工作,甲单独做需要12天完成,乙甲单独做需要18天完成.现由甲单独做3天,再由两人合作。试问合作多少天后,可以完成这项工作?
本题涉及的等量关系是:
甲做的工作量+乙做的工作量=总工作量1
设合作x天可以完成任务,根据题意得
解得 x=5.
答:合作5天后可以完成任务.
◆植树问题◆
间隔数=应植树棵数 (只有两端都植树);
间隔数=应植树棵数+1 (两端都不植树).
路长:
间隔数=应植树棵数-1 (两端都植树);
间隔数:
路长=间隔长×间隔数
◆分段收费问题◆
收费单价×数量=总价
标准内费用+超过部分费用=总费用
◆方案问题◆
① 比较方案的结果,进行方案优选。
② 根据方案之间的等量关系,求方案中的数量。
分两种情况:
某保险公司推出一种10年期储蓄性保险。被保险人有两种投保方案:① 一次性投保,到期后获得的保险金是保险费金额的3倍;②分三个年度平均投保,到期后获得的保险金为方案①的80%.如果张某用方案①投保,到期后获得的保险金比方案②多3.2万元,那么张某投保的保险费是多少?
本题涉及的等量关系是:
方案①可获保险金-方案①可获保险金=3.2万元
请同学们自己列方程解答
●A组基础题
1、判断(正确的画“√” ,错误的画“×”)
(1)若a=b,则 a+2c=b+2c; ( )
(3)若a=b,则 a?=b?; ( )
(2)若a=b,则 ; ( )
(4)若ac=bc,则a=b. ( )
√
×
√
×
2. 解方程:
(1)5x-3=-x+3; (2)4y-7=6y-9;
(3)5(x-1)=3(x+1); (4)
3.列方程求解:
(1)当t取何值时,代数式4(1-2t)与代数式t+1的值相等?
(2)当y取何值时,代数式2(3y-1)与代数式3(2-y)的值少5?
4. 计算一种小麦磨成面粉后,质量减少15%,
为了得到7 650 kg面粉,需要多少千克小麦?
5. 到2011年底,我国风力发电装机容量为4500万千瓦,比2005年底的43倍还多6.5万千瓦。求2005底我国风力发电装机容量是多少?
6. 甲、乙、丙3家单位为希望工程共捐款176万元,所捐款数的比为2∶3∶4,问3家单位各捐款多少万元?
本题涉及的等量关系是:
耕了第二天后剩下的亩数=38亩
设这片地有x亩,根据题意得
解得 x=114.
答:这片土地一共有114亩.
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁。
——程大位《直指算法统宗》
意思是:有100个和尚分100个馒头,如果大和尚一人分3个,小和尚3人分一个,正好分完。试问大、小和尚各多少人?
9. 某人骑自行车到工厂上班,若每小时骑15km,则可早到10min;若每小时骑12km,则迟到5min.求他家到工厂的路程。
路程
12
-
路程
15
=
本题涉及的等量关系是:
10.如图,已知某长方体的展开图面积为310cm?,
求x.
本题涉及的等量关系是:
各个面的面积之和=展开图面积.
11.小丽每天要在7∶50之前赶到距家1 000m的学校上学。一天,小丽以0.8m/s的速度出发,5min后,小丽的爸爸发现她忘了带数学书.于是,爸爸立即以1.2m/s的速度去追小丽,并且在途中追上了她。
(1)爸爸追上小丽用了多长时间?
(2)追上小丽时,距离学校还有多远?
本题涉及的等量关系是:
爸爸所追路程=小丽所走路程.
12.已知y=-x?+(a-1)x+2a+3,当x=-1时,y=0.
(1)求a的值;
(2)当x=1时,求y的值.
●B组提高题
(1)将x=-1,y=0代入y=-x?+(a-1)x+2a+3,得到
关于a的一元一次方程,解之,即得a的值;
(2)将(1)求得的a的值及x=1,同时代入
y=-x?+(a-1)x+2a+3,即可求出y的值.
13.解下列方程:
不漏乘,去括号后各项的符号
14. 已知x=2是方程4(x-m)=x+2m的解,求m的值。
15. 方程2(1-x)=x-1的解与方程 的解
相同,求m的值.
先解方程2(1-x)=x-1,再将求得的x值代入方程 ,即可求出m的值.
16. 要配制含盐6%的盐水700g,已有含盐5%的盐水
200g,还需要加入含盐8%的盐水及水各多少克?
本题涉及的等量关系是:
5%盐水含盐g+8%盐水含盐g=7%盐水含盐g
本题还涉及的等量关系:
5%盐水g+8%盐水g+加水g=7%盐水g
17. 两个长方形的长与宽的比都是2∶1,大长方形的宽比小长方形的宽多3cm,大长方形的周长是小长方形的周长的2倍,求这两个长方形的面积.
【思路】求出两个长方形的长与宽,即可求两个长方形的面积.
【等量关系】大长方形周长是小长方形周长的2倍.
【解】设小长方形的宽为xcm,则长为2xcm;大长
方形的宽为(x+3)cm,长为2(x+3)cm.
根据题意得
2[(x+3)+2(x+3)]=2?2(x+2x)
解得 x=3.
所以小长方形的面积为:
3×6=18(cm?) .
大长方形的面积为:
6×9=54(cm?) .
18.要建一个长方形花圃,为了节约材料,花圃的一边靠着已建好的墙,其它三边用总长为70m的栅栏围成.现在甲、乙两人各设计了一个方案:甲的方案是长比宽多10m;乙的方案是长比宽多4m.已知墙长28m,问谁的方案比较符合实际?为什么?
本题涉及的等量关系为:
花圃的长+花圃的宽的2倍=栅栏总长70m.
“符合实际”的意思是设计的长方形花圃的长不超过墙长28m。
解:甲的方案:设花圃的宽为xm,则长为(x+10)m.
根据题意得 (x+10)+2x=70
解得 x=20.
乙的方案:设花圃的宽为ym,则长为(y+4)m.
根据题意得 (x+4)+2x=70
解得 x=22.
则长为20+10=30,而30>28,不符合实际。
则长为22+4=26,而26<28,符合实际。
综上所述,乙的方案比较符合实际。
●C组综合题
19. 足球的表面由白块和黑块组成.已知黑块是五边形,白块是六边形,且每一白块的6条边中,有三条边与黑块相接,另三边与白块相接,每一黑块的五边全与白块的边相接。已知黑块总数是12,求白块数.
从图可以看出,每个白块的三条边分别与黑块的5条边相接. 因此可得本题涉及的等量关系为
所有白块边数的一半=所有黑块的边数
解:设白块数为x,根据题意得
解得 x=20.
答:白块数为20.
20. 5名老师带领若干名学生旅游(旅游费统一支付),他们联系了标价相同的两家旅行社,经洽谈,A旅行社给的优惠条件是教师全部付费,学生按七折付费;B旅行社给的优惠条件是全体师生按八折付费.
(1)学生有多少人时,两家旅行社收费相等?
(2)现有学生20人,那么他们选哪一家旅行社费
用少些呢?
(1)题涉及的等量关系是:
A旅行社的收费=B旅行社的收费
(2)通过计算两家旅行社的收费,并比较收费多少,
确定所选旅行社。
解:(1)设标价为a元,学生有x人,根据题意得
5a+0.7ax=0.8a(x+5)
即 5+0.7x=0.8(x+5)
解得 x=10.
答:当学生是10人时,两家旅行社收费相同.
(2) 当学生是20人时,
A旅行社收费为:5a+20×0.7a=19a.
B旅行社收费为:(20+5)×0.8a=20a.
因为 a>0,
所以 19a-20a=-a<0, 即19a<20a.
所以,他们选A家旅行社费 用少些。
同课章节目录
