22.排列应用题
图片预览





文档简介
(共14张PPT)
22.排列应用题(2)
1.一条铁路原有n个车站,为适应客运需要,新增加了m个车站,客运车票增加了62种,问原有多少个车站,现有多少个车站?
2.用1 , 2 , 3三个数字, 可组成没有重复数字的自然数_________个。
3.从―9 , ―5 , 0 , 1 , 2 , 3六个数中, 每次选不重复的三个数作为直线方程ax+by+c=0的系数, 则倾斜角为钝角的直线共有___条.
例1. 6名同学并排站成一排.
(1)甲不站两端的排法有多少种
(2)甲、乙两人都不站两端的排法有多少种
(3)甲不站左端、乙不站在右端, 共有多少种排法
(4)甲必须站在乙的左边的排法有多少种?(不一定相邻)
变式1:甲、乙、丙顺序一定,有多少种站法?
变式2:6名同学站成两排,第一排站2人,第二排站4人,有多少种站法?
数学应用
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
(1)若三个女孩要站在一起,则有多少种不同的排法
捆绑法
数学应用
注:像这类有些元素必须要安排在一起(相邻)的问题,我们称之为“集团排列”问题;
解决“集团排列”问题,常用“捆绑法”,即先排集团内部的元素,再把该集团作为一个大“元素”与其他元素一起排列即可。
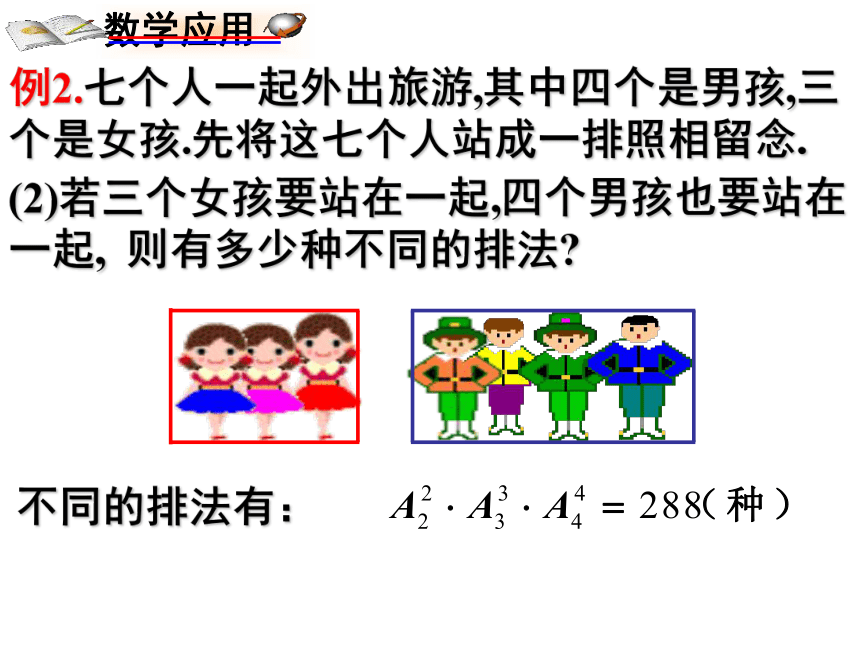
(2)若三个女孩要站在一起,四个男孩也要站在一起, 则有多少种不同的排法
不同的排法有:
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
数学应用
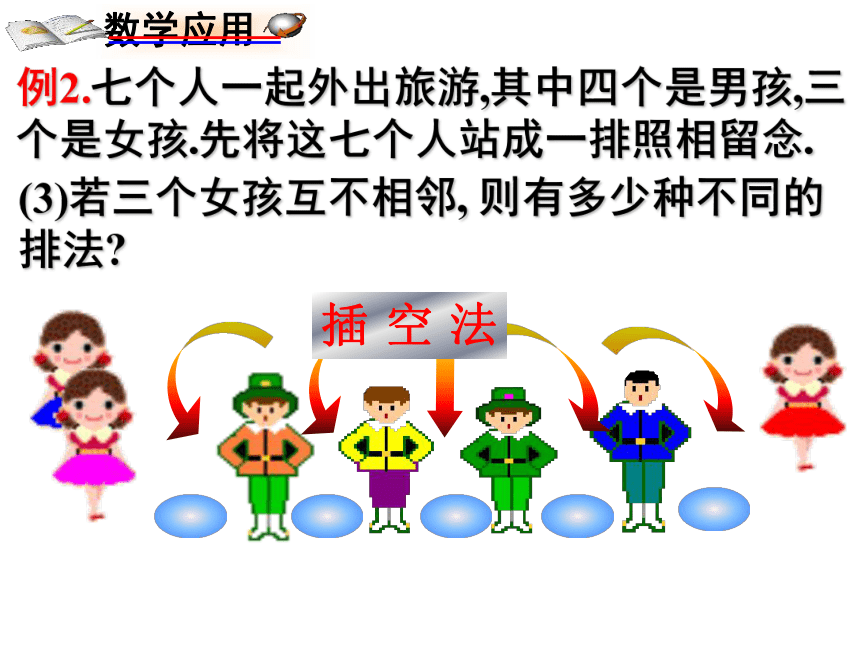
(3)若三个女孩互不相邻, 则有多少种不同的排法
插空法
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
数学应用
注:像这类有些元素不能相邻的问题,我们称之为“间隔排列”问题;
解决“间隔排列”问题,常用“插空法”,即先排不需要间隔的元素,再将需要间隔的元素用插空的方式插进来即可。
(4)若三个女孩互不相邻,四个男孩也互不相邻, 则有多少种不同的排法
不同的排法共有:
(种)
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
数学应用
1.6名同学并排站成一排,甲、乙两人必须相邻的排法有多少种?
2.(1)3男3女站成一排, 要求3女互不相邻, 共有多少种不同站法
(2)3男3女站成一排, 要求3名女生在一起, 共有多少种不同站法.
变式:
3男3女站成一排, 要求男女相间排列, 共有多少种不同站法
数学应用
例3.用1 , 2 , 3 , 4 , 5 , 6 , 7排成无重复数字的七位数, 按下列要求各有多少个这样的七位数
(1)偶数不相邻;
(2)偶数一定在奇数位上;
(3)奇数位上一定是奇数, 偶数位上一定是偶数.
某次文艺晚会上, 共演出8个节目, 其中2个唱歌、3个舞蹈、3个曲艺节目, 求分别满足下列条件的排节目单的方法种数:
(1)一个唱歌节目开头, 另一个压台;
(2)两个唱歌节目的不相邻;
(3)两个唱歌节目相邻且3个舞蹈节目不相邻.
1.带有限制的排列题,既可以从元素出发分析,也可以从位置出发分析,还可以使用去杂法.
2.对于相邻问题用“捆绑法”解决;而不相邻问题则用“插空法”.
课堂小结
作业布置:
1.订正教案20、21;
2.完成教案22。
22.排列应用题(2)
1.一条铁路原有n个车站,为适应客运需要,新增加了m个车站,客运车票增加了62种,问原有多少个车站,现有多少个车站?
2.用1 , 2 , 3三个数字, 可组成没有重复数字的自然数_________个。
3.从―9 , ―5 , 0 , 1 , 2 , 3六个数中, 每次选不重复的三个数作为直线方程ax+by+c=0的系数, 则倾斜角为钝角的直线共有___条.
例1. 6名同学并排站成一排.
(1)甲不站两端的排法有多少种
(2)甲、乙两人都不站两端的排法有多少种
(3)甲不站左端、乙不站在右端, 共有多少种排法
(4)甲必须站在乙的左边的排法有多少种?(不一定相邻)
变式1:甲、乙、丙顺序一定,有多少种站法?
变式2:6名同学站成两排,第一排站2人,第二排站4人,有多少种站法?
数学应用
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
(1)若三个女孩要站在一起,则有多少种不同的排法
捆绑法
数学应用
注:像这类有些元素必须要安排在一起(相邻)的问题,我们称之为“集团排列”问题;
解决“集团排列”问题,常用“捆绑法”,即先排集团内部的元素,再把该集团作为一个大“元素”与其他元素一起排列即可。
(2)若三个女孩要站在一起,四个男孩也要站在一起, 则有多少种不同的排法
不同的排法有:
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
数学应用
(3)若三个女孩互不相邻, 则有多少种不同的排法
插空法
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
数学应用
注:像这类有些元素不能相邻的问题,我们称之为“间隔排列”问题;
解决“间隔排列”问题,常用“插空法”,即先排不需要间隔的元素,再将需要间隔的元素用插空的方式插进来即可。
(4)若三个女孩互不相邻,四个男孩也互不相邻, 则有多少种不同的排法
不同的排法共有:
(种)
例2.七个人一起外出旅游,其中四个是男孩,三个是女孩.先将这七个人站成一排照相留念.
数学应用
1.6名同学并排站成一排,甲、乙两人必须相邻的排法有多少种?
2.(1)3男3女站成一排, 要求3女互不相邻, 共有多少种不同站法
(2)3男3女站成一排, 要求3名女生在一起, 共有多少种不同站法.
变式:
3男3女站成一排, 要求男女相间排列, 共有多少种不同站法
数学应用
例3.用1 , 2 , 3 , 4 , 5 , 6 , 7排成无重复数字的七位数, 按下列要求各有多少个这样的七位数
(1)偶数不相邻;
(2)偶数一定在奇数位上;
(3)奇数位上一定是奇数, 偶数位上一定是偶数.
某次文艺晚会上, 共演出8个节目, 其中2个唱歌、3个舞蹈、3个曲艺节目, 求分别满足下列条件的排节目单的方法种数:
(1)一个唱歌节目开头, 另一个压台;
(2)两个唱歌节目的不相邻;
(3)两个唱歌节目相邻且3个舞蹈节目不相邻.
1.带有限制的排列题,既可以从元素出发分析,也可以从位置出发分析,还可以使用去杂法.
2.对于相邻问题用“捆绑法”解决;而不相邻问题则用“插空法”.
课堂小结
作业布置:
1.订正教案20、21;
2.完成教案22。
