25.组合(3)(两课时)
图片预览








文档简介
(共30张PPT)
25.组合(3)
温故知新
组合数性质
组合数公式
例1.在100件产品中, 有98件合格品, 2件次品, 从这100件产品中任意抽出3件.
(1)一共有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件次品的抽法有多少种 (4)抽出的3件中至多有2件是正品的抽法有多少种?
数学应用
说明:“至少”“至多”的问题,通常用分类法或间接法求解。
变式
按下列条件,从12人中选出5人,有多少种不同选法?
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选.
说明:当至多(至少)中包括的情况很多时,用间接法比直接法简单的多。
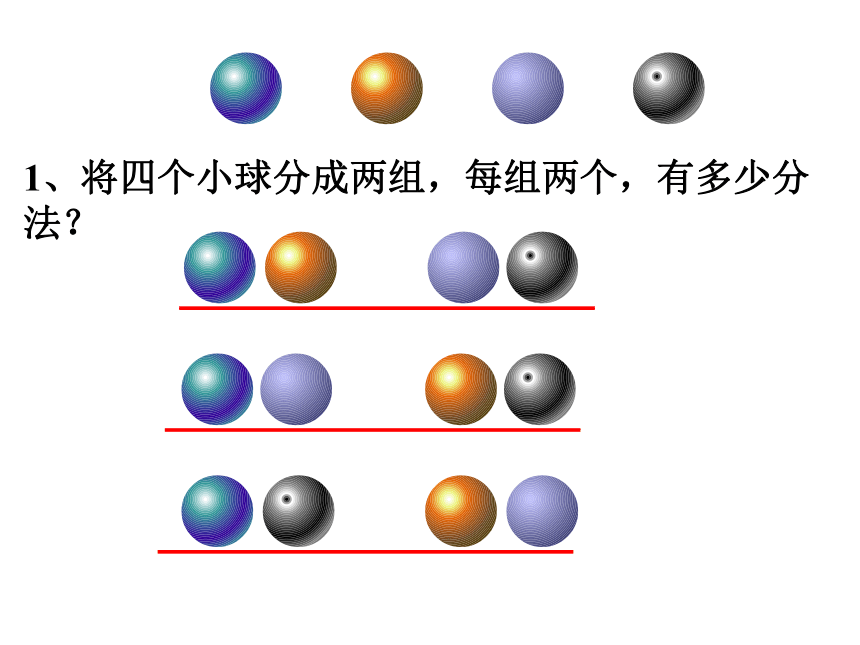
1、将四个小球分成两组,每组两个,有多少分法?
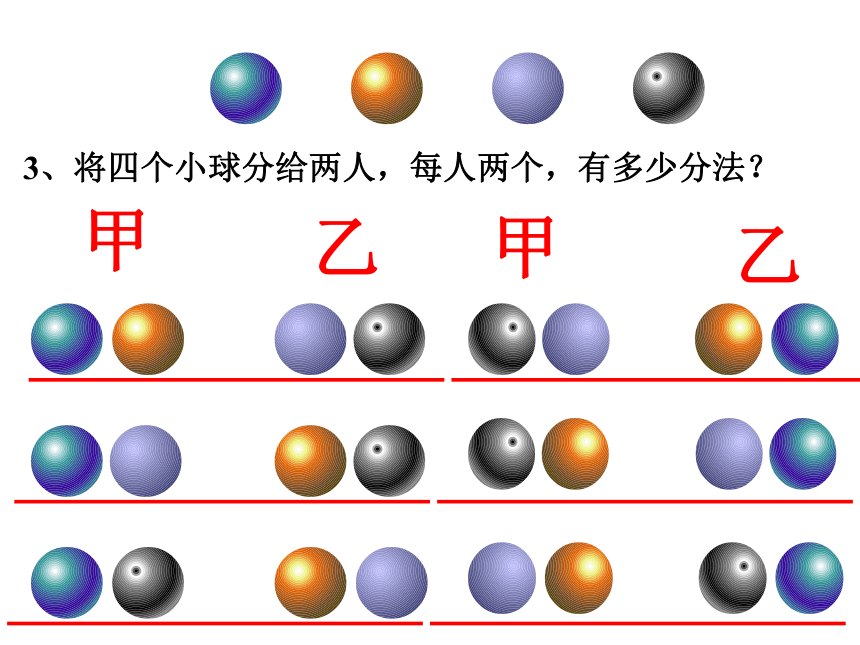
3、将四个小球分给两人,每人两个,有多少分法?
甲
甲
乙
乙
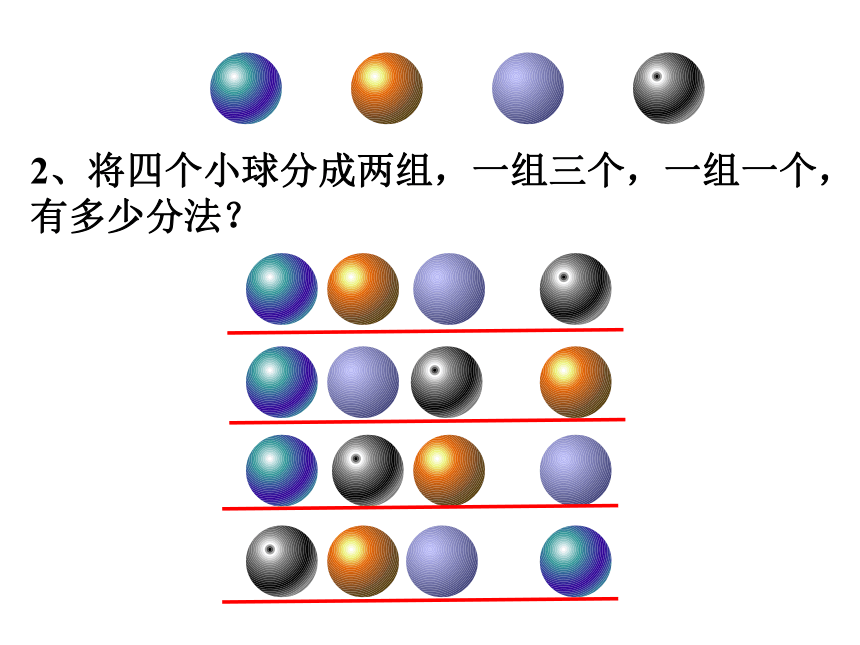
2、将四个小球分成两组,一组三个,一组一个,有多少分法?
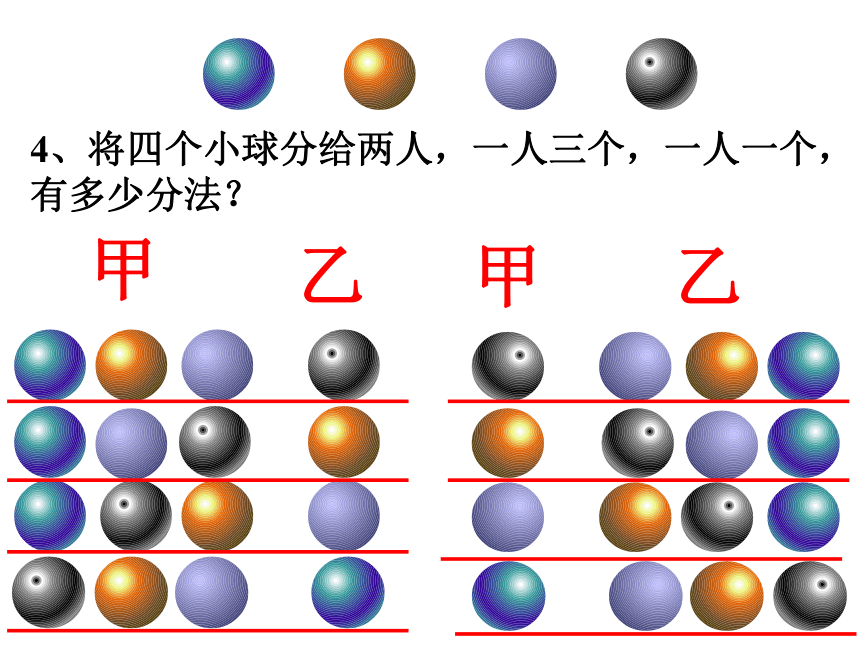
4、将四个小球分给两人,一人三个,一人一个,有多少分法?
甲
乙
甲
乙
将m·n个不同元素分成m组,每组n个元素,共有
将n个不同元素分成元素个数分别为n1, n2, … nm (ni nj ),共有
若分成的m组是有组别的,只需在原来的分组基础上再
例3.把 6本不同的书分给甲、乙、丙3人,每人2本,有多少不同的分法
变式 有6本不同的书,分成3堆. (1)如果每堆2本,有多少种分法?
(2)如果分成一堆1本,一堆2本,一堆3本,有多少种分法?
分析:这与例2不同,区别在于把 6本不同的书分给甲、乙、丙3人,每人2本,相当于把6本不同的书先分成3堆,再把分得的3堆分给甲、乙、丙3人.
练习:
1、将12个人分成2,2,2,3,3的5个组,则分组的种数是多少?
2、将5个人分成4个组,每组至少1人,则分组的种数是多少?
数学应用
例4、某旅行社有导游9人,其中3人只会英语, 2人只会日语, 其余4人既会英语又会日语,现要从中选取6人,其中3人做英语导游,3人做日语导游,则有多少种不同的选法?
练习:
有 12 名划船运动员,其中3人只会划左舷,4人只会划右舷,其余5人既会划左舷又会划右舷,现在要从这几名运动员中选出6人平均分在左、右舷划船,有多少种不同的选法?
=2174(种)
练习
导演从学校选出10名预备群众演员, 其中有2人是教师, 其余是学生, 现要选出5人上场出演, 按下列要求, 各有多少种不同的选法.
①2名教师都被选上
②教师都未被选上
③只有一名教师被选中
④至少有1名教师被选中
⑤至多有1名教师被选中
56
56
140
196
196
例5、(1)从正方体的8个顶点中取4个作为四面体的顶点可得四面体多少个
(2)在正方体的8个顶点每两点所确定的直线中,有多少对异面直线
数学应用
58
174
练习
1.平面内有12个点,其中有6点共线,此外再无3点共线,从这12个点中取3个点作三角形,一共可以作出多少个三角形 .
2.平面内有10个点,其中有某4个点在一条直线上,此外没有3点在一直线上,①可以确定多少条直线?②可以确定多少个三角形?③可以确定多少个四边形?
3.平面内有相异的11个点,有且仅有n(3≤n≤11)个点在一条直线上,过每两点作直线共有50条不同的直线,①求n,②求这11个点可确定多少个圆?
练习:
4.一个五棱柱的任意两个侧面都不平行,且底面的任意一条对角线与另一个底面的边也不平行,以它的顶点为顶点的四面体共有多少个?
或
例6 要从7个班级中选出10人来参加数学竞赛,每班至少选1人,这10个名额有多少种分配方法
例7 、从5双不同号的袜子中任取4只, 1)其中任取4只共有多少种不同的取法? 2)所取的4只中没有2只是同号的取法有多少种?(3)所取的4只中有1双是同号的取法又有多少种?(4)至少有2只袜子配成一双的取法种数是多少种?
(间接法):
例8 4个不同的小球,全部放入3个不同的盒子中,要求不能有空盒,则有多少种不同的放法?
解:方法一:从4个小球中取出2个看成一个“大球”,再行排列,共有 种.
方法二:从3个盒子中选出1个有 种选法;再从4个小球中选出2个放入盒子中,有 种方法;最后把剩下的2个小球放入剩下的2个盒子中有 种方法,故共有 种.
方法三:先将4个小球分成三组,每组分别为1个、2个、
1个小球,再放入三个盒子中有 种.
3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有多少 (98全国高考题)
解法一:首先,将3名医生分配到3所学校,每校1名,不同的分配方法有A33种;
其次,将6名护士分配到3所学校,每校2名,不同的分配方法有C62·C42·C22种;
由分步计数原理,共有A33 · C62·C42·C22 =540种
解法二:首先,给第1所学校派去1名医生和2名护士,不同的分配方法有 C31 · C62种;
其次,给第2所学校派去1名医生和2名护士,不同的分配方法有 C21 · C42种;
最后,将所剩的1名医生和2名护士派往第3所学校派去,只有1种派法.
由分步计数原理,共有C31 · C62·C21·C42 ·1=540种.
练习
1、有13个队参加篮球赛,比赛时先分成两组,第一组7个队,第二组6个队.各组都进行单循环赛(即每队都要与本组其它各队比赛一场),然后由各组的前两名共4个队进行单循环赛决出冠军、亚军,共需要比赛多少场
练习:
2、(1995年高考题)
四个不同的小球放入编号为1、2、3、4的四个盒子中,则恰有一个空盒的放法共有 种.
练习:
四、课堂小结:
①一个问题是排列问题还是组合问题,在于取出的元素之间有没有顺序,即交换其中的两个元素是否会改变所得的结果;
②组合问题解法类似于排列问题解法,并注意两个计数原理的运用,恰当选择直接法或间接法.
1、对限制条件较复杂的排列组合应用题,要周密分析,设计出合理的方案,把复杂问题分解成若干个简单的基本问题后再用两个计数原理来解决;
2、一般情况下应遵循先取元素,后排列的原则;
3、对于某些特殊问题要能熟练使用相应方法解决,如:隔板法、均匀分组(局部均匀分组)等问题.
25.组合(3)
温故知新
组合数性质
组合数公式
例1.在100件产品中, 有98件合格品, 2件次品, 从这100件产品中任意抽出3件.
(1)一共有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件次品的抽法有多少种 (4)抽出的3件中至多有2件是正品的抽法有多少种?
数学应用
说明:“至少”“至多”的问题,通常用分类法或间接法求解。
变式
按下列条件,从12人中选出5人,有多少种不同选法?
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选.
说明:当至多(至少)中包括的情况很多时,用间接法比直接法简单的多。
1、将四个小球分成两组,每组两个,有多少分法?
3、将四个小球分给两人,每人两个,有多少分法?
甲
甲
乙
乙
2、将四个小球分成两组,一组三个,一组一个,有多少分法?
4、将四个小球分给两人,一人三个,一人一个,有多少分法?
甲
乙
甲
乙
将m·n个不同元素分成m组,每组n个元素,共有
将n个不同元素分成元素个数分别为n1, n2, … nm (ni nj ),共有
若分成的m组是有组别的,只需在原来的分组基础上再
例3.把 6本不同的书分给甲、乙、丙3人,每人2本,有多少不同的分法
变式 有6本不同的书,分成3堆. (1)如果每堆2本,有多少种分法?
(2)如果分成一堆1本,一堆2本,一堆3本,有多少种分法?
分析:这与例2不同,区别在于把 6本不同的书分给甲、乙、丙3人,每人2本,相当于把6本不同的书先分成3堆,再把分得的3堆分给甲、乙、丙3人.
练习:
1、将12个人分成2,2,2,3,3的5个组,则分组的种数是多少?
2、将5个人分成4个组,每组至少1人,则分组的种数是多少?
数学应用
例4、某旅行社有导游9人,其中3人只会英语, 2人只会日语, 其余4人既会英语又会日语,现要从中选取6人,其中3人做英语导游,3人做日语导游,则有多少种不同的选法?
练习:
有 12 名划船运动员,其中3人只会划左舷,4人只会划右舷,其余5人既会划左舷又会划右舷,现在要从这几名运动员中选出6人平均分在左、右舷划船,有多少种不同的选法?
=2174(种)
练习
导演从学校选出10名预备群众演员, 其中有2人是教师, 其余是学生, 现要选出5人上场出演, 按下列要求, 各有多少种不同的选法.
①2名教师都被选上
②教师都未被选上
③只有一名教师被选中
④至少有1名教师被选中
⑤至多有1名教师被选中
56
56
140
196
196
例5、(1)从正方体的8个顶点中取4个作为四面体的顶点可得四面体多少个
(2)在正方体的8个顶点每两点所确定的直线中,有多少对异面直线
数学应用
58
174
练习
1.平面内有12个点,其中有6点共线,此外再无3点共线,从这12个点中取3个点作三角形,一共可以作出多少个三角形 .
2.平面内有10个点,其中有某4个点在一条直线上,此外没有3点在一直线上,①可以确定多少条直线?②可以确定多少个三角形?③可以确定多少个四边形?
3.平面内有相异的11个点,有且仅有n(3≤n≤11)个点在一条直线上,过每两点作直线共有50条不同的直线,①求n,②求这11个点可确定多少个圆?
练习:
4.一个五棱柱的任意两个侧面都不平行,且底面的任意一条对角线与另一个底面的边也不平行,以它的顶点为顶点的四面体共有多少个?
或
例6 要从7个班级中选出10人来参加数学竞赛,每班至少选1人,这10个名额有多少种分配方法
例7 、从5双不同号的袜子中任取4只, 1)其中任取4只共有多少种不同的取法? 2)所取的4只中没有2只是同号的取法有多少种?(3)所取的4只中有1双是同号的取法又有多少种?(4)至少有2只袜子配成一双的取法种数是多少种?
(间接法):
例8 4个不同的小球,全部放入3个不同的盒子中,要求不能有空盒,则有多少种不同的放法?
解:方法一:从4个小球中取出2个看成一个“大球”,再行排列,共有 种.
方法二:从3个盒子中选出1个有 种选法;再从4个小球中选出2个放入盒子中,有 种方法;最后把剩下的2个小球放入剩下的2个盒子中有 种方法,故共有 种.
方法三:先将4个小球分成三组,每组分别为1个、2个、
1个小球,再放入三个盒子中有 种.
3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有多少 (98全国高考题)
解法一:首先,将3名医生分配到3所学校,每校1名,不同的分配方法有A33种;
其次,将6名护士分配到3所学校,每校2名,不同的分配方法有C62·C42·C22种;
由分步计数原理,共有A33 · C62·C42·C22 =540种
解法二:首先,给第1所学校派去1名医生和2名护士,不同的分配方法有 C31 · C62种;
其次,给第2所学校派去1名医生和2名护士,不同的分配方法有 C21 · C42种;
最后,将所剩的1名医生和2名护士派往第3所学校派去,只有1种派法.
由分步计数原理,共有C31 · C62·C21·C42 ·1=540种.
练习
1、有13个队参加篮球赛,比赛时先分成两组,第一组7个队,第二组6个队.各组都进行单循环赛(即每队都要与本组其它各队比赛一场),然后由各组的前两名共4个队进行单循环赛决出冠军、亚军,共需要比赛多少场
练习:
2、(1995年高考题)
四个不同的小球放入编号为1、2、3、4的四个盒子中,则恰有一个空盒的放法共有 种.
练习:
四、课堂小结:
①一个问题是排列问题还是组合问题,在于取出的元素之间有没有顺序,即交换其中的两个元素是否会改变所得的结果;
②组合问题解法类似于排列问题解法,并注意两个计数原理的运用,恰当选择直接法或间接法.
1、对限制条件较复杂的排列组合应用题,要周密分析,设计出合理的方案,把复杂问题分解成若干个简单的基本问题后再用两个计数原理来解决;
2、一般情况下应遵循先取元素,后排列的原则;
3、对于某些特殊问题要能熟练使用相应方法解决,如:隔板法、均匀分组(局部均匀分组)等问题.
