2020-2021学年鲁教版七年级数学上册期末测试题(word解析版)
文档属性
| 名称 | 2020-2021学年鲁教版七年级数学上册期末测试题(word解析版) | 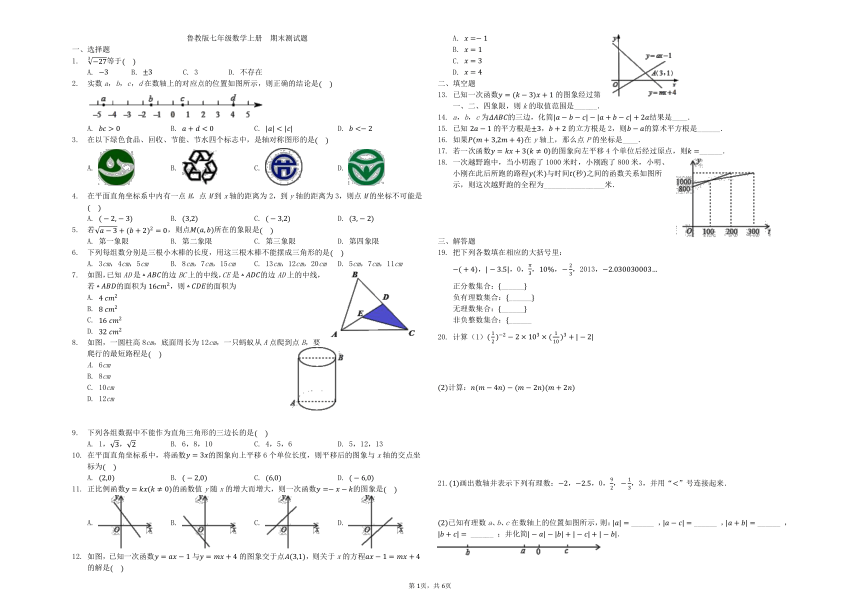 | |
| 格式 | zip | ||
| 文件大小 | 209.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 11:28:11 | ||
图片预览



文档简介
鲁教版七年级数学上册
期末测试题
一、选择题
等于
A.
B.
C.
3
D.
不存在
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是
A.
B.
C.
D.
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是
A.
B.
C.
D.
在平面直角坐标系中内有一点M,点M到x轴的距离为2,到y轴的距离为3,则点M的坐标不可能是
A.
B.
C.
D.
若,则点所在的象限是
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
下列每组数分别是三根小木棒的长度,用这三根木棒不能摆成三角形的是
A.
3cm,4cm,5cm
B.
8cm,7cm,15cm
C.
13cm,12cm,20cm
D.
5cm,7cm,11cm
如图,已知AD是的边BC上的中线,CE是的边AD上的中线,若的面积为,则的面积为
A.
B.
C.
D.
如图,一圆柱高8cm,底面周长为12cm,一只蚂蚁从A点爬到点B,要爬行的最短路程是
6cm
B.
8cm
C.
10cm
D.
12cm
下列各组数据中不能作为直角三角形的三边长的是
A.
1,,
B.
6,8,10
C.
4,5,6
D.
5,12,13
在平面直角坐标系中,将函数的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为
A.
B.
C.
D.
正比例函数的函数值y随x的增大而增大,则一次函数的图象是
A.
B.
C.
D.
如图,已知一次函数与的图象交于点,则关于x的方程的解是
A.
B.
C.
D.
二、填空题
已知一次函数的图象经过第一、二、四象限,则k的取值范围是______.
a,b,c为的三边,化简结果是____.
已知的平方根是,的立方根是2,则的算术平方根是______.
如果在y轴上,那么点P的坐标是____.
若一次函数的图象向左平移4个单位后经过原点,则______.
一次越野跑中,当小明跑了1000米时,小刚跑了800米,小明、小刚在此后所跑的路程米与时间秒之间的函数关系如图所示,则这次越野跑的全程为________________米.
三、解答题
把下列各数填在相应的大括号里:
,,0,,,,2013,
正分数集合:______
负有理数集合:______
无理数集合:______
非负整数集合:______
计算(1)
计算:
21.画出数轴并表示下列有理数:,,0,,,3,并用“”号连接起来.
已知有理数a、b、c在数轴上的位置如图所示,则:
______
,
______
,
______
,
______
;并化简.
22.如图:
画出关于x轴对称的;
在y轴上画出点P,使最小;
求的面积.
23.如图,一次函数的图象与x轴、y轴分别相交于E,F两点,点E的坐标为,,其中P是直线EF上的一个动点.
求k与b的值;
若的面积为6,求点P的坐标.
24.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,到达目的地后停止,设慢车行驶时间为x小时,两车之间的距离为y千米,两者的关系如图所示,根据图象探究:
看图填空:两车出发小时,两车相遇;
求快车和慢车的速度;
求线段BC所表示的y与x的关系式,并求两车行驶6小时两车相距多少千米.
答案和解析
1.【答案】A
【解析】解:,
故选:A.
根据立方根的定义求出即可.
本题考查了立方根的定义和立方根的性质,能知道a的立方根是是解此题的关键,注意:一个正数有一个正的立方根,0的立方根是0,一个负数有一个负的立方根.
2.【答案】B
【解析】
【试题解析】
【分析】
本题考查了实数与数轴以及绝对值,观察数轴,逐一分析四个选项的正误是解题的关键.
观察数轴,找出a、b、c、d四个数的大概范围,再逐一分析四个选项的正误,即可得出结论.
【解答】
解:A、,,
,结论A错误;
B、,,
,结论B正确;
C、,,
,结论C错误;
D、,结论D错误.
故选:B.
3.【答案】D
【解析】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选:D.
根据轴对称图形的概念对各选项分析判断利用排除法求解.
本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
4.【答案】A
【解析】解:到x轴的距离为2,到y轴的距离为3,
的纵坐标可能为,横坐标可能为,
的坐标为或或或.
故选:A.
先根据到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值,得到具体坐标即可求解.
本题考查点的坐标的确定,用到的知识点为:点到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值.
5.【答案】D
【解析】解:,
,,
解得:,,
点所在的象限是:第四象限.
故选:D.
直接利用偶次方的性质以及算术平方根的性质得出a,b的值,进而判断出点M所在的象限.
此题主要考查了偶次方的性质以及算术平方根的性质及点所在的象限,正确得出a,b的值是解题关键.
6.【答案】B
【解析】解:A、,故以这三条线段可以构成三角形,选项错误;
B、,故以这三条线段不能构成三角形,选项正确.
C、,故以这三条线段能构成三角形,选项错误;
D、,故以这三条线段能构成三角形,选项错误;
故选:B.
根据三角形的三边关系,两边之和大于第三边,即两短边的和大于最长的边,即可作出判断.
本题主要考查了三角形的三边关系,正确理解定理是解题关键.
7.【答案】B
【解析】
【分析】
本题主要考查了三角形面积的求法和三角形的中线,掌握三角形的中线将三角形分成面积相等的两部分是解答本题的关键.根据三角形的中线把三角形分成面积相等的两部即可求出的面积.
【解答】
解:是边BC上的中线,
,
是中AD边上的中线,
,
,
故选B.
8.【答案】C
【解析】解:底面周长为12cm,半圆弧长为6cm,
展开得:
又因为,,
根据勾股定理得:.
故选:C.
此题最直接的解法,就是将圆柱展开,然后利用两点之间线段最短解答.
此题主要考查了平面展开最短路径问题,解题的关键是根据题意画出展开图,表示出各线段的长度.
9.【答案】C
【解析】解:A、,故是直角三角形;
B、,故是直角三角形;
C、,故不是直角三角形;
D、,故是直角三角形.
故选:C.
由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
10.【答案】B
【解析】解:由“上加下减”的原则可知,将函数的图象向上平移6个单位长度所得函数的解析式为,
此时与x轴相交,则,
,即,
点的坐标为,
故选:B.
根据“上加下减”的原则求得平移后的解析式,令,解得即可.
本题考查的是一次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.
11.【答案】B
【解析】解:正比例函数是常数,的函数值y随x的增大而增大,
,
一次函数,
,,
此函数的图象经过二三四象限.
故选:B.
先根据正比例函数是常数,的函数值y随x的增大而增大判断出k的符号,再根据一次函数的图象与系数的关系即可得出结论.
本题考查的是一次函数的图象与系数的关系,熟知一次函数中,当,时函数的图象在一、二、四象限是解答此题的关键.
12.【答案】C
【解析】解:一次函数与的图象交于点,
的解是.
故选:C.
根据方程的解即为函数图象的交点坐标解答.
本题主要考查了一次函数与一元一次方程.函数图象交点坐标为两函数解析式组成的方程的解.
13.【答案】
【解析】
【分析】
本题考查一次函数图象与系数的关系;熟练掌握一次函数,k与b对函数图象的影响是解题的关键.
根据,,时,函数图象经过第一、二、四象限,则有即可求解.
【解答】
解:的图象经过第一、二、四象限,
,
;
故答案为;
14.【答案】2c
【解析】
【分析】
本题考查了三角形三边的关系及绝对值符号的消除问题,解题的关键是了解负数的绝对值是其相反数,难度不大。根据三角形三边的关系得到,,则根据二次根式的性质得原式,然后去括号后合并即可。
【解答】
解:,b,c为的三边,
,,
原式
。
故答案为:2c。
15.【答案】1
【解析】解:的平方根是,的立方根是2,
,,
,,
,
的算术平方根是1;
故答案为:1.
根据的平方根是,的立方根是2,得出,,求出,,求出的值,从而得出的算术平方根.
本题考查平方根、立方根与算术平方根;熟练掌握平方根、立方根、算术平方根的定义是解题的关键.
16.【答案】
【解析】
【分析】
本题考查了点的坐标,利用y轴上点的横坐标等于零得出是解题关键.根据各象限内点的坐标特征解答即可.
【解答】
解:由题意,得
,
解得,
,
即,
故答案为.
?
17.【答案】
【解析】解:一次函数的图象向左平移4个单位后得到;
经过原点,
,
解得,
故答案为.
根据平移的规律得新抛物线的解析式,把代入即可.
本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,熟练掌握平移的规律是解题的关键.
18.【答案】1600
【解析】
【分析】
本题考查了行程问题的数量关系的运用,二元一次方程组的解法的运用,解答时由函数图象的数量关系建立方程组是关键.
设小明的速度为a米秒,小刚的速度为b米秒,由行程问题的数量关系建立方程组求出其解即可.
【解答】
解:设小明的速度为a米秒,小刚的速度为b米秒,由题意,得
解得:
这次越野跑的全程为:米.
故答案为:1600.
19.【答案】,?
,?,?
0,
【解析】解:是负整数,是正分数,0是整数,不是正数也不是负数,
不是有理数,是分数,是分数,2013是整数,不是有理数.
正分数集合
负有理数集合
无理数集合
非负整数集合
故答案为:,,,.
先对,化简,再根据各个集合的要求去选择.
本题考查了实数的分类,掌握实数的相关概念是关键.注意虽然具有分数的形式,却是无理数.
20.【答案】解:解:原式;
解:原式.
【解析】根据有理数的混合运算顺序计算即可;
根据单项式乘多项式以及平方差公式计算即可.
本题主要考查了有理数的混合运算以及整数的混合运算,熟练掌握运算法则是解答本题的关键.
21.【答案】?
?
?
【解析】解:,
?;
,,,,
由数轴可知:,
,
故答案为:、、、.
先在数轴上表示出各个数,再比较即可;
先关键绝对值的性质去掉绝对值符号,再算加减即可.
本题考查了整式的加减,数轴,绝对值,相反数,实数的大小比较等知识点,能正确在数轴上表示出各个数是解的关键,能正确去掉绝对值符号是解的关键.
22.【答案】解:
如图所示,即为所求;
如图所示,点P即为所求;
如图所示,
.
【解析】
【分析】
本题考查轴对称变换、三角形的面积、两点之间线段最短等知识,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.
分别作出点A、B、C关于x轴对称的点,,,然后顺次连接,并写出坐标.
作点A关于y轴的对称点连接交y轴于点P,则最小,点P即为所求.
利用所在梯形面积减去周围三角形面积,进而得出答案.
23.【答案】解:,
,
,
把E的坐标为代入直线得,,
解得:,
如图,
设,
,
,即或,
是直线EF上的一个动点,
当时,即,解得:,
,
当时,即,解得:,
,
综上,点P的坐标为或.
【解析】本题考查的是一次函数图象点的坐标特征,待定系数法求一次函数解析式,三角形的面积有关知识.
先根据确定出点F的坐标,进而求出b,再将点E的坐标代入即可求出k的值;
确定直线的关系式,若的面积为6,以为底,因此高为2,即点P的纵坐标为2或,然后代入直线的关系式求出点P的坐标.
24.【答案】解:由图知:两车出发小时相遇;
快车8小时到达,慢车12小时到达,
故:快车速度为千米时,
慢车速度为千米时;
由题可得,点C是快车刚到达乙地,
点C的横坐标是8,
纵坐标是:,
即点C的坐标为.
设线段BC对应的函数解析式为,
点,点,
,解得,
线段BC所表示的y与x的函数关系式是.
当时,,
即两车行驶6小时两车相距300千米.
【解析】根据图象可知两车出发小时相遇;
根据图象和题意可以分别求出慢车和快车的速度;
根据题意可以求得点C的坐标,由图象可以得到点B的坐标,从而可以得到线段BC所表示的y与x之间的函数关系式,再把代入求出对应的y值即可得出两车行驶6小时两车相距多少千米.
本题考查一次函数的应用,路程、速度与时间关系的应用,待定系数法求一次函数的解析式以及求函数值,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
第1页,共6页
期末测试题
一、选择题
等于
A.
B.
C.
3
D.
不存在
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是
A.
B.
C.
D.
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是
A.
B.
C.
D.
在平面直角坐标系中内有一点M,点M到x轴的距离为2,到y轴的距离为3,则点M的坐标不可能是
A.
B.
C.
D.
若,则点所在的象限是
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
下列每组数分别是三根小木棒的长度,用这三根木棒不能摆成三角形的是
A.
3cm,4cm,5cm
B.
8cm,7cm,15cm
C.
13cm,12cm,20cm
D.
5cm,7cm,11cm
如图,已知AD是的边BC上的中线,CE是的边AD上的中线,若的面积为,则的面积为
A.
B.
C.
D.
如图,一圆柱高8cm,底面周长为12cm,一只蚂蚁从A点爬到点B,要爬行的最短路程是
6cm
B.
8cm
C.
10cm
D.
12cm
下列各组数据中不能作为直角三角形的三边长的是
A.
1,,
B.
6,8,10
C.
4,5,6
D.
5,12,13
在平面直角坐标系中,将函数的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为
A.
B.
C.
D.
正比例函数的函数值y随x的增大而增大,则一次函数的图象是
A.
B.
C.
D.
如图,已知一次函数与的图象交于点,则关于x的方程的解是
A.
B.
C.
D.
二、填空题
已知一次函数的图象经过第一、二、四象限,则k的取值范围是______.
a,b,c为的三边,化简结果是____.
已知的平方根是,的立方根是2,则的算术平方根是______.
如果在y轴上,那么点P的坐标是____.
若一次函数的图象向左平移4个单位后经过原点,则______.
一次越野跑中,当小明跑了1000米时,小刚跑了800米,小明、小刚在此后所跑的路程米与时间秒之间的函数关系如图所示,则这次越野跑的全程为________________米.
三、解答题
把下列各数填在相应的大括号里:
,,0,,,,2013,
正分数集合:______
负有理数集合:______
无理数集合:______
非负整数集合:______
计算(1)
计算:
21.画出数轴并表示下列有理数:,,0,,,3,并用“”号连接起来.
已知有理数a、b、c在数轴上的位置如图所示,则:
______
,
______
,
______
,
______
;并化简.
22.如图:
画出关于x轴对称的;
在y轴上画出点P,使最小;
求的面积.
23.如图,一次函数的图象与x轴、y轴分别相交于E,F两点,点E的坐标为,,其中P是直线EF上的一个动点.
求k与b的值;
若的面积为6,求点P的坐标.
24.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,到达目的地后停止,设慢车行驶时间为x小时,两车之间的距离为y千米,两者的关系如图所示,根据图象探究:
看图填空:两车出发小时,两车相遇;
求快车和慢车的速度;
求线段BC所表示的y与x的关系式,并求两车行驶6小时两车相距多少千米.
答案和解析
1.【答案】A
【解析】解:,
故选:A.
根据立方根的定义求出即可.
本题考查了立方根的定义和立方根的性质,能知道a的立方根是是解此题的关键,注意:一个正数有一个正的立方根,0的立方根是0,一个负数有一个负的立方根.
2.【答案】B
【解析】
【试题解析】
【分析】
本题考查了实数与数轴以及绝对值,观察数轴,逐一分析四个选项的正误是解题的关键.
观察数轴,找出a、b、c、d四个数的大概范围,再逐一分析四个选项的正误,即可得出结论.
【解答】
解:A、,,
,结论A错误;
B、,,
,结论B正确;
C、,,
,结论C错误;
D、,结论D错误.
故选:B.
3.【答案】D
【解析】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选:D.
根据轴对称图形的概念对各选项分析判断利用排除法求解.
本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
4.【答案】A
【解析】解:到x轴的距离为2,到y轴的距离为3,
的纵坐标可能为,横坐标可能为,
的坐标为或或或.
故选:A.
先根据到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值,得到具体坐标即可求解.
本题考查点的坐标的确定,用到的知识点为:点到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值.
5.【答案】D
【解析】解:,
,,
解得:,,
点所在的象限是:第四象限.
故选:D.
直接利用偶次方的性质以及算术平方根的性质得出a,b的值,进而判断出点M所在的象限.
此题主要考查了偶次方的性质以及算术平方根的性质及点所在的象限,正确得出a,b的值是解题关键.
6.【答案】B
【解析】解:A、,故以这三条线段可以构成三角形,选项错误;
B、,故以这三条线段不能构成三角形,选项正确.
C、,故以这三条线段能构成三角形,选项错误;
D、,故以这三条线段能构成三角形,选项错误;
故选:B.
根据三角形的三边关系,两边之和大于第三边,即两短边的和大于最长的边,即可作出判断.
本题主要考查了三角形的三边关系,正确理解定理是解题关键.
7.【答案】B
【解析】
【分析】
本题主要考查了三角形面积的求法和三角形的中线,掌握三角形的中线将三角形分成面积相等的两部分是解答本题的关键.根据三角形的中线把三角形分成面积相等的两部即可求出的面积.
【解答】
解:是边BC上的中线,
,
是中AD边上的中线,
,
,
故选B.
8.【答案】C
【解析】解:底面周长为12cm,半圆弧长为6cm,
展开得:
又因为,,
根据勾股定理得:.
故选:C.
此题最直接的解法,就是将圆柱展开,然后利用两点之间线段最短解答.
此题主要考查了平面展开最短路径问题,解题的关键是根据题意画出展开图,表示出各线段的长度.
9.【答案】C
【解析】解:A、,故是直角三角形;
B、,故是直角三角形;
C、,故不是直角三角形;
D、,故是直角三角形.
故选:C.
由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
10.【答案】B
【解析】解:由“上加下减”的原则可知,将函数的图象向上平移6个单位长度所得函数的解析式为,
此时与x轴相交,则,
,即,
点的坐标为,
故选:B.
根据“上加下减”的原则求得平移后的解析式,令,解得即可.
本题考查的是一次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.
11.【答案】B
【解析】解:正比例函数是常数,的函数值y随x的增大而增大,
,
一次函数,
,,
此函数的图象经过二三四象限.
故选:B.
先根据正比例函数是常数,的函数值y随x的增大而增大判断出k的符号,再根据一次函数的图象与系数的关系即可得出结论.
本题考查的是一次函数的图象与系数的关系,熟知一次函数中,当,时函数的图象在一、二、四象限是解答此题的关键.
12.【答案】C
【解析】解:一次函数与的图象交于点,
的解是.
故选:C.
根据方程的解即为函数图象的交点坐标解答.
本题主要考查了一次函数与一元一次方程.函数图象交点坐标为两函数解析式组成的方程的解.
13.【答案】
【解析】
【分析】
本题考查一次函数图象与系数的关系;熟练掌握一次函数,k与b对函数图象的影响是解题的关键.
根据,,时,函数图象经过第一、二、四象限,则有即可求解.
【解答】
解:的图象经过第一、二、四象限,
,
;
故答案为;
14.【答案】2c
【解析】
【分析】
本题考查了三角形三边的关系及绝对值符号的消除问题,解题的关键是了解负数的绝对值是其相反数,难度不大。根据三角形三边的关系得到,,则根据二次根式的性质得原式,然后去括号后合并即可。
【解答】
解:,b,c为的三边,
,,
原式
。
故答案为:2c。
15.【答案】1
【解析】解:的平方根是,的立方根是2,
,,
,,
,
的算术平方根是1;
故答案为:1.
根据的平方根是,的立方根是2,得出,,求出,,求出的值,从而得出的算术平方根.
本题考查平方根、立方根与算术平方根;熟练掌握平方根、立方根、算术平方根的定义是解题的关键.
16.【答案】
【解析】
【分析】
本题考查了点的坐标,利用y轴上点的横坐标等于零得出是解题关键.根据各象限内点的坐标特征解答即可.
【解答】
解:由题意,得
,
解得,
,
即,
故答案为.
?
17.【答案】
【解析】解:一次函数的图象向左平移4个单位后得到;
经过原点,
,
解得,
故答案为.
根据平移的规律得新抛物线的解析式,把代入即可.
本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,熟练掌握平移的规律是解题的关键.
18.【答案】1600
【解析】
【分析】
本题考查了行程问题的数量关系的运用,二元一次方程组的解法的运用,解答时由函数图象的数量关系建立方程组是关键.
设小明的速度为a米秒,小刚的速度为b米秒,由行程问题的数量关系建立方程组求出其解即可.
【解答】
解:设小明的速度为a米秒,小刚的速度为b米秒,由题意,得
解得:
这次越野跑的全程为:米.
故答案为:1600.
19.【答案】,?
,?,?
0,
【解析】解:是负整数,是正分数,0是整数,不是正数也不是负数,
不是有理数,是分数,是分数,2013是整数,不是有理数.
正分数集合
负有理数集合
无理数集合
非负整数集合
故答案为:,,,.
先对,化简,再根据各个集合的要求去选择.
本题考查了实数的分类,掌握实数的相关概念是关键.注意虽然具有分数的形式,却是无理数.
20.【答案】解:解:原式;
解:原式.
【解析】根据有理数的混合运算顺序计算即可;
根据单项式乘多项式以及平方差公式计算即可.
本题主要考查了有理数的混合运算以及整数的混合运算,熟练掌握运算法则是解答本题的关键.
21.【答案】?
?
?
【解析】解:,
?;
,,,,
由数轴可知:,
,
故答案为:、、、.
先在数轴上表示出各个数,再比较即可;
先关键绝对值的性质去掉绝对值符号,再算加减即可.
本题考查了整式的加减,数轴,绝对值,相反数,实数的大小比较等知识点,能正确在数轴上表示出各个数是解的关键,能正确去掉绝对值符号是解的关键.
22.【答案】解:
如图所示,即为所求;
如图所示,点P即为所求;
如图所示,
.
【解析】
【分析】
本题考查轴对称变换、三角形的面积、两点之间线段最短等知识,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.
分别作出点A、B、C关于x轴对称的点,,,然后顺次连接,并写出坐标.
作点A关于y轴的对称点连接交y轴于点P,则最小,点P即为所求.
利用所在梯形面积减去周围三角形面积,进而得出答案.
23.【答案】解:,
,
,
把E的坐标为代入直线得,,
解得:,
如图,
设,
,
,即或,
是直线EF上的一个动点,
当时,即,解得:,
,
当时,即,解得:,
,
综上,点P的坐标为或.
【解析】本题考查的是一次函数图象点的坐标特征,待定系数法求一次函数解析式,三角形的面积有关知识.
先根据确定出点F的坐标,进而求出b,再将点E的坐标代入即可求出k的值;
确定直线的关系式,若的面积为6,以为底,因此高为2,即点P的纵坐标为2或,然后代入直线的关系式求出点P的坐标.
24.【答案】解:由图知:两车出发小时相遇;
快车8小时到达,慢车12小时到达,
故:快车速度为千米时,
慢车速度为千米时;
由题可得,点C是快车刚到达乙地,
点C的横坐标是8,
纵坐标是:,
即点C的坐标为.
设线段BC对应的函数解析式为,
点,点,
,解得,
线段BC所表示的y与x的函数关系式是.
当时,,
即两车行驶6小时两车相距300千米.
【解析】根据图象可知两车出发小时相遇;
根据图象和题意可以分别求出慢车和快车的速度;
根据题意可以求得点C的坐标,由图象可以得到点B的坐标,从而可以得到线段BC所表示的y与x之间的函数关系式,再把代入求出对应的y值即可得出两车行驶6小时两车相距多少千米.
本题考查一次函数的应用,路程、速度与时间关系的应用,待定系数法求一次函数的解析式以及求函数值,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
第1页,共6页
同课章节目录
