华师大版八下数学 18.1.1平行四边形边、角的性质 教案
文档属性
| 名称 | 华师大版八下数学 18.1.1平行四边形边、角的性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览

文档简介
§18.1 平行四边形的性质
教学目标
知识与技能:探索并掌握平行四边形对边相等、对角相等等有关性质,理解其内涵.
过程与方法:经历探索平行四边形的有关概念和性质的过程,发展学生的合作意识以及识图能力.
情感态度与价值观:观察学生合情推理能力和良好的逻辑思维,提高学生的几何语言表示能力.
重点、难点
重点:平行四边形的概念和特征.
难点:探索和掌握平行四边形的特征.
教具
多媒体 几何画板
教学过程
一、创设情景,导入新知
1、出示投影 课本P71章前图与文.
2、多媒体课件展示图片,通过观察图案,指出平行四边形是我们生活中常见的一种图形.
3、让学生交流生活中见到的平行四边形.
二、合作探索,展示交流
1、概念引入:两组对边分别平行的四边形叫做平行四边形.
记作 □ABCD 读作:平行四边形ABCD
判定:∵AB∥CD, AD∥BC
∴四边形ABCD是平行四边形。
性质: ∵四边形ABCD是平行四边形 (在□ABCD中)
∴AB∥CD ,AD∥BC
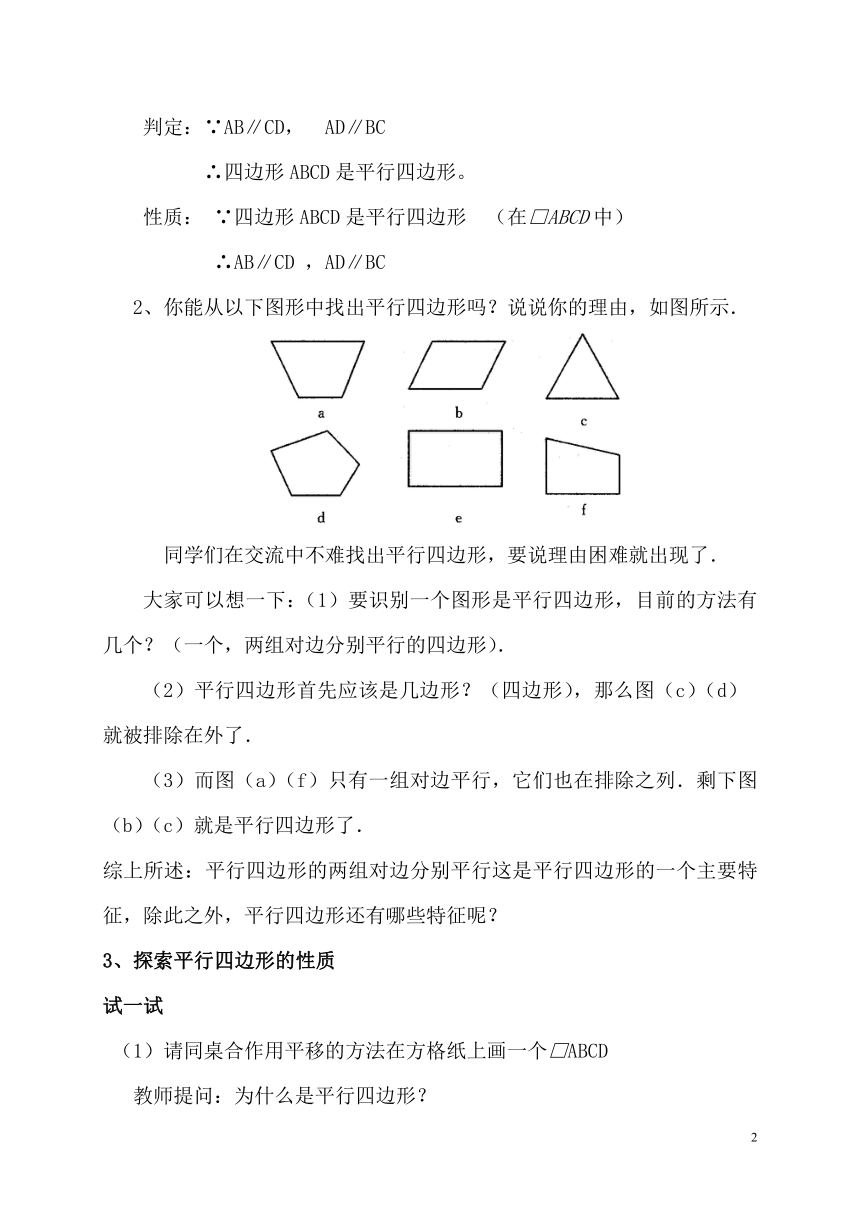
2、你能从以下图形中找出平行四边形吗?说说你的理由,如图所示.
同学们在交流中不难找出平行四边形,要说理由困难就出现了.
大家可以想一下:(1)要识别一个图形是平行四边形,目前的方法有几个?(一个,两组对边分别平行的四边形).
(2)平行四边形首先应该是几边形?(四边形),那么图(c)(d)就被排除在外了.
(3)而图(a)(f)只有一组对边平行,它们也在排除之列.剩下图(b)(c)就是平行四边形了.
综上所述:平行四边形的两组对边分别平行这是平行四边形的一个主要特征,除此之外,平行四边形还有哪些特征呢?
3、探索平行四边形的性质
试一试
(1)请同桌合作用平移的方法在方格纸上画一个□ABCD
教师提问:为什么是平行四边形?
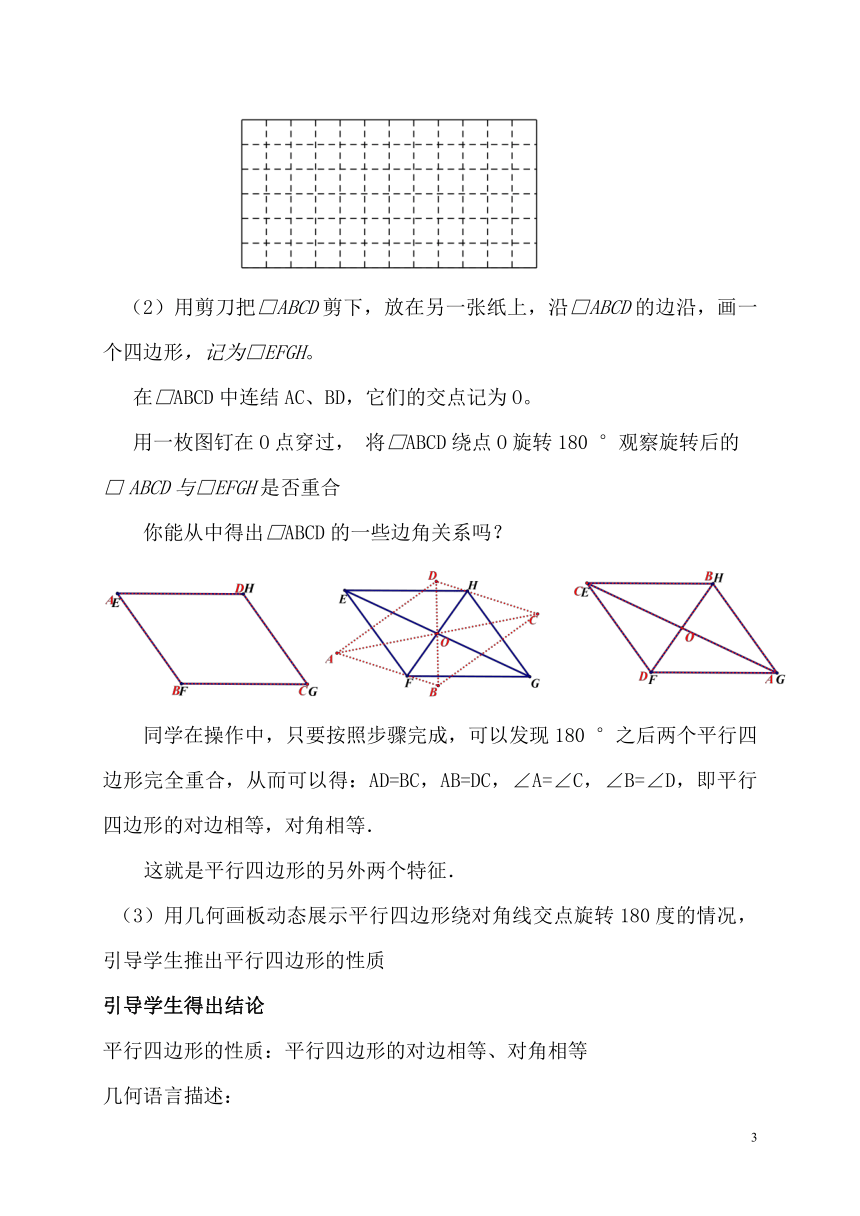
(2)用剪刀把□ABCD剪下,放在另一张纸上,沿□ABCD的边沿,画一个四边形,记为□EFGH。
在□ABCD中连结AC、BD,它们的交点记为O。
用一枚图钉在O点穿过, 将□ABCD绕点O旋转180°观察旋转后的
ABCD与□EFGH是否重合
你能从中得出□ABCD的一些边角关系吗?
同学在操作中,只要按照步骤完成,可以发现180°之后两个平行四边形完全重合,从而可以得:AD=BC,AB=DC,∠A=∠C,∠B=∠D,即平行四边形的对边相等,对角相等.
这就是平行四边形的另外两个特征.
(3)用几何画板动态展示平行四边形绕对角线交点旋转180度的情况,引导学生推出平行四边形的性质
引导学生得出结论
平行四边形的性质:平行四边形的对边相等、对角相等
几何语言描述:
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
或 在 □ABCD中,
∠D= ∠B, ∠C= ∠A .(平行四边形的对角相等)
4、例题讲解
例1.已知:□ABCD中,∠A=40°,你能求出其他各角的度数吗?说说你的理由.
解:在 □ABCD中,∠A=40°
∠D=∠B,∠C=∠A=40°(平行四边形的对角相等)
又∵AD∥BC
∴∠B= 180 °-∠A= 180 °- 40°=140°
∴∠D= ∠B=140°
变式1.已知:□ABCD中,若∠1=80°,你能求出各角的度数吗?说说你的理由
变式2.已知:□ABCD中, 若∠A+∠C=80°,你能求出各角的度数吗?说说你的理由.
例2.如图:□ABCD,AB=8, 你能求哪条边?
解:在 □ABCD中,
AB=DC(平行四边形的对边相等)
又∵AB=8
∴CD=8
变式1,如图:已知□ABCD,AB=8,BC=5, 你还能求哪条边?
变式2.如图:已知□ABCD,AB=8,周长等于24,求其余三条边的长.
解:在 □ABCD中,AB=DC,AD=BC(平行四边形的对边相等)
又∵AB=8,AB+BC+CD+DA=24
∴CD=8,AD=BC=4
5、平行线之间的距离
(1)明确平行线间的距离概念
(2) 动手实践平行线间的距离的关系
概括:平行线之间的距离处处相等
6、巩固提高
如图所示,四边形ABCD是平行四边形
①若∠A=120° ,则∠B= ;∠C= ;∠D= 。
②若AB+BC=13,求它的周长。
7、小结回顾
① 平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
② 平行四边形的性质:
边 对边平行且相等
角 对角相等 邻角互补
8、作业布置
课本习题18.1第1、3题
9、板书设计
6
教学目标
知识与技能:探索并掌握平行四边形对边相等、对角相等等有关性质,理解其内涵.
过程与方法:经历探索平行四边形的有关概念和性质的过程,发展学生的合作意识以及识图能力.
情感态度与价值观:观察学生合情推理能力和良好的逻辑思维,提高学生的几何语言表示能力.
重点、难点
重点:平行四边形的概念和特征.
难点:探索和掌握平行四边形的特征.
教具
多媒体 几何画板
教学过程
一、创设情景,导入新知
1、出示投影 课本P71章前图与文.
2、多媒体课件展示图片,通过观察图案,指出平行四边形是我们生活中常见的一种图形.
3、让学生交流生活中见到的平行四边形.
二、合作探索,展示交流
1、概念引入:两组对边分别平行的四边形叫做平行四边形.
记作 □ABCD 读作:平行四边形ABCD
判定:∵AB∥CD, AD∥BC
∴四边形ABCD是平行四边形。
性质: ∵四边形ABCD是平行四边形 (在□ABCD中)
∴AB∥CD ,AD∥BC
2、你能从以下图形中找出平行四边形吗?说说你的理由,如图所示.
同学们在交流中不难找出平行四边形,要说理由困难就出现了.
大家可以想一下:(1)要识别一个图形是平行四边形,目前的方法有几个?(一个,两组对边分别平行的四边形).
(2)平行四边形首先应该是几边形?(四边形),那么图(c)(d)就被排除在外了.
(3)而图(a)(f)只有一组对边平行,它们也在排除之列.剩下图(b)(c)就是平行四边形了.
综上所述:平行四边形的两组对边分别平行这是平行四边形的一个主要特征,除此之外,平行四边形还有哪些特征呢?
3、探索平行四边形的性质
试一试
(1)请同桌合作用平移的方法在方格纸上画一个□ABCD
教师提问:为什么是平行四边形?
(2)用剪刀把□ABCD剪下,放在另一张纸上,沿□ABCD的边沿,画一个四边形,记为□EFGH。
在□ABCD中连结AC、BD,它们的交点记为O。
用一枚图钉在O点穿过, 将□ABCD绕点O旋转180°观察旋转后的
ABCD与□EFGH是否重合
你能从中得出□ABCD的一些边角关系吗?
同学在操作中,只要按照步骤完成,可以发现180°之后两个平行四边形完全重合,从而可以得:AD=BC,AB=DC,∠A=∠C,∠B=∠D,即平行四边形的对边相等,对角相等.
这就是平行四边形的另外两个特征.
(3)用几何画板动态展示平行四边形绕对角线交点旋转180度的情况,引导学生推出平行四边形的性质
引导学生得出结论
平行四边形的性质:平行四边形的对边相等、对角相等
几何语言描述:
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
或 在 □ABCD中,
∠D= ∠B, ∠C= ∠A .(平行四边形的对角相等)
4、例题讲解
例1.已知:□ABCD中,∠A=40°,你能求出其他各角的度数吗?说说你的理由.
解:在 □ABCD中,∠A=40°
∠D=∠B,∠C=∠A=40°(平行四边形的对角相等)
又∵AD∥BC
∴∠B= 180 °-∠A= 180 °- 40°=140°
∴∠D= ∠B=140°
变式1.已知:□ABCD中,若∠1=80°,你能求出各角的度数吗?说说你的理由
变式2.已知:□ABCD中, 若∠A+∠C=80°,你能求出各角的度数吗?说说你的理由.
例2.如图:□ABCD,AB=8, 你能求哪条边?
解:在 □ABCD中,
AB=DC(平行四边形的对边相等)
又∵AB=8
∴CD=8
变式1,如图:已知□ABCD,AB=8,BC=5, 你还能求哪条边?
变式2.如图:已知□ABCD,AB=8,周长等于24,求其余三条边的长.
解:在 □ABCD中,AB=DC,AD=BC(平行四边形的对边相等)
又∵AB=8,AB+BC+CD+DA=24
∴CD=8,AD=BC=4
5、平行线之间的距离
(1)明确平行线间的距离概念
(2) 动手实践平行线间的距离的关系
概括:平行线之间的距离处处相等
6、巩固提高
如图所示,四边形ABCD是平行四边形
①若∠A=120° ,则∠B= ;∠C= ;∠D= 。
②若AB+BC=13,求它的周长。
7、小结回顾
① 平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
② 平行四边形的性质:
边 对边平行且相等
角 对角相等 邻角互补
8、作业布置
课本习题18.1第1、3题
9、板书设计
6
