五年级下册数学教案因数与倍数(人教版)表格版
文档属性
| 名称 | 五年级下册数学教案因数与倍数(人教版)表格版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 19:30:26 | ||
图片预览

文档简介
(五)年级(数学)学科备课
教师
授课时间
(
)月(
)日
课时
第(
)课时
课题
最小公倍数例3
课型
新授
学习目标
1、能运用公倍数和最小公倍数的知识解决简单的实际问题。
2、通过学生动手摆一摆理解题意,并找出解决问题的方法。
3、通过将实际问题转化成数学问题,培养学生分析问题和解决问题的能力。
重点
结合具体的现实情境,体会公倍数和最小公倍数的应用。
难点
找出解决问题的方法。
教学具准备
PPT、长方形、学习卡
主备课人
教
学
过
程
一、复习引入(2分钟)
1、求出下列各数的最小公倍数。
5和7的最小公倍数(
)
12和36的最小公倍数是
(
)
4和6的最小公倍数是
(
)
2、导入新课
同学们最小公倍数跟我们的生活是惜惜相关的,今天我们就利用最小公倍数解决生活中的问题。
二、创设情境,引出研究问题
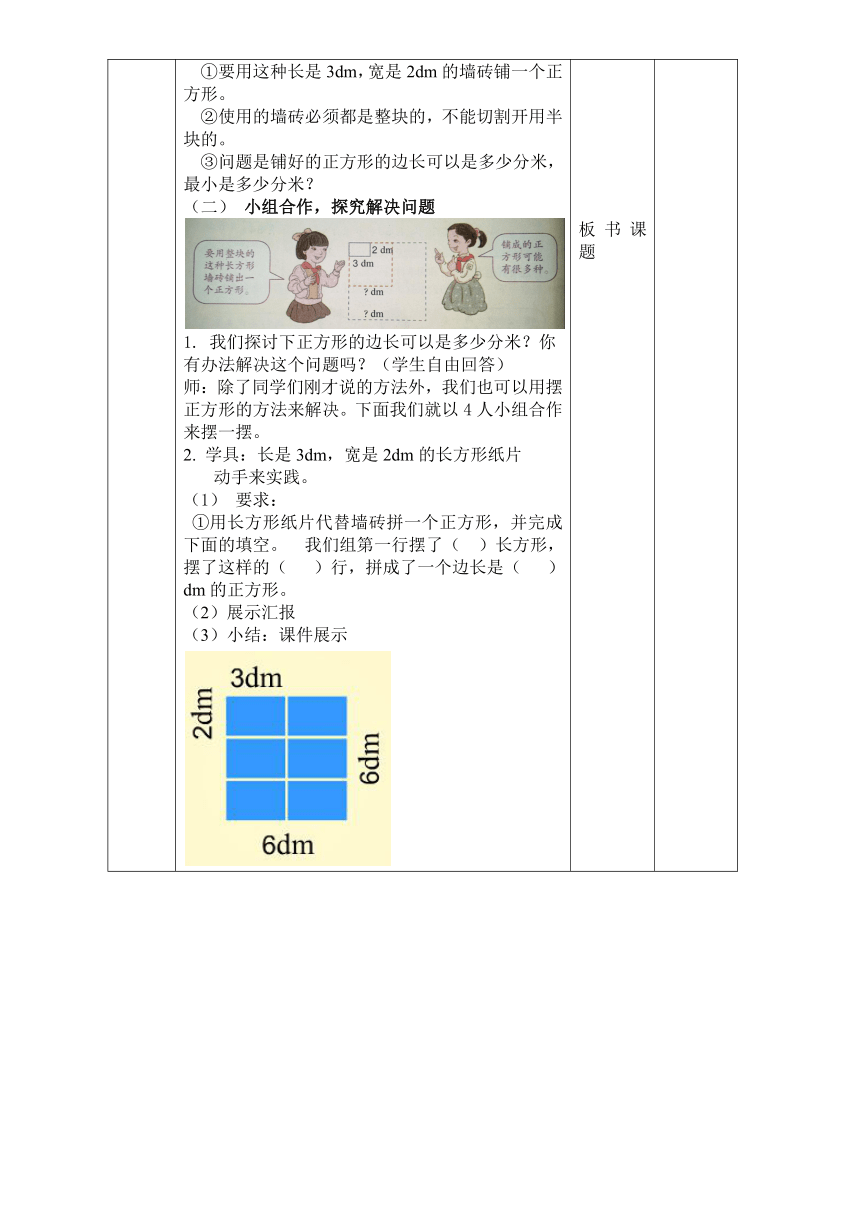
(一)出示例三
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
让学生仔细看看小明家装修的要求,获得了哪些有价值的信息?(3分钟)
①要用这种长是3dm,宽是2dm的墙砖铺一个正方形。
②使用的墙砖必须都是整块的,不能切割开用半块的。
③问题是铺好的正方形的边长可以是多少分米,最小是多少分米?
(二)
小组合作,探究解决问题
1.
我们探讨下正方形的边长可以是多少分米?你有办法解决这个问题吗?(学生自由回答)
师:除了同学们刚才说的方法外,我们也可以用摆正方形的方法来解决。下面我们就以4人小组合作来摆一摆。
2.
学具:长是3dm,宽是2dm的长方形纸片
动手来实践。
(1)
要求:
①用长方形纸片代替墙砖拼一个正方形,并完成下面的填空。
我们组第一行摆了(
)长方形,摆了这样的(
)行,拼成了一个边长是(
)dm的正方形。
(2)展示汇报
小结:课件展示
1.通过拼摆,我们发现可以铺成正方形的边长有6dm,12dm的正方形。.
2.为什么能拼成边长是6dm、12dm的正方形?
6、12与2和3有怎么样的关系?
6、12是2和3的公倍数,其中6是最小的公倍数.
学生汇报
引导学生找出6、12既是2的倍数,又是3的倍数,
师小结归纳:
因为6、12是2和3的公倍数,其中6是最小的公倍数,所以正方形的边长可以6dm,12dm,边长最小是6dm.
如果我们有足够多的小长方形的话,还可以拼出边长是其他数的正方形吗?
想一想,说一说,并小组完成习题卡(一)。(3分钟)
找出2和3的公倍数和最小公倍数(公倍数至少写3个)。
师讲解圈大数排除法:
学生汇报,师根据学生汇报板书
(9)同学们,我们发现2和3的的公倍数除了6、12,还有18,甚至更多。针对墙砖3和2的规格,分别找出3和2的公倍数和最小公倍数,就能知道所铺的正方形边长。下面我们来验证下用长3dm,宽2dm长方形,是否正好能铺满边长为18dm的正方形。(课件动态演示验证:边长为18分米的正方形)
5、总结提升:解决这个问题的关键是把铺砖问题转化成求公倍数的数学问题。
6、下面我们就用我们刚才所学的公倍数的知识解决我们生活中数学问题。
三、练一练
巩固练习(5分钟)
1、用长5dm,宽4dm的长方形墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
2.有一堆糖,4颗4颗地数,6颗6颗地数,都能刚好数完。这堆糖至少有多少颗?
3.
如果这些学生的总人数在40人以内,可能是多少人?
(
咱们可以分成
6
人一组,也可以分成
9
人一组,都正好分完。
)
4.
算一算
板书课题
课堂检测
学生完成习题卡二。(5分钟)
板书
解决问题
课后
反思
《公倍数与最小公倍数》教学反思
本节课让学生经历利用学过知识的解决问题的过程。利用公倍数、最小公倍数解决问题是为了帮助学生学习到的知识应用到生活中去,为学生提供自主探索空间的同时,鼓励学生个性化的发展,先创设情境,引出研究问题:
叔叔是做墙砖生意的。店里有许多的长3分米、宽2分米的长方形墙砖,他想用这种墙砖铺一个正方形墙面来吸引顾客。要求使用的墙砖必须使整块的,正方形的边长可以是多少分米?最小是多少分米?让学生思考这些正方形的边长可以是多少分米?
再让学生动手操作,铺正方形纸板。每个小组发放一套长3厘米、宽2厘米的小长方形纸片摆一摆进行探究。最后小组合作,探究解决问题,现场汇总各小组探究情况,让同学们在小组内交流自己的想法,认识公倍数。我们发现这样的小长方形能正好铺满边长是6厘米、12厘米的正方形。如果用这样的长方形来铺,还能铺成边长是多少厘米的正方形呢?体会解决此类问题不必每次都摆卡片。用列举法找公倍数和最小公倍数,在解决问题中渗透短除法或先找出大数的倍数,然后再在大数中圈出既是大数又是小数的公倍数。体会上述方法都有一定的局限性。而短除法可以找出任意几个数的最小公倍数。
让学生认识的找最小公倍数的应用。可以根据最小公倍数推算出其他公倍数。培养学生掌握科学高效的学习方法。
总之,本节课虽然是概念教学,但学生思维活跃,情绪高昂,学得生动有趣。老师将动手操作与抽象思维相结合,使学生在自主参与的基础上感悟、理解、应用、找出解决问题的方法。通过将实际问题转化成数学问题,培养学生分析问题和解决问题的能力。
教师
授课时间
(
)月(
)日
课时
第(
)课时
课题
最小公倍数例3
课型
新授
学习目标
1、能运用公倍数和最小公倍数的知识解决简单的实际问题。
2、通过学生动手摆一摆理解题意,并找出解决问题的方法。
3、通过将实际问题转化成数学问题,培养学生分析问题和解决问题的能力。
重点
结合具体的现实情境,体会公倍数和最小公倍数的应用。
难点
找出解决问题的方法。
教学具准备
PPT、长方形、学习卡
主备课人
教
学
过
程
一、复习引入(2分钟)
1、求出下列各数的最小公倍数。
5和7的最小公倍数(
)
12和36的最小公倍数是
(
)
4和6的最小公倍数是
(
)
2、导入新课
同学们最小公倍数跟我们的生活是惜惜相关的,今天我们就利用最小公倍数解决生活中的问题。
二、创设情境,引出研究问题
(一)出示例三
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
让学生仔细看看小明家装修的要求,获得了哪些有价值的信息?(3分钟)
①要用这种长是3dm,宽是2dm的墙砖铺一个正方形。
②使用的墙砖必须都是整块的,不能切割开用半块的。
③问题是铺好的正方形的边长可以是多少分米,最小是多少分米?
(二)
小组合作,探究解决问题
1.
我们探讨下正方形的边长可以是多少分米?你有办法解决这个问题吗?(学生自由回答)
师:除了同学们刚才说的方法外,我们也可以用摆正方形的方法来解决。下面我们就以4人小组合作来摆一摆。
2.
学具:长是3dm,宽是2dm的长方形纸片
动手来实践。
(1)
要求:
①用长方形纸片代替墙砖拼一个正方形,并完成下面的填空。
我们组第一行摆了(
)长方形,摆了这样的(
)行,拼成了一个边长是(
)dm的正方形。
(2)展示汇报
小结:课件展示
1.通过拼摆,我们发现可以铺成正方形的边长有6dm,12dm的正方形。.
2.为什么能拼成边长是6dm、12dm的正方形?
6、12与2和3有怎么样的关系?
6、12是2和3的公倍数,其中6是最小的公倍数.
学生汇报
引导学生找出6、12既是2的倍数,又是3的倍数,
师小结归纳:
因为6、12是2和3的公倍数,其中6是最小的公倍数,所以正方形的边长可以6dm,12dm,边长最小是6dm.
如果我们有足够多的小长方形的话,还可以拼出边长是其他数的正方形吗?
想一想,说一说,并小组完成习题卡(一)。(3分钟)
找出2和3的公倍数和最小公倍数(公倍数至少写3个)。
师讲解圈大数排除法:
学生汇报,师根据学生汇报板书
(9)同学们,我们发现2和3的的公倍数除了6、12,还有18,甚至更多。针对墙砖3和2的规格,分别找出3和2的公倍数和最小公倍数,就能知道所铺的正方形边长。下面我们来验证下用长3dm,宽2dm长方形,是否正好能铺满边长为18dm的正方形。(课件动态演示验证:边长为18分米的正方形)
5、总结提升:解决这个问题的关键是把铺砖问题转化成求公倍数的数学问题。
6、下面我们就用我们刚才所学的公倍数的知识解决我们生活中数学问题。
三、练一练
巩固练习(5分钟)
1、用长5dm,宽4dm的长方形墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
2.有一堆糖,4颗4颗地数,6颗6颗地数,都能刚好数完。这堆糖至少有多少颗?
3.
如果这些学生的总人数在40人以内,可能是多少人?
(
咱们可以分成
6
人一组,也可以分成
9
人一组,都正好分完。
)
4.
算一算
板书课题
课堂检测
学生完成习题卡二。(5分钟)
板书
解决问题
课后
反思
《公倍数与最小公倍数》教学反思
本节课让学生经历利用学过知识的解决问题的过程。利用公倍数、最小公倍数解决问题是为了帮助学生学习到的知识应用到生活中去,为学生提供自主探索空间的同时,鼓励学生个性化的发展,先创设情境,引出研究问题:
叔叔是做墙砖生意的。店里有许多的长3分米、宽2分米的长方形墙砖,他想用这种墙砖铺一个正方形墙面来吸引顾客。要求使用的墙砖必须使整块的,正方形的边长可以是多少分米?最小是多少分米?让学生思考这些正方形的边长可以是多少分米?
再让学生动手操作,铺正方形纸板。每个小组发放一套长3厘米、宽2厘米的小长方形纸片摆一摆进行探究。最后小组合作,探究解决问题,现场汇总各小组探究情况,让同学们在小组内交流自己的想法,认识公倍数。我们发现这样的小长方形能正好铺满边长是6厘米、12厘米的正方形。如果用这样的长方形来铺,还能铺成边长是多少厘米的正方形呢?体会解决此类问题不必每次都摆卡片。用列举法找公倍数和最小公倍数,在解决问题中渗透短除法或先找出大数的倍数,然后再在大数中圈出既是大数又是小数的公倍数。体会上述方法都有一定的局限性。而短除法可以找出任意几个数的最小公倍数。
让学生认识的找最小公倍数的应用。可以根据最小公倍数推算出其他公倍数。培养学生掌握科学高效的学习方法。
总之,本节课虽然是概念教学,但学生思维活跃,情绪高昂,学得生动有趣。老师将动手操作与抽象思维相结合,使学生在自主参与的基础上感悟、理解、应用、找出解决问题的方法。通过将实际问题转化成数学问题,培养学生分析问题和解决问题的能力。
