北师大版 八年级下册数学 1.1.1等腰三角形课件(27张PPT)
文档属性
| 名称 | 北师大版 八年级下册数学 1.1.1等腰三角形课件(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 19:25:57 | ||
图片预览







文档简介
八年级数学(下)第一章 三角形的证明
第一课时 等腰三角形
学习目标
1、了解作为证明基础的8条基本事实
2、经历“探索—发现—猜想—证明”的过程,学会综合法证明等腰三角形的有关性质定理
3、让学生学会分析几何证明题的思路、基本步骤和书写格式
4、学会根据图形的性质学会添加辅助线的规律
学习重点和难点
重点:等腰三角形的性质定理的证明
难点:用语言叙述的几何命题的证明
自学指导
阅读课本2-4页,回答下列问题:
1、回顾:作为证明基础的8条基本事实
2、运用基本事实和已学过的定理能证明三角形全等的结论么?
三角形全等的判定公理有-----------------
三角形的全等又能得到那些正确的结论--------
3、等腰三角形有哪些性质---------------------
利用已有的公理和定理证明上述结论:
总结命题证明题的思路、基本步骤和书写格式
4、 尝试证明:等边对等角。还有其他方法么?
5、根据等腰三角形的-------------得出添加辅助线的规律
6、自学检测:随堂练习和习题1、2
三角形全等
判定公理:三边对应相等的两个三角形全等(SSS)
公理:两边及其夹角对应相等的两个三角形全等(SAS)
公理:两角及其夹边对应相等的两个三角形全等(ASA)
性质公理:全等三角形的对应边、对应角相等。
你能用上面的公理证明下面的推论吗?
推论:两角及其中一角的对应边相等的两个三角形全等(AAS)
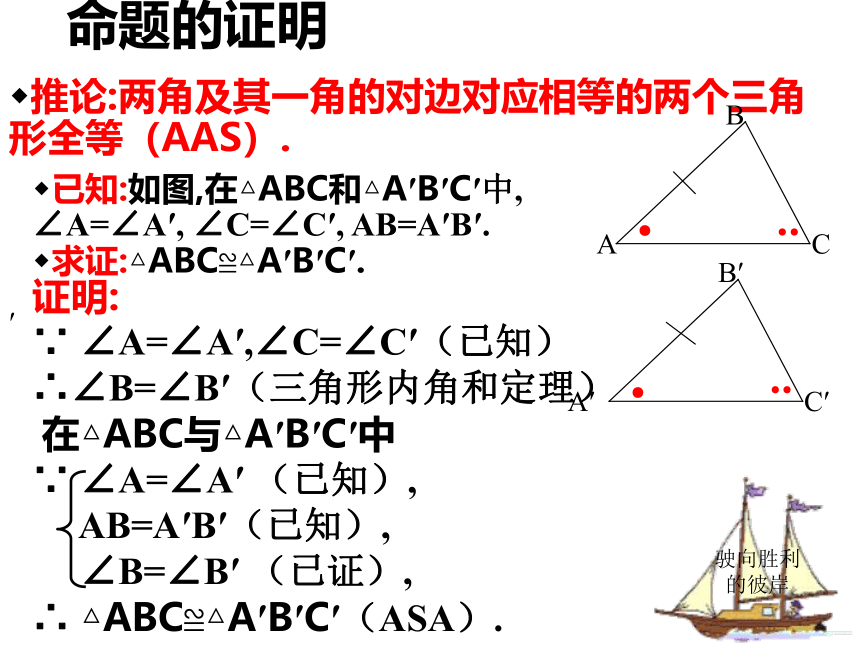
命题的证明
推论:两角及其一角的对边对应相等的两个三角形全等(AAS).
证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理)
在△ABC与△A′B′C′中
∵ ∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).
′
驶向胜利的彼岸
A
B
C
A′
B′
C′
●
●
● ●
● ●
已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.
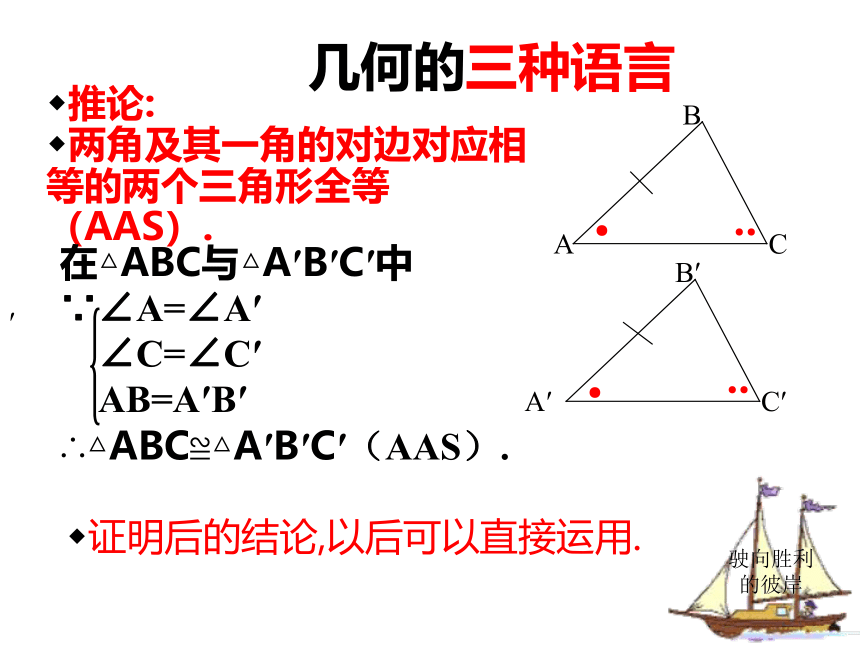
几何的三种语言
推论:
两角及其一角的对边对应相等的两个三角形全等(AAS).
在△ABC与△A′B′C′中
∵∠A=∠A′
∠C=∠C′
AB=A′B′
∴△ABC≌△A′B′C′(AAS).
′
驶向胜利的彼岸
A
B
C
A′
B′
C′
●
●
● ●
● ●
证明后的结论,以后可以直接运用.
1.如图:已知在△ABC和△DEF 中AC=DF,AB=DE,∠C=∠F=100°,则△ABC和△DEF会全等吗?若能请证明;若不能请说明理由.
A
B
C
D
E
F
其它条件不变若∠B=∠E=70°
等腰三角形的性质
你还记得我们探索过的等腰三角形的性质吗?
推论:
等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
你能利用已有的公理和定理证明这些结论吗?
议一议P2
1
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
1
2
A
C
B
D
定理 等腰三角形的两个底角相等。
这一定理可以简单叙述为:等边对等角
已知:如图,在ΔABC中,AB=AC。
求证:∠B=∠C
A
C
B
证明:取BC的中点D,连接AD。
D
∵AB=AC,BD=CD,AD=AD,
∴△ABC≌△ACD (SSS)
∴∠B=∠C (全等三角形的对应边角相等)
◆做∠BAC的平分线,交BC边于D; 过点A做AD⊥BC。
你还有其他证明方法吗 与同伴进行交流。
命题的证明
议一议P2
2
此时AD还是什么线?
胜利属于敢想敢干的人.
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
已知:
如图,在△ABC中, AB=AC.
求证: ∠B=∠C.
在Rt△ABD与Rt△ACD中
∵ AB=AC (已知),
AD=AD(公共边),
∴ △ABD≌△ACD(HL).
D
证明:
过点A作AD⊥BC,交BC于点D.
∴ ∠B=∠C(全等三角形的对应角相等).
几何的三种语言
议一议P2
3
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
证明后的结论,以后可以直接运用.
推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
A
C
B
D
1
2
∵AB=AC, ∠1=∠2(已知).
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC, BD=CD (已知).
∴∠1=∠2,AD⊥BC(等腰三角形三线合一)
∵AB=AC, AD⊥BC(已知).
∴BD=CD, ∠1=∠2(等腰三角形三线合一)
轮换条件∠1=∠2, AD⊥BC,BD=CD,可得三线合一的三种不同形式的运用.
知识的巩固
◆证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
1.如图,在三角形ABD中,C是BD上的一点,
且AC垂直BD,AC=BC=CD.
(1) 求证:△ABD是等腰三角形
(2)求∠ABD的度数
A
B
C
D
开拓思维
1.将下面证明中每一步的理由写在括号内:
已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.
证明:连接BD,
在△BAD和△DCB中,
∵ AB=CD( )
AD=CB( )
BD=DB( )
∴ △BAD≌ △DCB( )
∴ :∠A=∠C ( )
A
B
C
D
2.已知:如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D
A
B
C
D
E
F
等腰三角形△ABC,AB=AC,BD⊥AC
探索∠DBC与∠A之间关系?
┏
A
B
C
D
探索与拓展
等腰三角形△ABC,AB=AC, DE⊥AC, DF⊥AB, CH⊥AB
探索DE、DF、 CH的关系?
A
B
C
A
B
C
D
┓
┓
┓
等腰三角形底边上的点到两腰的距离和等于一腰上的高
E
F
H
D
┓
┓
┓
E
F
H
DE+DF=CH
演示
A
B
C
方法1:在HC上取一点G,使FD=HG
D
┓
┓
┓
E
F
H
●
G
DE+DF=CH
A
B
C
方法2:过D点作DG∥HF
D
┓
┓
┓
E
F
H
●
G
DE+DF=CH
A
B
C
D
┓
┓
┓
E
F
H
●
G
DE+DF=CH
方法3:过D点作DG⊥HF
还有好方法吗?
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
已知:
如图,在△ABC中, AB=AC.
求证: ∠B=∠C.
在Rt△ABD与Rt△ACD中
∵ AB=AC (已知),
AD=AD(公共边),
∴ △ABD≌△ACD(HL).
D
证明:
过点A作AD⊥BC,交BC于点D.
∴ ∠B=∠C(全等三角形的对应角相等).
几何的三种语言
议一议P2
3
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
证明后的结论,以后可以直接运用.
第一课时 等腰三角形
学习目标
1、了解作为证明基础的8条基本事实
2、经历“探索—发现—猜想—证明”的过程,学会综合法证明等腰三角形的有关性质定理
3、让学生学会分析几何证明题的思路、基本步骤和书写格式
4、学会根据图形的性质学会添加辅助线的规律
学习重点和难点
重点:等腰三角形的性质定理的证明
难点:用语言叙述的几何命题的证明
自学指导
阅读课本2-4页,回答下列问题:
1、回顾:作为证明基础的8条基本事实
2、运用基本事实和已学过的定理能证明三角形全等的结论么?
三角形全等的判定公理有-----------------
三角形的全等又能得到那些正确的结论--------
3、等腰三角形有哪些性质---------------------
利用已有的公理和定理证明上述结论:
总结命题证明题的思路、基本步骤和书写格式
4、 尝试证明:等边对等角。还有其他方法么?
5、根据等腰三角形的-------------得出添加辅助线的规律
6、自学检测:随堂练习和习题1、2
三角形全等
判定公理:三边对应相等的两个三角形全等(SSS)
公理:两边及其夹角对应相等的两个三角形全等(SAS)
公理:两角及其夹边对应相等的两个三角形全等(ASA)
性质公理:全等三角形的对应边、对应角相等。
你能用上面的公理证明下面的推论吗?
推论:两角及其中一角的对应边相等的两个三角形全等(AAS)
命题的证明
推论:两角及其一角的对边对应相等的两个三角形全等(AAS).
证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理)
在△ABC与△A′B′C′中
∵ ∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).
′
驶向胜利的彼岸
A
B
C
A′
B′
C′
●
●
● ●
● ●
已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.
几何的三种语言
推论:
两角及其一角的对边对应相等的两个三角形全等(AAS).
在△ABC与△A′B′C′中
∵∠A=∠A′
∠C=∠C′
AB=A′B′
∴△ABC≌△A′B′C′(AAS).
′
驶向胜利的彼岸
A
B
C
A′
B′
C′
●
●
● ●
● ●
证明后的结论,以后可以直接运用.
1.如图:已知在△ABC和△DEF 中AC=DF,AB=DE,∠C=∠F=100°,则△ABC和△DEF会全等吗?若能请证明;若不能请说明理由.
A
B
C
D
E
F
其它条件不变若∠B=∠E=70°
等腰三角形的性质
你还记得我们探索过的等腰三角形的性质吗?
推论:
等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
你能利用已有的公理和定理证明这些结论吗?
议一议P2
1
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
1
2
A
C
B
D
定理 等腰三角形的两个底角相等。
这一定理可以简单叙述为:等边对等角
已知:如图,在ΔABC中,AB=AC。
求证:∠B=∠C
A
C
B
证明:取BC的中点D,连接AD。
D
∵AB=AC,BD=CD,AD=AD,
∴△ABC≌△ACD (SSS)
∴∠B=∠C (全等三角形的对应边角相等)
◆做∠BAC的平分线,交BC边于D; 过点A做AD⊥BC。
你还有其他证明方法吗 与同伴进行交流。
命题的证明
议一议P2
2
此时AD还是什么线?
胜利属于敢想敢干的人.
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
已知:
如图,在△ABC中, AB=AC.
求证: ∠B=∠C.
在Rt△ABD与Rt△ACD中
∵ AB=AC (已知),
AD=AD(公共边),
∴ △ABD≌△ACD(HL).
D
证明:
过点A作AD⊥BC,交BC于点D.
∴ ∠B=∠C(全等三角形的对应角相等).
几何的三种语言
议一议P2
3
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
证明后的结论,以后可以直接运用.
推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
A
C
B
D
1
2
∵AB=AC, ∠1=∠2(已知).
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC, BD=CD (已知).
∴∠1=∠2,AD⊥BC(等腰三角形三线合一)
∵AB=AC, AD⊥BC(已知).
∴BD=CD, ∠1=∠2(等腰三角形三线合一)
轮换条件∠1=∠2, AD⊥BC,BD=CD,可得三线合一的三种不同形式的运用.
知识的巩固
◆证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
1.如图,在三角形ABD中,C是BD上的一点,
且AC垂直BD,AC=BC=CD.
(1) 求证:△ABD是等腰三角形
(2)求∠ABD的度数
A
B
C
D
开拓思维
1.将下面证明中每一步的理由写在括号内:
已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.
证明:连接BD,
在△BAD和△DCB中,
∵ AB=CD( )
AD=CB( )
BD=DB( )
∴ △BAD≌ △DCB( )
∴ :∠A=∠C ( )
A
B
C
D
2.已知:如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D
A
B
C
D
E
F
等腰三角形△ABC,AB=AC,BD⊥AC
探索∠DBC与∠A之间关系?
┏
A
B
C
D
探索与拓展
等腰三角形△ABC,AB=AC, DE⊥AC, DF⊥AB, CH⊥AB
探索DE、DF、 CH的关系?
A
B
C
A
B
C
D
┓
┓
┓
等腰三角形底边上的点到两腰的距离和等于一腰上的高
E
F
H
D
┓
┓
┓
E
F
H
DE+DF=CH
演示
A
B
C
方法1:在HC上取一点G,使FD=HG
D
┓
┓
┓
E
F
H
●
G
DE+DF=CH
A
B
C
方法2:过D点作DG∥HF
D
┓
┓
┓
E
F
H
●
G
DE+DF=CH
A
B
C
D
┓
┓
┓
E
F
H
●
G
DE+DF=CH
方法3:过D点作DG⊥HF
还有好方法吗?
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
已知:
如图,在△ABC中, AB=AC.
求证: ∠B=∠C.
在Rt△ABD与Rt△ACD中
∵ AB=AC (已知),
AD=AD(公共边),
∴ △ABD≌△ACD(HL).
D
证明:
过点A作AD⊥BC,交BC于点D.
∴ ∠B=∠C(全等三角形的对应角相等).
几何的三种语言
议一议P2
3
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
证明后的结论,以后可以直接运用.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
