北师大版八年级上册数学7.5.1三角形内角和定理证明课件(共27张PPT)
文档属性
| 名称 | 北师大版八年级上册数学7.5.1三角形内角和定理证明课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 19:49:48 | ||
图片预览







文档简介
7.5三角形内角和定理
猜谜语
形状似如山,稳定性能坚。
三竿首尾连,学问不简单。
打一图形名称( )
三角形
问题1:你还记得吗?小学我们是怎样探索三角形内角和的?你能给大家说说或者展示一下吗?
创设情境,引入新课
锐角三角形
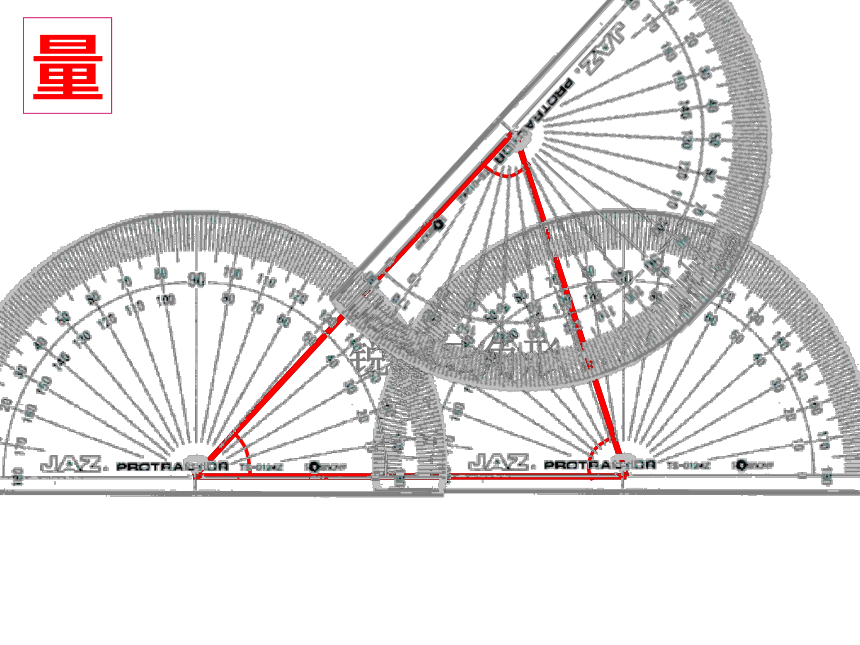
量
3
2
3
1
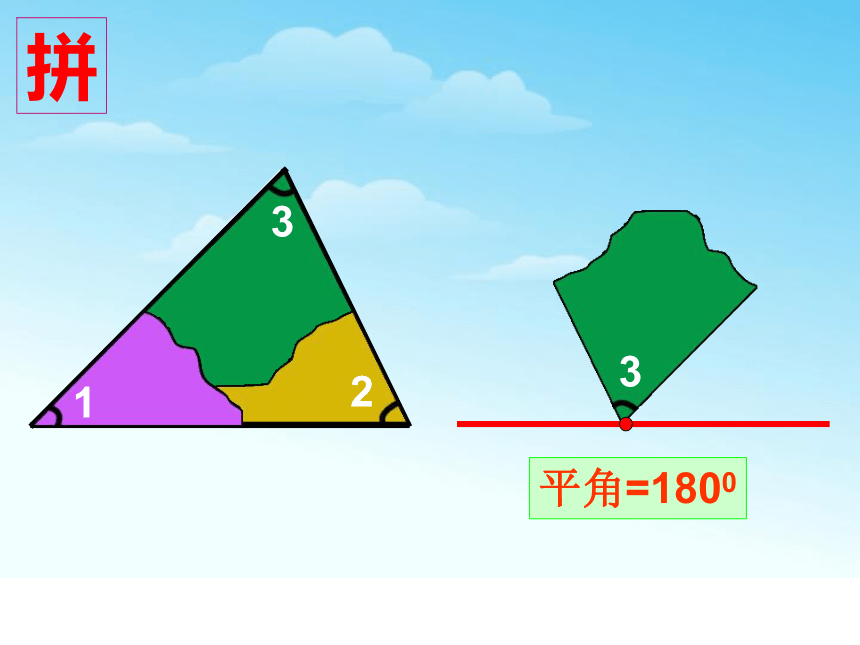
平角=1800
拼
1
1
2
2
3
3
折
问题2:小学的证明方法固然好,但是这些方法可靠吗?现在的你有更加科学严密、更有说服力 的证明方法吗?
创设情境,引入新课
证明几何命题的一般步骤:
(1)根据题意,画出图形;
(2)结合图形,根据条件结论,写出“已知”和“求证”;
(3)找出由已知推出求证的途径,写出“证明”。
你能用数学语言写出这一证明过程吗?
三角形的内角和等于180°
这一命题的条件是__________________________
结论是_________________________
三个角是一个三角形的内角
这三个角的和等于180°
方法一:
A
B
C
已知:如图,△ABC .
求证:∠A +∠B +∠C =180°.
证明:延长BC到D,过点C作CE∥AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
又∵∠1+∠2+∠3=180° (平角的定义)
∴ ∠A+∠B+∠ACB=180° (等量代换)
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
问题:你还能用其他的推理方法证明三角形内角和定理吗?
方法二:
A
B
C
A
B
C
P
Q
2
3
1
证明:过点A作直线PQ∥BC则
∠1=∠B
∠2=∠C (两直线平行,内错角相等)
又∵∠1+∠2+∠3=180° (平角的定义)
∴ ∠BAC+∠B+∠C=180°(等量代换)
问题:你还能用其他的推理方法证明三角形内角和定理吗?
A
C
B
A
C
B
D
D
A
C
B
1
2
旋转平移
规范作图
自主学习,合作探究
2.小小辅助线,作时画虚线,
写清其来源,隐藏条件见.
1.添加辅助线的目的:
添加辅助线
三角形
内角和
转化
平角、同旁内角
典例解析,应用新知
例1 如图,在△ABC中∠B=38°,
∠C=62°,AD是△ABC的角平分线,
求∠ADB的度数.
如图,在△ABC中,∠B=380 ,∠C=620,AD是△ABC的角平分线,求∠ADB的度数。
A
D
C
B
三角形内角和定理
BAC
ADB
ADB
三角形内角和定理
已知
已证
等式的性质
等式的性质
角平分线
1.在△ABC中,∠A的度数是∠B的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
列方程解答
在△ABC中,∠A的度数是∠B的度数的3倍,
∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解 设∠B为x °则∠A为(3x)°,∠C为(x+ 15)°
3x+x+(x+15)=180
解得 x=33
所以 3x=99 ,x+15 =48
答:∠A,∠B,∠C的度数分别为99°,33°,48°.
根据三角形的内角和等于180° 得:
2.根据所学的知识,你能想办法求出下列图形的内角和吗?
3、如图:∠α= 。
280
480
320
α
440
4.如图,求?A1+?A2+?A3+?A4+?A5的度数。
A2
A1
A5
A3
A4
2
1
少年帕斯卡与“三角形内角和”
帕斯卡:(BlaisePascal,1623~1662)法国著名的数学家、物理学家、哲学家和散文家,近代概率论的奠基者.帕斯卡没有受过正规的学校教育.他4岁时母亲病故,帕斯卡从小就对数学感兴趣. 有一天他问父亲,什么是几何,父亲很简单地回答说“几何就是教人在画图时能作出正确又美观的图”.于是帕斯卡就拿了粉笔在地上画起各种图形来.画着画着,12岁的帕斯卡独自发现任何一个三角形内角和都是180度,当他把这个发现告诉父亲时,父亲激动得泪如雨下. 帕斯卡精通欧几里得几何,他自己独立地发现了欧几里得的前32条定理,在我们以后学习的数学知识中,有很多定理都是帕斯卡发现和证明的.
小结
本节课“我知道了…”,
“我发现了…”,
“我学会了…”,
“我想我以后将…”
定理
证明方法
计算
应用
A . 课本P179页1.2.3题
布置作业,落实新知
猜谜语
形状似如山,稳定性能坚。
三竿首尾连,学问不简单。
打一图形名称( )
三角形
问题1:你还记得吗?小学我们是怎样探索三角形内角和的?你能给大家说说或者展示一下吗?
创设情境,引入新课
锐角三角形
量
3
2
3
1
平角=1800
拼
1
1
2
2
3
3
折
问题2:小学的证明方法固然好,但是这些方法可靠吗?现在的你有更加科学严密、更有说服力 的证明方法吗?
创设情境,引入新课
证明几何命题的一般步骤:
(1)根据题意,画出图形;
(2)结合图形,根据条件结论,写出“已知”和“求证”;
(3)找出由已知推出求证的途径,写出“证明”。
你能用数学语言写出这一证明过程吗?
三角形的内角和等于180°
这一命题的条件是__________________________
结论是_________________________
三个角是一个三角形的内角
这三个角的和等于180°
方法一:
A
B
C
已知:如图,△ABC .
求证:∠A +∠B +∠C =180°.
证明:延长BC到D,过点C作CE∥AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
又∵∠1+∠2+∠3=180° (平角的定义)
∴ ∠A+∠B+∠ACB=180° (等量代换)
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
问题:你还能用其他的推理方法证明三角形内角和定理吗?
方法二:
A
B
C
A
B
C
P
Q
2
3
1
证明:过点A作直线PQ∥BC则
∠1=∠B
∠2=∠C (两直线平行,内错角相等)
又∵∠1+∠2+∠3=180° (平角的定义)
∴ ∠BAC+∠B+∠C=180°(等量代换)
问题:你还能用其他的推理方法证明三角形内角和定理吗?
A
C
B
A
C
B
D
D
A
C
B
1
2
旋转平移
规范作图
自主学习,合作探究
2.小小辅助线,作时画虚线,
写清其来源,隐藏条件见.
1.添加辅助线的目的:
添加辅助线
三角形
内角和
转化
平角、同旁内角
典例解析,应用新知
例1 如图,在△ABC中∠B=38°,
∠C=62°,AD是△ABC的角平分线,
求∠ADB的度数.
如图,在△ABC中,∠B=380 ,∠C=620,AD是△ABC的角平分线,求∠ADB的度数。
A
D
C
B
三角形内角和定理
BAC
ADB
ADB
三角形内角和定理
已知
已证
等式的性质
等式的性质
角平分线
1.在△ABC中,∠A的度数是∠B的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
列方程解答
在△ABC中,∠A的度数是∠B的度数的3倍,
∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解 设∠B为x °则∠A为(3x)°,∠C为(x+ 15)°
3x+x+(x+15)=180
解得 x=33
所以 3x=99 ,x+15 =48
答:∠A,∠B,∠C的度数分别为99°,33°,48°.
根据三角形的内角和等于180° 得:
2.根据所学的知识,你能想办法求出下列图形的内角和吗?
3、如图:∠α= 。
280
480
320
α
440
4.如图,求?A1+?A2+?A3+?A4+?A5的度数。
A2
A1
A5
A3
A4
2
1
少年帕斯卡与“三角形内角和”
帕斯卡:(BlaisePascal,1623~1662)法国著名的数学家、物理学家、哲学家和散文家,近代概率论的奠基者.帕斯卡没有受过正规的学校教育.他4岁时母亲病故,帕斯卡从小就对数学感兴趣. 有一天他问父亲,什么是几何,父亲很简单地回答说“几何就是教人在画图时能作出正确又美观的图”.于是帕斯卡就拿了粉笔在地上画起各种图形来.画着画着,12岁的帕斯卡独自发现任何一个三角形内角和都是180度,当他把这个发现告诉父亲时,父亲激动得泪如雨下. 帕斯卡精通欧几里得几何,他自己独立地发现了欧几里得的前32条定理,在我们以后学习的数学知识中,有很多定理都是帕斯卡发现和证明的.
小结
本节课“我知道了…”,
“我发现了…”,
“我学会了…”,
“我想我以后将…”
定理
证明方法
计算
应用
A . 课本P179页1.2.3题
布置作业,落实新知
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
