北师大版八年级数学上册6.2中位数与众数 课件(共29张PPT)
文档属性
| 名称 | 北师大版八年级数学上册6.2中位数与众数 课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览




文档简介
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
6.2中 位 数 和 众 数
heiyazi.mp3
招聘启事
本公司需要招聘技术员一人, 有意者请来公司面试。
本山公司人事部
2010年4月1日
这个公司员工收入到底怎样?
我这里报酬不错, 月平均工资是2000元,你在这里好好干!
赵经理
应聘者小范
第二天,小范上班了。
职员C
我的工资是1500元,在公司算中等收入
职员D
我们好几个人工资都是1200元
小范在公司工作了一周后
你欺骗了我,我已问过其他技术员,没有一个技术员的工资超过2000元.
平均工资确实是每月2000元,你看看公司的工资报表.
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资(元)
5000
4000
1800
1700
1500
1200
1200
1200
400
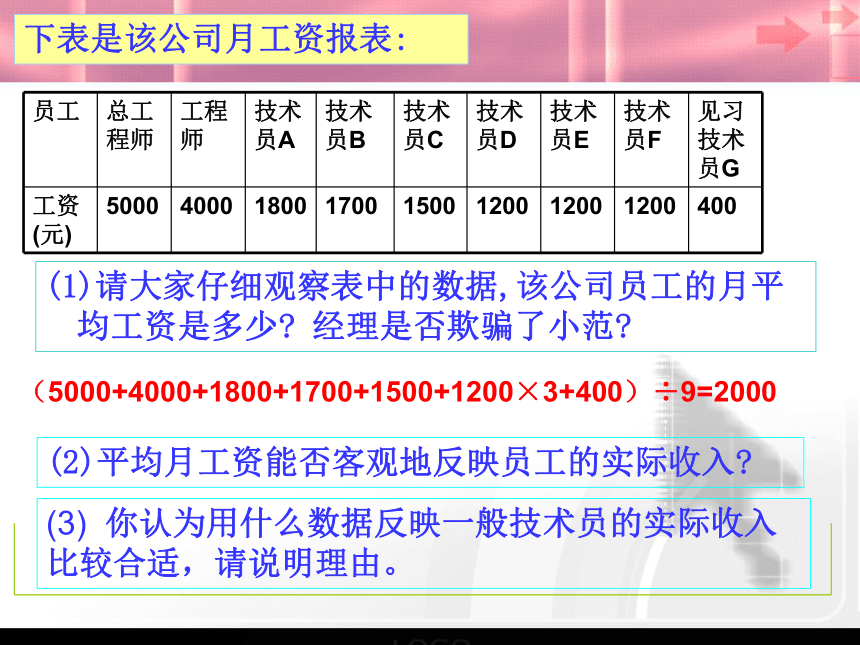
下表是该公司月工资报表:
请大家仔细观察表中的数据,该公司员工的月平均工资是多少? 经理是否欺骗了小范?
平均月工资能否客观地反映员工的实际收入?
(3) 你认为用什么数据反映一般技术员的实际收入比较合适,请说明理由。
(5000+4000+1800+1700+1500+1200×3+400)÷9=2000
中位数定义:
众数的定义:
在一组数据中,出现次数最多的数据叫做这组数据的众数。
如上表中的1200(元)
中位数
众数
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资
5000
4000
1800
1700
1500
1200
1200
1200
400
将一组数据按大小依次排列,把处在最中间位置的一个
数据叫做这组数据的中位数。
职员C
我的工资是1500元,在公司算中等收入
职员D
我们好几个人工资都是1200元
中位数定义:
中位数
众 数
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资(元)
5000
4000
1800
1700
1500
1200
1200
1200
400
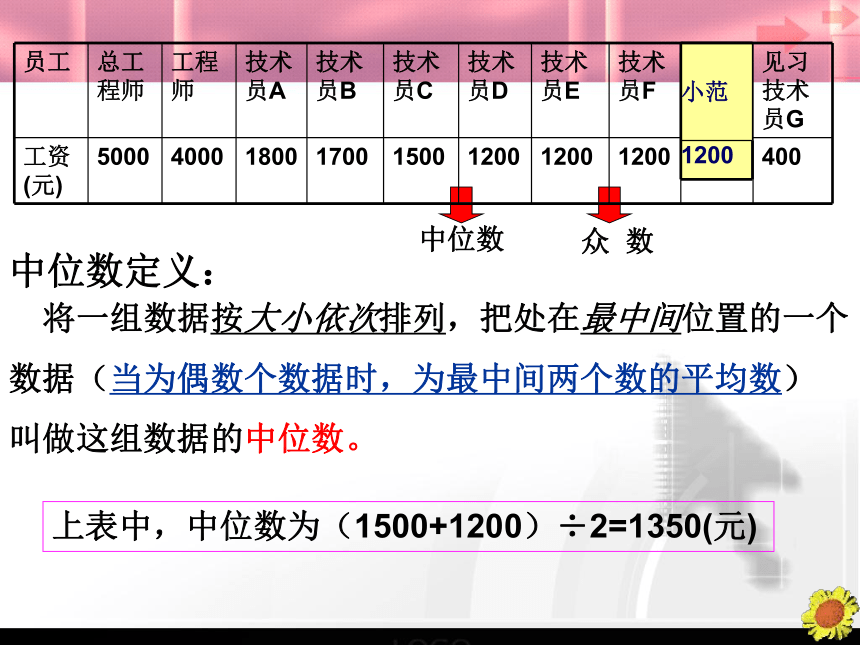
将一组数据按大小依次排列,把处在最中间位置的一个
数据(当为偶数个数据时,为最中间两个数的平均数)
叫做这组数据的中位数。
小范
1200
上表中,中位数为(1500+1200)÷2=1350(元)
中位数
众数
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资(元)
5000
4000
1800
1700
1500
1200
1200
1200
400
小范
1200
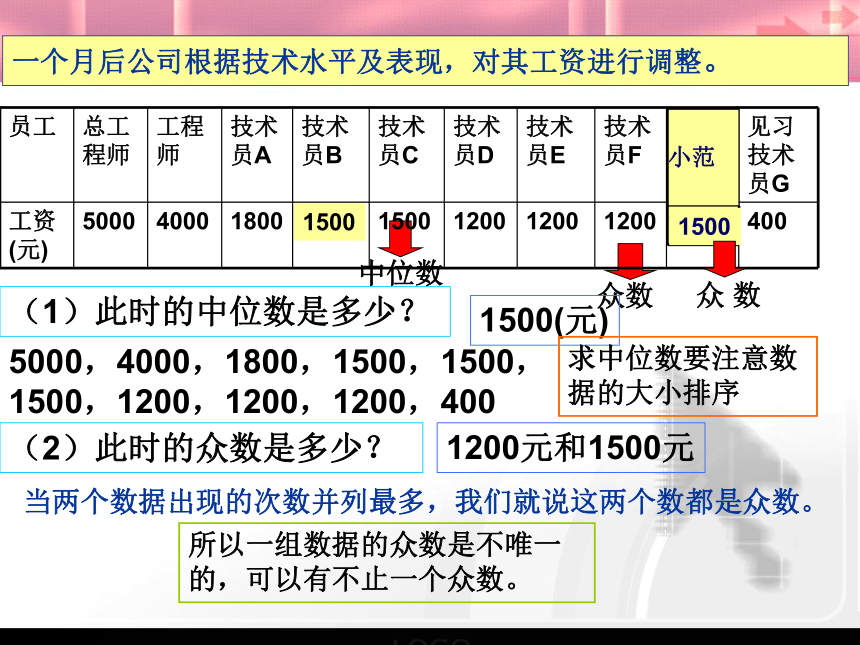
一个月后公司根据技术水平及表现,对其工资进行调整。
1500
1500
(1)此时的中位数是多少?
5000,4000,1800,1500,1500,1500,1200,1200,1200,400
1500(元)
(2)此时的众数是多少?
众 数
当两个数据出现的次数并列最多,我们就说这两个数都是众数。
1200元和1500元
所以一组数据的众数是不唯一的,可以有不止一个众数。
求中位数要注意数据的大小排序
600
?
750
750
800
850
900
1500
2100
明明妈妈加工资后,这组数据的平均数、中位数会跟着变化吗?
平均数:一组数据中的一个数发生变化,
这组数据的平均数一定发生变化。
中位数:一组数据中的一个数发生变化,
这组数据的中位数不一定会发生变化。
中位数
3,3,2,3,5,3,10,3
1,4,3,2,4,5
3, 7, 9, 2, 4, 6, 2
2,3,-1,2,1,3,0
众数
中位数
数据
2
2,3
3.5
4
3
3
4
2
在导学案上完成基础练习
1,求下列各组数据的中位数和众数:
-1 , 0 , 1 , 2 , 2 , 3 , 3
9 , 7 , 6 , 4 , 3 , 2 , 2
1 , 2 , 3 , 4 , 4 , 5
10 , 5 , 3 , 3 , 3 , 3 , 3 , 2
排序:
排序:
排序:
排序:
结合“基础练习”
完成合作探秘
如果数据个数n为奇数时,第
个数据为中位数;如果数据 个数n
为偶数时,第 和 个数据的
平均数为中位数.
(1)一组数据的中位数只有一个。
(2)一组数据的中位数一定是这组数
据中的某个数据。
(3)一组数据的众数只有一个。
(4)一组数据的众数一定是这组数据
中的某个数 。
(5)一组数据的中位数、众数可以是同
一个数据。
√
×
√
√
×
2,下列说法是否正确?
如果错误,请说明理由。
红星电子配件厂第一生产组有7名工人,每人的日均生产零件个数是:11,7,13,19,13,13,15
求这组数据的平均数、中位数和众数。
当一组数据中没有特别大或特别小的数据出现时,这组数据的平均数、中位数和众数会非常接近。
13,
求下列各组数据的中位数
2
15,
19,
23,
5,
12,15,30,18,30
40,35,62,40,99,62
1,2,3,4,5,6,7
求下列各组数据的众数
计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,在现实生活中较为常用。但容易受极端值的影响。
中位数的优点是计算简单,只与其在数据中的位置有关,受极端值的影响较小。但不能充分利用所有的数据信息。
众数只与其在数据中重复的次数有关,而且往往不是唯一的。 但不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
平均数、中位数和众数都是描述数据集中趋势的统计量
议一议
平均数、中位数和众数有哪些特征?
谈谈学习本节课有什么体会与收获?
学习本节课内容后,你在今后的生活中对待一 些事情进行分析时,对你会有什么帮助?
必做 :作业本
选做:请统计班级里每位同学期望的数学回家作业时间,求出平均数、中位数和众数,根据你所统计的数据及分析结果,向数学老师提交一份建议书。
附表:
作业时间
10分
15分
20分
30分
40分
40分以上
人数(人)
1、下面数据的中位数和众数各是多少?
8,10,10,13,13,13,14,15,17,18,19
3,3,2,3,5,3,10,3
1,4,3,2,4,5
3, 7, 9, 2, 4, 6, 2
2,3,-1,2,1,3,0
众数
中位数
数据
2
2,3
3.5
4
3
3
4
2
在导学案上完成基础练习
1,求下列各组数据的中位数和众数:
-1 , 0 , 1 , 2 , 2 , 3 , 3
9 , 7 , 6 , 4 , 3 , 2 , 2
1 , 2 , 3 , 4 , 4 , 5
10 , 5 , 3 , 3 , 3 , 3 , 3 , 2
排序:
排序:
排序:
排序:
议一议:通过这个练习你能说说中位数和众数的特性吗?
20
20
21
3
20
20
5
练一练
20和35
数 据
中位数
众数
15,20,20,22,35
?
?
-100,20,20,22,1000
?
?
15,20,20,22,35,38
?
?
15,20,20,22,35,35
?
?
-3,0,1,5,5,3,14
?
?
21
20
特性:
4、众数是一组数据中出现次数最多的数据,一定 是这组数据中的某个数据,单位与数据的单位相同。
5、一组数据中的众数有时不只一个,如数据2、 3、-1、2、1、3中,2和3都出现了2次,它们都是这组数据的众数。
1、中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是。
2、求中位数时要将一组数据按大小顺序排列,若这组数据是奇数个,则最中间的数据是中位数,若这组数据是偶数个,则最中间的两个数的平均数是中位数。
3、中位数的单位与数据单位相同。
1、在歌手大奖赛中,去掉一个最高分和一个最低分,将剩下的分数的平均数作为这位歌手的最后得分,为什么?
2、如果在一次考试中,全班同学的成绩的中位数是75分,你恰好得了75分,你知道自己的成绩在全班的位置吗?如果全班同学的成绩的平均分是75分呢?
3、在公园做游戏的一群人的年龄分别为4,5,5,5,4,5,5,6,28,50这组数据的众数为多少?平均数为多少?哪个更有代表性?
平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动,容易受极端值的影响;
中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量,但出现多个众数时,就没多大意义了;
平均数、中位数及众数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。
平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动,容易受极端值的影响;
中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量,但出现多个众数时,就没多大意义了;
平均数、中位数及众数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。
补充练习: 在一次中学生田径运动会上,
参加男子跳高的17名运动员的成绩如下表所示:
成绩(米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的中位数与众数。
2,某班50名学生中,13岁6人,14岁的25人,
15岁的16人,16岁的3人。那么,这个班同
学年龄的众数和中位数分别是( )
A,13,16 B,14,11 C,14,14 D,14,16
C
3人
16人
25人
6人
出现次数
16岁
15岁
14岁
13岁
数据
排序:
13,…,13, 14,…,14, 15,…,15, 16,…,16
6个
25个
16个
3个
第25和第26个数据
红星电子配件厂第一生产组有7名工人,每人的日均生产零件个数是:11,7,13,19,13,13,15
求这组数据的平均数、中位数和众数。
当一组数据中没有特别大或特别小的数据出现时,这组数据的平均数、中位数和众数会非常接近。
1、小明的期中考试成绩(单位 :分)
78,87,96,78,80,95,75
求这一组数据的中位数是 ,
众数是 。
完成导学案上面“当堂检测1,2”
80分
78分
中位数——排序 取中间
众 数——出现次数最多
2,某班50名学生中,13岁6人,14岁的25人,
15岁的16人,16岁的3人。那么,这个班同
学年龄的众数和中位数分别是( )
A,13,16 B,14,11 C,14,14 D,14,16
C
3人
16人
25人
6人
出现次数
16岁
15岁
14岁
13岁
数据
排序:
13,…,13, 14,…,14, 15,…,15, 16,…,16
6个
25个
16个
3个
第25和第26个数据
3、一组数据23,27,20,18, ,12.
它的中位数是21,求x的值。
排序:12, 18, 20, 23, 27
X,
X,
完成导学案上面“当堂检测3,4”
4、当5个整数从小到大排列,其中位数
是4,如果这组数据的唯一众数是6,
则5个整数可能的最大的和是( )
A、21 B、22
C、23 D、24
A
红星电子配件厂第一生产组有7名工人,每人的日均生产零件个数是:11,7,13,19,13,13,15
求这组数据的平均数、中位数和众数。
当一组数据中没有特别大或特别小的数据出现时,这组数据的平均数、中位数和众数会非常接近。
1
3
7
11
5
2
1
数量/双
25
24.5
24
23.5
23
22.5
22
尺码/厘米
某商店销售一批女鞋 30 双,其中各种尺码的
销售量如下表:(单位:双)
(1)计算30双女鞋尺码的平均数、中位数和众数。
(2)在(1)中所求的三个数据中,你认为鞋店老板
最感兴趣的是哪一个?说说你的理由。
做一做
13,
求下列各组数据的中位数
2
15,
19,
23,
5,
12,15,30,18,30
40,35,62,40,99,62
1,2,3,4,5,6,7
求下列各组数据的众数
单击此处编辑母版副标题样式
*
*
*
6.2中 位 数 和 众 数
heiyazi.mp3
招聘启事
本公司需要招聘技术员一人, 有意者请来公司面试。
本山公司人事部
2010年4月1日
这个公司员工收入到底怎样?
我这里报酬不错, 月平均工资是2000元,你在这里好好干!
赵经理
应聘者小范
第二天,小范上班了。
职员C
我的工资是1500元,在公司算中等收入
职员D
我们好几个人工资都是1200元
小范在公司工作了一周后
你欺骗了我,我已问过其他技术员,没有一个技术员的工资超过2000元.
平均工资确实是每月2000元,你看看公司的工资报表.
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资(元)
5000
4000
1800
1700
1500
1200
1200
1200
400
下表是该公司月工资报表:
请大家仔细观察表中的数据,该公司员工的月平均工资是多少? 经理是否欺骗了小范?
平均月工资能否客观地反映员工的实际收入?
(3) 你认为用什么数据反映一般技术员的实际收入比较合适,请说明理由。
(5000+4000+1800+1700+1500+1200×3+400)÷9=2000
中位数定义:
众数的定义:
在一组数据中,出现次数最多的数据叫做这组数据的众数。
如上表中的1200(元)
中位数
众数
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资
5000
4000
1800
1700
1500
1200
1200
1200
400
将一组数据按大小依次排列,把处在最中间位置的一个
数据叫做这组数据的中位数。
职员C
我的工资是1500元,在公司算中等收入
职员D
我们好几个人工资都是1200元
中位数定义:
中位数
众 数
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资(元)
5000
4000
1800
1700
1500
1200
1200
1200
400
将一组数据按大小依次排列,把处在最中间位置的一个
数据(当为偶数个数据时,为最中间两个数的平均数)
叫做这组数据的中位数。
小范
1200
上表中,中位数为(1500+1200)÷2=1350(元)
中位数
众数
员工
总工程师
工程师
技术员A
技术员B
技术员C
技术员D
技术员E
技术员F
见习技术员G
工资(元)
5000
4000
1800
1700
1500
1200
1200
1200
400
小范
1200
一个月后公司根据技术水平及表现,对其工资进行调整。
1500
1500
(1)此时的中位数是多少?
5000,4000,1800,1500,1500,1500,1200,1200,1200,400
1500(元)
(2)此时的众数是多少?
众 数
当两个数据出现的次数并列最多,我们就说这两个数都是众数。
1200元和1500元
所以一组数据的众数是不唯一的,可以有不止一个众数。
求中位数要注意数据的大小排序
600
?
750
750
800
850
900
1500
2100
明明妈妈加工资后,这组数据的平均数、中位数会跟着变化吗?
平均数:一组数据中的一个数发生变化,
这组数据的平均数一定发生变化。
中位数:一组数据中的一个数发生变化,
这组数据的中位数不一定会发生变化。
中位数
3,3,2,3,5,3,10,3
1,4,3,2,4,5
3, 7, 9, 2, 4, 6, 2
2,3,-1,2,1,3,0
众数
中位数
数据
2
2,3
3.5
4
3
3
4
2
在导学案上完成基础练习
1,求下列各组数据的中位数和众数:
-1 , 0 , 1 , 2 , 2 , 3 , 3
9 , 7 , 6 , 4 , 3 , 2 , 2
1 , 2 , 3 , 4 , 4 , 5
10 , 5 , 3 , 3 , 3 , 3 , 3 , 2
排序:
排序:
排序:
排序:
结合“基础练习”
完成合作探秘
如果数据个数n为奇数时,第
个数据为中位数;如果数据 个数n
为偶数时,第 和 个数据的
平均数为中位数.
(1)一组数据的中位数只有一个。
(2)一组数据的中位数一定是这组数
据中的某个数据。
(3)一组数据的众数只有一个。
(4)一组数据的众数一定是这组数据
中的某个数 。
(5)一组数据的中位数、众数可以是同
一个数据。
√
×
√
√
×
2,下列说法是否正确?
如果错误,请说明理由。
红星电子配件厂第一生产组有7名工人,每人的日均生产零件个数是:11,7,13,19,13,13,15
求这组数据的平均数、中位数和众数。
当一组数据中没有特别大或特别小的数据出现时,这组数据的平均数、中位数和众数会非常接近。
13,
求下列各组数据的中位数
2
15,
19,
23,
5,
12,15,30,18,30
40,35,62,40,99,62
1,2,3,4,5,6,7
求下列各组数据的众数
计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,在现实生活中较为常用。但容易受极端值的影响。
中位数的优点是计算简单,只与其在数据中的位置有关,受极端值的影响较小。但不能充分利用所有的数据信息。
众数只与其在数据中重复的次数有关,而且往往不是唯一的。 但不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
平均数、中位数和众数都是描述数据集中趋势的统计量
议一议
平均数、中位数和众数有哪些特征?
谈谈学习本节课有什么体会与收获?
学习本节课内容后,你在今后的生活中对待一 些事情进行分析时,对你会有什么帮助?
必做 :作业本
选做:请统计班级里每位同学期望的数学回家作业时间,求出平均数、中位数和众数,根据你所统计的数据及分析结果,向数学老师提交一份建议书。
附表:
作业时间
10分
15分
20分
30分
40分
40分以上
人数(人)
1、下面数据的中位数和众数各是多少?
8,10,10,13,13,13,14,15,17,18,19
3,3,2,3,5,3,10,3
1,4,3,2,4,5
3, 7, 9, 2, 4, 6, 2
2,3,-1,2,1,3,0
众数
中位数
数据
2
2,3
3.5
4
3
3
4
2
在导学案上完成基础练习
1,求下列各组数据的中位数和众数:
-1 , 0 , 1 , 2 , 2 , 3 , 3
9 , 7 , 6 , 4 , 3 , 2 , 2
1 , 2 , 3 , 4 , 4 , 5
10 , 5 , 3 , 3 , 3 , 3 , 3 , 2
排序:
排序:
排序:
排序:
议一议:通过这个练习你能说说中位数和众数的特性吗?
20
20
21
3
20
20
5
练一练
20和35
数 据
中位数
众数
15,20,20,22,35
?
?
-100,20,20,22,1000
?
?
15,20,20,22,35,38
?
?
15,20,20,22,35,35
?
?
-3,0,1,5,5,3,14
?
?
21
20
特性:
4、众数是一组数据中出现次数最多的数据,一定 是这组数据中的某个数据,单位与数据的单位相同。
5、一组数据中的众数有时不只一个,如数据2、 3、-1、2、1、3中,2和3都出现了2次,它们都是这组数据的众数。
1、中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是。
2、求中位数时要将一组数据按大小顺序排列,若这组数据是奇数个,则最中间的数据是中位数,若这组数据是偶数个,则最中间的两个数的平均数是中位数。
3、中位数的单位与数据单位相同。
1、在歌手大奖赛中,去掉一个最高分和一个最低分,将剩下的分数的平均数作为这位歌手的最后得分,为什么?
2、如果在一次考试中,全班同学的成绩的中位数是75分,你恰好得了75分,你知道自己的成绩在全班的位置吗?如果全班同学的成绩的平均分是75分呢?
3、在公园做游戏的一群人的年龄分别为4,5,5,5,4,5,5,6,28,50这组数据的众数为多少?平均数为多少?哪个更有代表性?
平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动,容易受极端值的影响;
中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量,但出现多个众数时,就没多大意义了;
平均数、中位数及众数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。
平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动,容易受极端值的影响;
中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量,但出现多个众数时,就没多大意义了;
平均数、中位数及众数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。
补充练习: 在一次中学生田径运动会上,
参加男子跳高的17名运动员的成绩如下表所示:
成绩(米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的中位数与众数。
2,某班50名学生中,13岁6人,14岁的25人,
15岁的16人,16岁的3人。那么,这个班同
学年龄的众数和中位数分别是( )
A,13,16 B,14,11 C,14,14 D,14,16
C
3人
16人
25人
6人
出现次数
16岁
15岁
14岁
13岁
数据
排序:
13,…,13, 14,…,14, 15,…,15, 16,…,16
6个
25个
16个
3个
第25和第26个数据
红星电子配件厂第一生产组有7名工人,每人的日均生产零件个数是:11,7,13,19,13,13,15
求这组数据的平均数、中位数和众数。
当一组数据中没有特别大或特别小的数据出现时,这组数据的平均数、中位数和众数会非常接近。
1、小明的期中考试成绩(单位 :分)
78,87,96,78,80,95,75
求这一组数据的中位数是 ,
众数是 。
完成导学案上面“当堂检测1,2”
80分
78分
中位数——排序 取中间
众 数——出现次数最多
2,某班50名学生中,13岁6人,14岁的25人,
15岁的16人,16岁的3人。那么,这个班同
学年龄的众数和中位数分别是( )
A,13,16 B,14,11 C,14,14 D,14,16
C
3人
16人
25人
6人
出现次数
16岁
15岁
14岁
13岁
数据
排序:
13,…,13, 14,…,14, 15,…,15, 16,…,16
6个
25个
16个
3个
第25和第26个数据
3、一组数据23,27,20,18, ,12.
它的中位数是21,求x的值。
排序:12, 18, 20, 23, 27
X,
X,
完成导学案上面“当堂检测3,4”
4、当5个整数从小到大排列,其中位数
是4,如果这组数据的唯一众数是6,
则5个整数可能的最大的和是( )
A、21 B、22
C、23 D、24
A
红星电子配件厂第一生产组有7名工人,每人的日均生产零件个数是:11,7,13,19,13,13,15
求这组数据的平均数、中位数和众数。
当一组数据中没有特别大或特别小的数据出现时,这组数据的平均数、中位数和众数会非常接近。
1
3
7
11
5
2
1
数量/双
25
24.5
24
23.5
23
22.5
22
尺码/厘米
某商店销售一批女鞋 30 双,其中各种尺码的
销售量如下表:(单位:双)
(1)计算30双女鞋尺码的平均数、中位数和众数。
(2)在(1)中所求的三个数据中,你认为鞋店老板
最感兴趣的是哪一个?说说你的理由。
做一做
13,
求下列各组数据的中位数
2
15,
19,
23,
5,
12,15,30,18,30
40,35,62,40,99,62
1,2,3,4,5,6,7
求下列各组数据的众数
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
