北师大版八年级数学上册7.3平行线的判定 (1)课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学上册7.3平行线的判定 (1)课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 973.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 20:30:00 | ||
图片预览





文档简介
同角的补角相等
∵∠1+ ∠2=180 °
∠1+ ∠3=180 °
∴ ∠ 2=∠3(同角的补角相等)
等角的补角相等
∵∠1+ ∠2=180 °
∠4+ ∠3=180 °
∠ 1=∠4
∴ ∠ 2=∠3(等角的补角相等)
同角的余角相等
∵∠1+ ∠2=90 °
∠1+ ∠3=90 °
∴ ∠ 2=∠3(同角的余角相等)
等角的余角相等
∵∠1+ ∠2=90 °
∠4+ ∠3=90 °
∠ 1=∠4
∴ ∠ 2=∠3(等角的余角相等)
北师大版八年级上册
平行线的判定
不相交
同位角
内错角
同旁内角
c
a
1
2
b
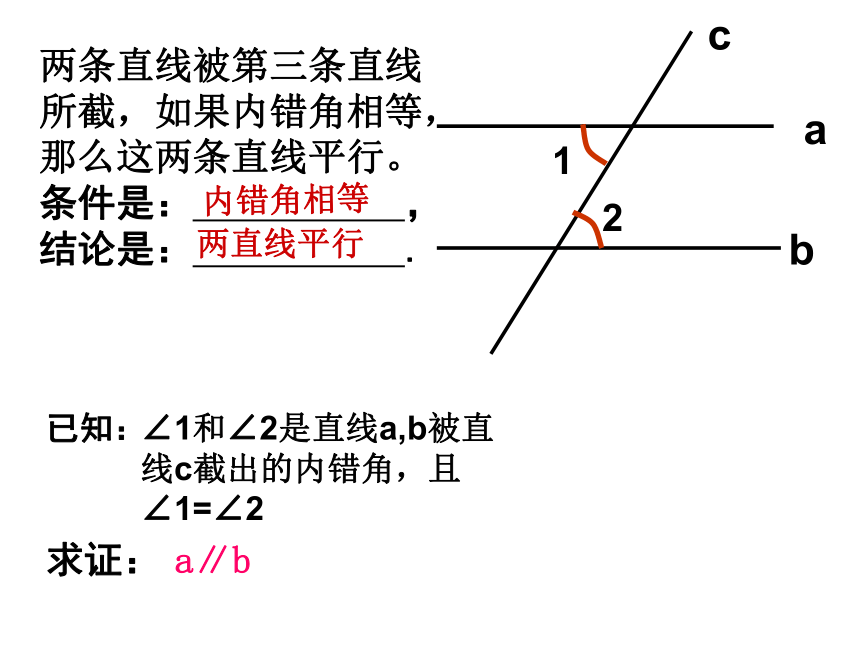
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
条件是: ,结论是: .
内错角相等
两直线平行
∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2
a∥b
已知:
求证:
已知: 如图,∠1和∠2是直线a,b被直线c 截出的内错角,且∠1=∠2.
求证: a∥b.
证明:∵ ∠1=∠2 ,
∠1=∠3 ,
∴∠2=∠3 ,
∴ a∥b .
(已知)
(对顶角的定义)
(等量代换)
(同位角相等,两直线平行)
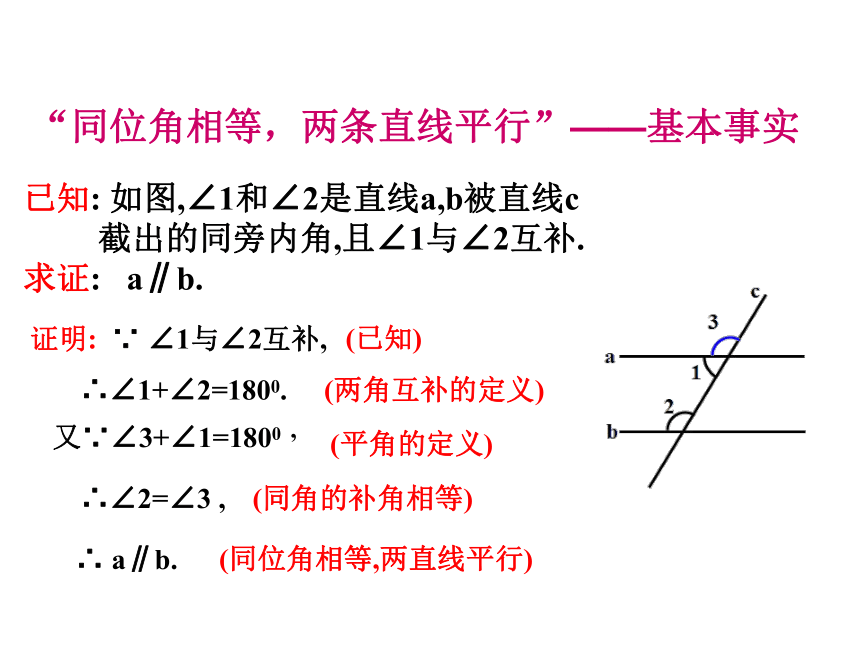
“同位角相等,两条直线平行”——基本事实
c
a
1
2
b
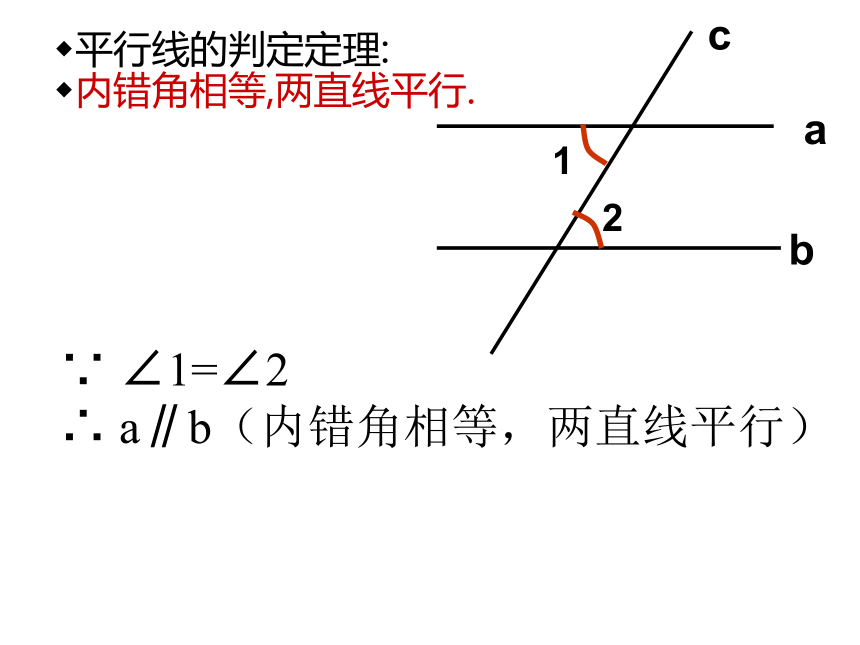
平行线的判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2
∴ a∥b(内错角相等,两直线平行)
c
a
1
b
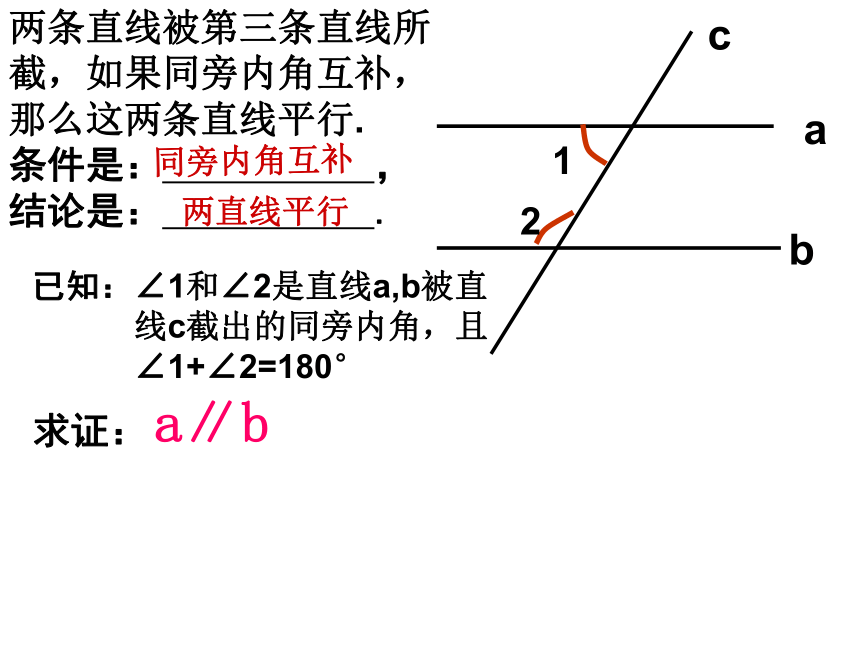
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
条件是: ,结论是: .
同旁内角互补
两直线平行
∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1+∠2=180°
a∥b
已知:
求证:
2
已知: 如图,∠1和∠2是直线a,b被直线c
截出的同旁内角,且∠1与∠2互补.
求证: a∥b.
证明: ∵ ∠1与∠2互补,
∴∠1+∠2=1800.
又∵∠3+∠1=1800 ,
∴∠2=∠3 ,
∴ a∥b.
(已知)
(两角互补的定义)
(平角的定义)
(同角的补角相等)
(同位角相等,两直线平行)
“同位角相等,两条直线平行”——基本事实
c
a
1
b
2
平行线判定定理2:
同旁内角互补,
两直线平行.
∵∠1+∠2=1800
∴ a∥b(同旁内角互补,两直线平行)
公理:
同位角相等,两直线平行.
∵ ∠1=∠2,
∴ a∥b.
判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2,
∴ a∥b.
判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 ,
∴ a∥b.
这里的结论,以后可以直接运用.
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
1.下列推理是否正确?为什么?
(1)如图,∵∠1=∠2,∴
(2)如图,∵∠4+∠5=180°,∴
(3)如图,∵∠2=∠4,∴
(4)如图,∵∠3+∠6=180°,∴
×
√
√
√
2.?如图,∠1=∠2=∠3.填空:
⑴ ∵ ∠1=∠2( )
∴ ∥_____
( )
⑵ ∵∠2=∠3( )
∴ ∥ ( )
已知
AD
BC
BE
CD
已知
同位角相等,两直线平行
内错角相等,两直线平行
例1:已知:如图,直线a,b被直线c所截,
且∠1+∠2=180°.
求证:a∥b
证明:∵ ∠1+∠2=180°(已知)
且∠1+∠3=180°(平角的定义)
∴ ∠2=∠3(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
例2:已知:如图,点D,E分别在AB和AC上,CD平分∠ACB,∠DCB=40°, ∠AED=80°.求证:DE∥BC.
证明:∵ CD平分∠ACB(已知)
∴ ∠ACD=∠BCD= (角平分线定义)
∴ ∠ACB=2 ∠BCD(等式的性质)
∵ ∠DCB=40°(已知)
∴ ∠ACB=80°(等量代换)
∵ ∠AED=80°(已知)
∴ ∠ACB=∠AED(等量代换)
∴DE∥BC(同位角相等,两直线平行)
1.小明用下面的方法做出平行线,你认为他的作法对吗?为什么?
2.蜂房的底部由三个全等的四边形围成,每个四边形的形状如右图所示,其中∠α=109°28′,∠β=70°32′,试确定这三个四边形的对边的位置关系,并说明你的理由.
答:小明的做法对,因为内错角相等,两直线平行
答:这三个四边形的对边分别平行,因为∠α+∠β=180°,同旁内角互补,两直线平行。
3.已知:如图∠1=∠2,∠3=1000,∠B=800.
求证:EF∥DC
证明:∵ ∠1=∠2(已知)
∴CD∥AB(内错角相等,两直线平行)
∵ ∠3=100°,∠B=80°(已知)
∴ ∠3+∠B=100°+80°=180°
(等式的性质)
∴EF∥AB(同旁内角互补,两直线平行)
∴EF∥CD
(平行于同一条直线的两条直线平行 )
4、已知AB⊥AD,CD⊥AD, ∠1=∠2,完成下列推理过程:
证明:∵ AB⊥AD,CD⊥AD(已知)
∴ = =90°( )
又∵ ∠1=∠2(已知)
∴∠BAD-∠1=∠CDA- ( )
即:∠DAE=∠ADF
∴DF∥ ( )
∠1
∠2
∠2
AE
垂直的定义
内错角相等,两直线平行
等式的性质
4、如图,∠DAB被AC平分,且∠1=∠3.
求证:AB∥CD.
2
3
1
C
A
B
D
证明: ∵ AC平分∠DAB (已知)
∴ ∠1=∠2 (角平分线定义)
∵ ∠1=∠3 (已知)
∴ ∠2=∠3 (等量代换)
∴ AB∥CD
(内错角相等,两直线平行)
A
B
C
D
E
F
AB⊥EF,CD⊥EF
AB∥ CD
垂直于同一条直线的两条直线互相平行
∵
∴
在同一平面内,
5.已知直线 AB、CD被EF所截
(如图) ,
判断 AB与CD是否平行,并说
明理由.
AB⊥EF
CD⊥EF
A
B
C
D
E
F
1
2
课内练习
课本P174数学理解---2、3
课堂小结
公理 同位角相等,两直线平行
两条直线都和第三条直线平行,
则这两条直线互相平行
平行线的判定方法
定理 内错角相等,两直线平行
定理 同旁内角互补,两直线平行
c
b
a
∵ ∠1=∠2,
∴ a∥b.
∵ ∠1=∠2,
∴ a∥b.
∵ ∠1+∠2=180°,
∴ a∥b.
a
b
c
a
b
c
a
b
c
∵ a ∥b, a ∥c
∴ b∥c
2
2
2
1
1
1
∵∠1+ ∠2=180 °
∠1+ ∠3=180 °
∴ ∠ 2=∠3(同角的补角相等)
等角的补角相等
∵∠1+ ∠2=180 °
∠4+ ∠3=180 °
∠ 1=∠4
∴ ∠ 2=∠3(等角的补角相等)
同角的余角相等
∵∠1+ ∠2=90 °
∠1+ ∠3=90 °
∴ ∠ 2=∠3(同角的余角相等)
等角的余角相等
∵∠1+ ∠2=90 °
∠4+ ∠3=90 °
∠ 1=∠4
∴ ∠ 2=∠3(等角的余角相等)
北师大版八年级上册
平行线的判定
不相交
同位角
内错角
同旁内角
c
a
1
2
b
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
条件是: ,结论是: .
内错角相等
两直线平行
∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2
a∥b
已知:
求证:
已知: 如图,∠1和∠2是直线a,b被直线c 截出的内错角,且∠1=∠2.
求证: a∥b.
证明:∵ ∠1=∠2 ,
∠1=∠3 ,
∴∠2=∠3 ,
∴ a∥b .
(已知)
(对顶角的定义)
(等量代换)
(同位角相等,两直线平行)
“同位角相等,两条直线平行”——基本事实
c
a
1
2
b
平行线的判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2
∴ a∥b(内错角相等,两直线平行)
c
a
1
b
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
条件是: ,结论是: .
同旁内角互补
两直线平行
∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1+∠2=180°
a∥b
已知:
求证:
2
已知: 如图,∠1和∠2是直线a,b被直线c
截出的同旁内角,且∠1与∠2互补.
求证: a∥b.
证明: ∵ ∠1与∠2互补,
∴∠1+∠2=1800.
又∵∠3+∠1=1800 ,
∴∠2=∠3 ,
∴ a∥b.
(已知)
(两角互补的定义)
(平角的定义)
(同角的补角相等)
(同位角相等,两直线平行)
“同位角相等,两条直线平行”——基本事实
c
a
1
b
2
平行线判定定理2:
同旁内角互补,
两直线平行.
∵∠1+∠2=1800
∴ a∥b(同旁内角互补,两直线平行)
公理:
同位角相等,两直线平行.
∵ ∠1=∠2,
∴ a∥b.
判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2,
∴ a∥b.
判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 ,
∴ a∥b.
这里的结论,以后可以直接运用.
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
1.下列推理是否正确?为什么?
(1)如图,∵∠1=∠2,∴
(2)如图,∵∠4+∠5=180°,∴
(3)如图,∵∠2=∠4,∴
(4)如图,∵∠3+∠6=180°,∴
×
√
√
√
2.?如图,∠1=∠2=∠3.填空:
⑴ ∵ ∠1=∠2( )
∴ ∥_____
( )
⑵ ∵∠2=∠3( )
∴ ∥ ( )
已知
AD
BC
BE
CD
已知
同位角相等,两直线平行
内错角相等,两直线平行
例1:已知:如图,直线a,b被直线c所截,
且∠1+∠2=180°.
求证:a∥b
证明:∵ ∠1+∠2=180°(已知)
且∠1+∠3=180°(平角的定义)
∴ ∠2=∠3(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
例2:已知:如图,点D,E分别在AB和AC上,CD平分∠ACB,∠DCB=40°, ∠AED=80°.求证:DE∥BC.
证明:∵ CD平分∠ACB(已知)
∴ ∠ACD=∠BCD= (角平分线定义)
∴ ∠ACB=2 ∠BCD(等式的性质)
∵ ∠DCB=40°(已知)
∴ ∠ACB=80°(等量代换)
∵ ∠AED=80°(已知)
∴ ∠ACB=∠AED(等量代换)
∴DE∥BC(同位角相等,两直线平行)
1.小明用下面的方法做出平行线,你认为他的作法对吗?为什么?
2.蜂房的底部由三个全等的四边形围成,每个四边形的形状如右图所示,其中∠α=109°28′,∠β=70°32′,试确定这三个四边形的对边的位置关系,并说明你的理由.
答:小明的做法对,因为内错角相等,两直线平行
答:这三个四边形的对边分别平行,因为∠α+∠β=180°,同旁内角互补,两直线平行。
3.已知:如图∠1=∠2,∠3=1000,∠B=800.
求证:EF∥DC
证明:∵ ∠1=∠2(已知)
∴CD∥AB(内错角相等,两直线平行)
∵ ∠3=100°,∠B=80°(已知)
∴ ∠3+∠B=100°+80°=180°
(等式的性质)
∴EF∥AB(同旁内角互补,两直线平行)
∴EF∥CD
(平行于同一条直线的两条直线平行 )
4、已知AB⊥AD,CD⊥AD, ∠1=∠2,完成下列推理过程:
证明:∵ AB⊥AD,CD⊥AD(已知)
∴ = =90°( )
又∵ ∠1=∠2(已知)
∴∠BAD-∠1=∠CDA- ( )
即:∠DAE=∠ADF
∴DF∥ ( )
∠1
∠2
∠2
AE
垂直的定义
内错角相等,两直线平行
等式的性质
4、如图,∠DAB被AC平分,且∠1=∠3.
求证:AB∥CD.
2
3
1
C
A
B
D
证明: ∵ AC平分∠DAB (已知)
∴ ∠1=∠2 (角平分线定义)
∵ ∠1=∠3 (已知)
∴ ∠2=∠3 (等量代换)
∴ AB∥CD
(内错角相等,两直线平行)
A
B
C
D
E
F
AB⊥EF,CD⊥EF
AB∥ CD
垂直于同一条直线的两条直线互相平行
∵
∴
在同一平面内,
5.已知直线 AB、CD被EF所截
(如图) ,
判断 AB与CD是否平行,并说
明理由.
AB⊥EF
CD⊥EF
A
B
C
D
E
F
1
2
课内练习
课本P174数学理解---2、3
课堂小结
公理 同位角相等,两直线平行
两条直线都和第三条直线平行,
则这两条直线互相平行
平行线的判定方法
定理 内错角相等,两直线平行
定理 同旁内角互补,两直线平行
c
b
a
∵ ∠1=∠2,
∴ a∥b.
∵ ∠1=∠2,
∴ a∥b.
∵ ∠1+∠2=180°,
∴ a∥b.
a
b
c
a
b
c
a
b
c
∵ a ∥b, a ∥c
∴ b∥c
2
2
2
1
1
1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
