北师大版九年级数学下册 3.1 圆 课件 (共21张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 3.1 圆 课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:00:00 | ||
图片预览







文档简介
北师大版九年级下册 第三章 圆
§3.1 圆
那车轮为什么做成圆形?
探究一:情景1
450
一些学生正在做投圈游戏,他们投圈的目标都是图中的花瓶,如果他们呈“一”字排开,这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形?
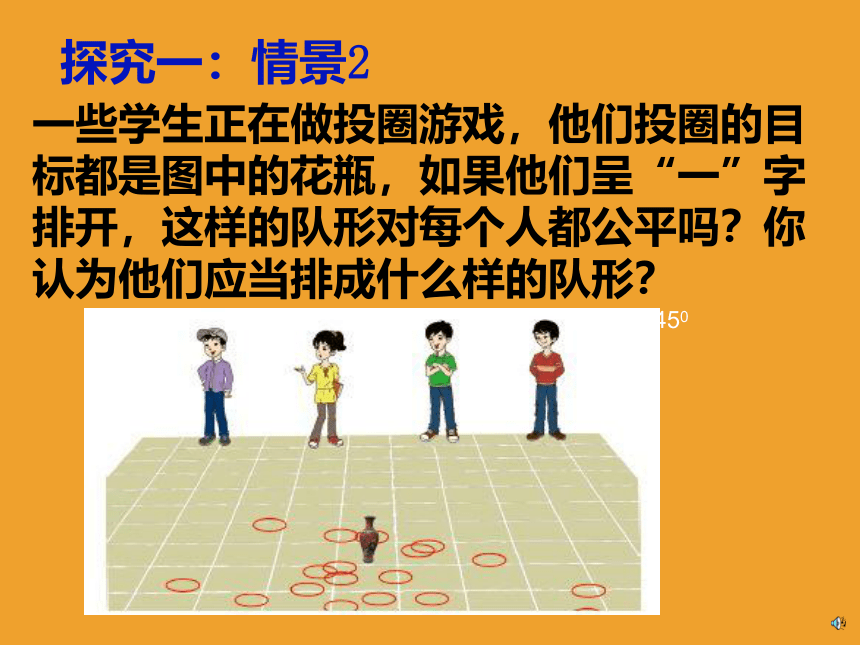
探究一:情景2
通过刚才的两个情
景,我们发现轴心
和花瓶是一个固定
的点,轮胎上的点
和游戏者到定点的
距离等于定长,如
此,圆又有了一个
全新的定义!
解: (1)sin300+cos450
思考
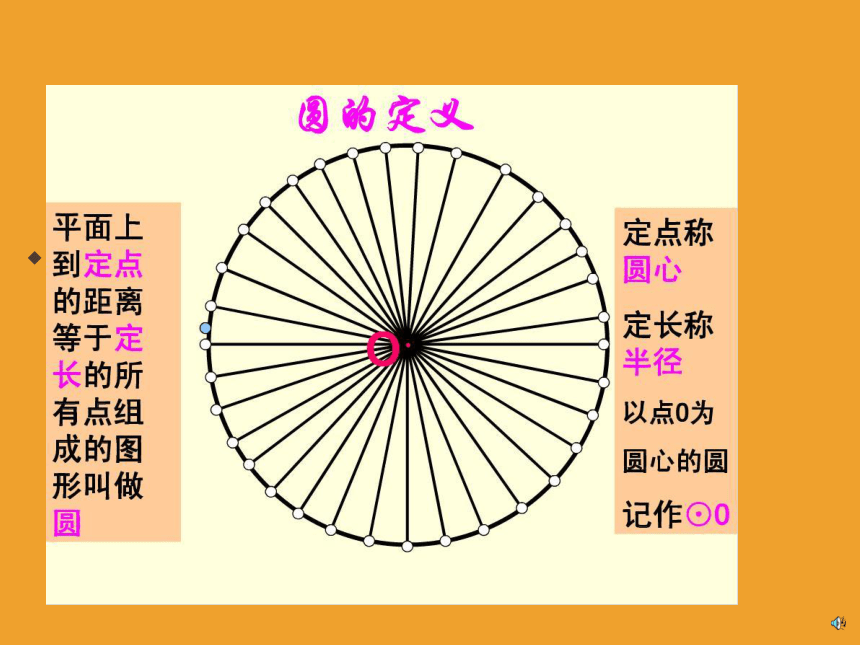
要画一个圆,需要确定它的哪些要素?
圆心
半径
圆的相关概念以及之间关系
1、弦和直径:
连接圆上任意两点的线段叫做弦;经过圆心的弦叫做直径。
2、弧和半圆(其中包括优弧和劣弧):
圆上任意两点间的部分叫做圆弧;圆的任意一条直径的两个
端点分圆成两条弧,每一条弧都叫做半圆。
思考1:弦和直径有什么关系?
直径是弦,但弦不一定是直径。
思考2:半圆和弧有什么关系?
半圆一定是弧,但弧不一定是半圆。
思考3:等弧的长度相等吗?长度相等的弧是等弧吗?
等弧的长度一定相等,但长度相等的弧不一定
是等弧。
圆的相关概念以及之间关系
3、等圆和等弧:
能够重合的两个圆叫做等圆;在同圆或等圆中,能够互相重
合的弧叫做等弧。
1.一个圆的最大弦长是12cm,则该圆的面积为 。
2.下列说法正确的是( )
A.弦是直径 B.长度相等的弧是等弧
C.半圆是弧 D.过圆心的线段是直径
3.下列说法正确的有( )个。
(1)大于半圆的弧叫优弧,小于半圆的弧叫劣弧(2)优弧一定比劣弧长(3)任意一条弦都把圆周分成两条弧,一条优弧,一条劣弧.
A.0 B.1 C.2 D.3
36π
C
B
跟踪练习一:
放寒假了,爱好运动的小明和小颖相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离中心越近,谁就胜.如图①中就是他们两人掷镖的落点.我们不妨取其中的一个圆和飞镖的落点来研究,如图② :
探究二:
图①
图②
(1)这些点相对于圆的位置有哪些情况?
探究二:
(2)知道一个点和圆的位置关系,点到圆心的距离d和半径r的关系是什么?
探究二:
点在圆外 d > r ;
点在圆上 d = r ;
点在圆内 d < r ;
?
?
?
点与圆的位置关系(其中点到圆心的距离为d):
跟踪练习二:
⊙O的直径为6,点A到圆心O的距离OA=3,则点A与⊙O的位置关系是 .
已知⊙O的面积为25π,判断点P与
⊙O的位置关系.
(1)若PO=5.5,则点P在( )
(2)若PO= 4,则点P在 ;
(3)若PO= ,则点P在圆上.
点A在圆上
圆O外
圆O内
5
挑战自我:
3. 设AB=3厘米,作图说明满足下列要求的图形:
(1)到点A和点B的距离都等于2厘米的所有点组成的图形.
A
B
挑战自我:
(2)和点A、B的距离都小于2厘米的所有点组成的图形.
通过本节课的学习,你有哪些收获?
1. 下列说法错误的是( )
A.直径是弦 B.长度相等的弧是等弧
C.半径相等的圆是等圆 D.圆上两点之间的部分为弧?
2.在矩形ABCD中,AB=3cm,AD=4cm,以C为圆心,4cm长为半径做圆,则A、B、C、D四点中,在圆内的有( )
A.4 B.3个 C.2个 D.1个
B
C
达标检测:
3.已知⊙O的周长为8πcm,
若PO=2cm,则点P在( );
若PO= 4cm,则点P在( );
若PO=6cm,则点P( ).
4.点A的坐标(3,0),点B的坐标为(0,4)则点B在以A为圆心,4为半径的( )
圆O内
圆O上
圆O外
圆外
达标检测:
5.设AB=5厘米,作图说明满足下列要求的图形:
(1)到点A、B的距离都小于3厘米的所有点组成的图形.
(2)到点A的距离小于3厘米,到点B的距离大于3厘米所有点组成的图形.
?
?
达标检测:
布置作业:
A类:习题3.1;
B类:习题3.1,新课堂本课时.
谢谢聆听!
§3.1 圆
那车轮为什么做成圆形?
探究一:情景1
450
一些学生正在做投圈游戏,他们投圈的目标都是图中的花瓶,如果他们呈“一”字排开,这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形?
探究一:情景2
通过刚才的两个情
景,我们发现轴心
和花瓶是一个固定
的点,轮胎上的点
和游戏者到定点的
距离等于定长,如
此,圆又有了一个
全新的定义!
解: (1)sin300+cos450
思考
要画一个圆,需要确定它的哪些要素?
圆心
半径
圆的相关概念以及之间关系
1、弦和直径:
连接圆上任意两点的线段叫做弦;经过圆心的弦叫做直径。
2、弧和半圆(其中包括优弧和劣弧):
圆上任意两点间的部分叫做圆弧;圆的任意一条直径的两个
端点分圆成两条弧,每一条弧都叫做半圆。
思考1:弦和直径有什么关系?
直径是弦,但弦不一定是直径。
思考2:半圆和弧有什么关系?
半圆一定是弧,但弧不一定是半圆。
思考3:等弧的长度相等吗?长度相等的弧是等弧吗?
等弧的长度一定相等,但长度相等的弧不一定
是等弧。
圆的相关概念以及之间关系
3、等圆和等弧:
能够重合的两个圆叫做等圆;在同圆或等圆中,能够互相重
合的弧叫做等弧。
1.一个圆的最大弦长是12cm,则该圆的面积为 。
2.下列说法正确的是( )
A.弦是直径 B.长度相等的弧是等弧
C.半圆是弧 D.过圆心的线段是直径
3.下列说法正确的有( )个。
(1)大于半圆的弧叫优弧,小于半圆的弧叫劣弧(2)优弧一定比劣弧长(3)任意一条弦都把圆周分成两条弧,一条优弧,一条劣弧.
A.0 B.1 C.2 D.3
36π
C
B
跟踪练习一:
放寒假了,爱好运动的小明和小颖相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离中心越近,谁就胜.如图①中就是他们两人掷镖的落点.我们不妨取其中的一个圆和飞镖的落点来研究,如图② :
探究二:
图①
图②
(1)这些点相对于圆的位置有哪些情况?
探究二:
(2)知道一个点和圆的位置关系,点到圆心的距离d和半径r的关系是什么?
探究二:
点在圆外 d > r ;
点在圆上 d = r ;
点在圆内 d < r ;
?
?
?
点与圆的位置关系(其中点到圆心的距离为d):
跟踪练习二:
⊙O的直径为6,点A到圆心O的距离OA=3,则点A与⊙O的位置关系是 .
已知⊙O的面积为25π,判断点P与
⊙O的位置关系.
(1)若PO=5.5,则点P在( )
(2)若PO= 4,则点P在 ;
(3)若PO= ,则点P在圆上.
点A在圆上
圆O外
圆O内
5
挑战自我:
3. 设AB=3厘米,作图说明满足下列要求的图形:
(1)到点A和点B的距离都等于2厘米的所有点组成的图形.
A
B
挑战自我:
(2)和点A、B的距离都小于2厘米的所有点组成的图形.
通过本节课的学习,你有哪些收获?
1. 下列说法错误的是( )
A.直径是弦 B.长度相等的弧是等弧
C.半径相等的圆是等圆 D.圆上两点之间的部分为弧?
2.在矩形ABCD中,AB=3cm,AD=4cm,以C为圆心,4cm长为半径做圆,则A、B、C、D四点中,在圆内的有( )
A.4 B.3个 C.2个 D.1个
B
C
达标检测:
3.已知⊙O的周长为8πcm,
若PO=2cm,则点P在( );
若PO= 4cm,则点P在( );
若PO=6cm,则点P( ).
4.点A的坐标(3,0),点B的坐标为(0,4)则点B在以A为圆心,4为半径的( )
圆O内
圆O上
圆O外
圆外
达标检测:
5.设AB=5厘米,作图说明满足下列要求的图形:
(1)到点A、B的距离都小于3厘米的所有点组成的图形.
(2)到点A的距离小于3厘米,到点B的距离大于3厘米所有点组成的图形.
?
?
达标检测:
布置作业:
A类:习题3.1;
B类:习题3.1,新课堂本课时.
谢谢聆听!
