北师大版九年级数学下册 1.1 锐角三角函数 (4)(共19张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 1.1 锐角三角函数 (4)(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 670.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:00:00 | ||
图片预览



文档简介
北师大版九年级下册第一章
源于生活的数学
从梯子的倾斜程度谈起
梯子是我们日常生活中常见的物体
你能比较两个梯子哪个更陡吗?你有哪些办法?
在实践中探索
小丽的问题,如图:
梯子AB和EF哪个更陡?你是怎样判断的?
?
2m
2m
6m
5m
A
B
C
D
E
F
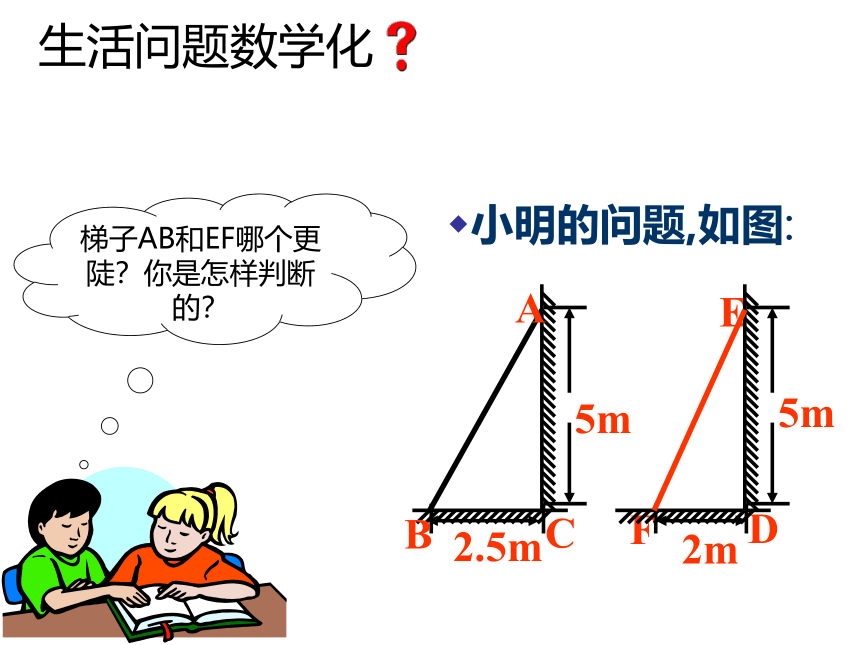
生活问题数学化
小明的问题,如图:
梯子AB和EF哪个更陡?你是怎样判断的?
5m
2.5m
C
B
A
2m
E
5m
D
F
小亮的问题,如图:
梯子AB和EF哪个更陡?你是怎样判断的?
3m
2m
6m
4m
A
B
C
D
E
F
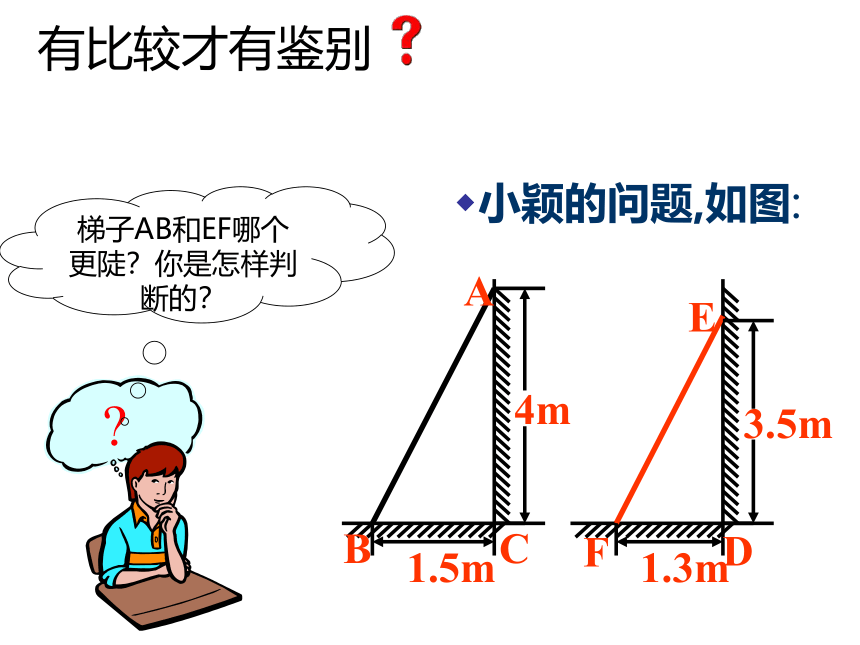
有比较才有鉴别
小颖的问题,如图:
?
梯子AB和EF哪个更陡?你是怎样判断的?
1.5m
A
4m
C
B
1.3m
E
3.5m
D
F
想一想
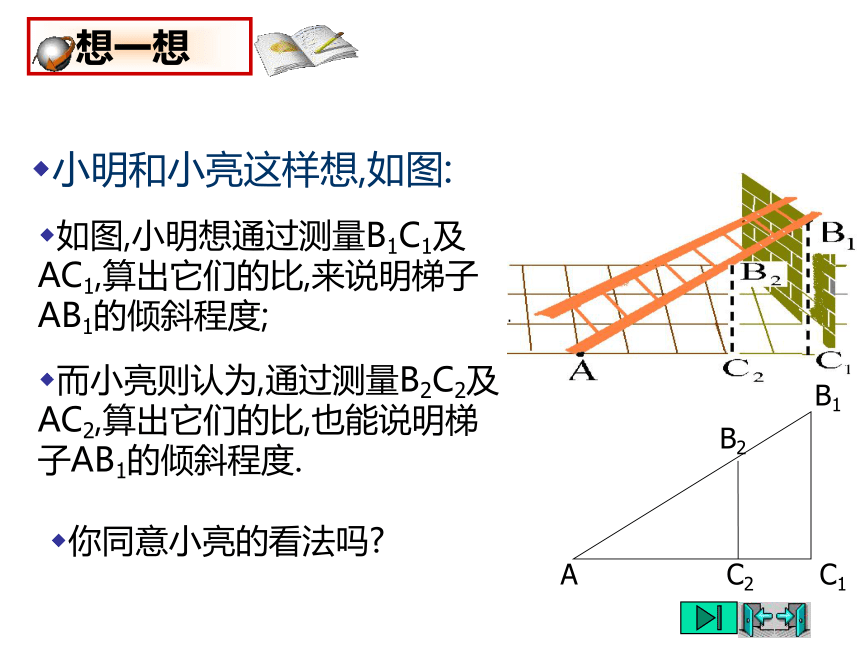
小明和小亮这样想,如图:
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.
你同意小亮的看法吗?
A
B1
C2
C1
B2
由感性到理性
直角三角形的边与角的关系
(1).Rt△AB1C1和Rt△AB2C2有什么关系?
如果改变B2在梯子上的位置(如B3C3 )呢?
由此你得出什么结论?
驶向胜利的彼岸
A
B1
C2
C1
B2
C3
B3
直角三角形中边与角的关系:锐角的三角函数--正切函数
驶向胜利的彼岸
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
在Rt△ABC中,如果锐角A确定,那么它的对边与邻边的比随之确定,这个比叫做∠A的正切,记作tanA,即
定义中应该注意的几个问题:
拓展
1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;对于三个大写字母或者数字表示的角则不能省略角的符号.
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.
八仙过海,尽显才能
如图,梯子AB1的倾斜程度与tanA有关吗?
与∠A有关吗?
议一议
与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.
A
B1
C2
C1
B2
例1 下图表示两个自动扶梯,那一个自动扶梯比较陡?
例题欣赏
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
老师提示:
生活中,常用一个锐角的正切表示梯子的倾斜程度.
用数学去解释生活
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
老师提示:
坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.
100m
60m
┌
α
i
1.鉴宝专家—--是真是假:
随堂练习P6
15
老师期望:你能从中悟出点东西.
驶向胜利的彼岸
(1).如图 (1)
( ).
A
B
C
┍
A
B
C
7m
10m
(1)
(2)
(2).如图 (2)
( ).
(3).如图 (2)
( ).
(4).如图 (2)
( ).
(5).如图 (2)
( ).
(6).如图 (2)
( ).
A
7
.
0
tan
=
2.如图, ∠C=90°,CD⊥AB.
随堂练习P6
17
3.在上图中,若BD=6,CD=12.求tanA的值.
老师提示:
模型“双垂直三角形”的有关性质你可曾记得.
┍
┌
A
C
B
D
( ) ( )
( ) ( )
.
tan
=
=
B
回味无穷
回顾,反思,深化
小结 拓展
1.正切的定义:
驶向胜利的彼岸
A
B
C
∠A的对边
∠A的邻边
┌
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA=
1.如图,分别根据图(1)和图(2)求tanA的值.
课堂检测
2.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC和AB.
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
A
C
B
3
4
┌
A
C
B
3
4
(1)
(2)
3.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.
4.在等腰△ABC,AB=AC=13,BC=10,求tanB.
老师提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
结束寄语
数学中的某些定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏极深.
——高斯
下课了!
源于生活的数学
从梯子的倾斜程度谈起
梯子是我们日常生活中常见的物体
你能比较两个梯子哪个更陡吗?你有哪些办法?
在实践中探索
小丽的问题,如图:
梯子AB和EF哪个更陡?你是怎样判断的?
?
2m
2m
6m
5m
A
B
C
D
E
F
生活问题数学化
小明的问题,如图:
梯子AB和EF哪个更陡?你是怎样判断的?
5m
2.5m
C
B
A
2m
E
5m
D
F
小亮的问题,如图:
梯子AB和EF哪个更陡?你是怎样判断的?
3m
2m
6m
4m
A
B
C
D
E
F
有比较才有鉴别
小颖的问题,如图:
?
梯子AB和EF哪个更陡?你是怎样判断的?
1.5m
A
4m
C
B
1.3m
E
3.5m
D
F
想一想
小明和小亮这样想,如图:
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.
你同意小亮的看法吗?
A
B1
C2
C1
B2
由感性到理性
直角三角形的边与角的关系
(1).Rt△AB1C1和Rt△AB2C2有什么关系?
如果改变B2在梯子上的位置(如B3C3 )呢?
由此你得出什么结论?
驶向胜利的彼岸
A
B1
C2
C1
B2
C3
B3
直角三角形中边与角的关系:锐角的三角函数--正切函数
驶向胜利的彼岸
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
在Rt△ABC中,如果锐角A确定,那么它的对边与邻边的比随之确定,这个比叫做∠A的正切,记作tanA,即
定义中应该注意的几个问题:
拓展
1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;对于三个大写字母或者数字表示的角则不能省略角的符号.
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.
八仙过海,尽显才能
如图,梯子AB1的倾斜程度与tanA有关吗?
与∠A有关吗?
议一议
与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.
A
B1
C2
C1
B2
例1 下图表示两个自动扶梯,那一个自动扶梯比较陡?
例题欣赏
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
老师提示:
生活中,常用一个锐角的正切表示梯子的倾斜程度.
用数学去解释生活
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
老师提示:
坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.
100m
60m
┌
α
i
1.鉴宝专家—--是真是假:
随堂练习P6
15
老师期望:你能从中悟出点东西.
驶向胜利的彼岸
(1).如图 (1)
( ).
A
B
C
┍
A
B
C
7m
10m
(1)
(2)
(2).如图 (2)
( ).
(3).如图 (2)
( ).
(4).如图 (2)
( ).
(5).如图 (2)
( ).
(6).如图 (2)
( ).
A
7
.
0
tan
=
2.如图, ∠C=90°,CD⊥AB.
随堂练习P6
17
3.在上图中,若BD=6,CD=12.求tanA的值.
老师提示:
模型“双垂直三角形”的有关性质你可曾记得.
┍
┌
A
C
B
D
( ) ( )
( ) ( )
.
tan
=
=
B
回味无穷
回顾,反思,深化
小结 拓展
1.正切的定义:
驶向胜利的彼岸
A
B
C
∠A的对边
∠A的邻边
┌
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA=
1.如图,分别根据图(1)和图(2)求tanA的值.
课堂检测
2.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC和AB.
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
A
C
B
3
4
┌
A
C
B
3
4
(1)
(2)
3.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.
4.在等腰△ABC,AB=AC=13,BC=10,求tanB.
老师提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
结束寄语
数学中的某些定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏极深.
——高斯
下课了!
