北师大版九年级数学下册 3.4 圆周角与圆心角的关系 课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 3.4 圆周角与圆心角的关系 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 866.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 22:51:14 | ||
图片预览



文档简介
圆周角与圆心角的关系
知识回顾
1.什么叫圆心角?
.
O
A
B
顶点在圆心的角叫圆心角
B
A
C
D
E
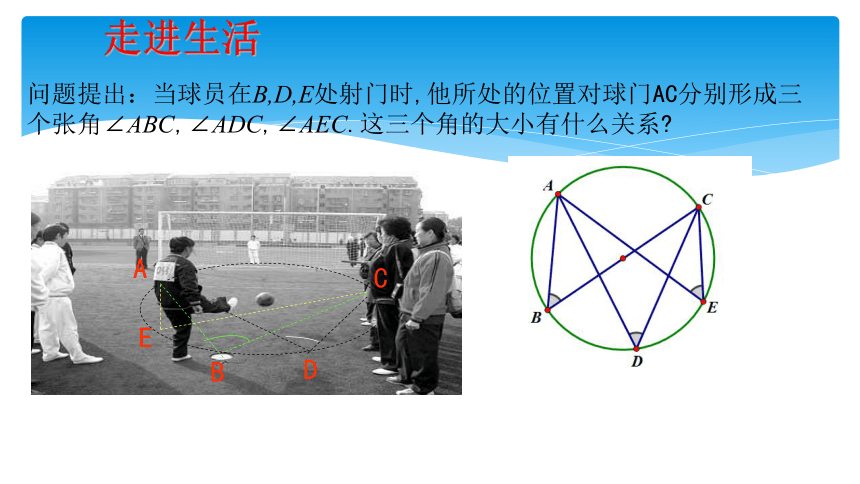
问题提出:当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?
走进生活
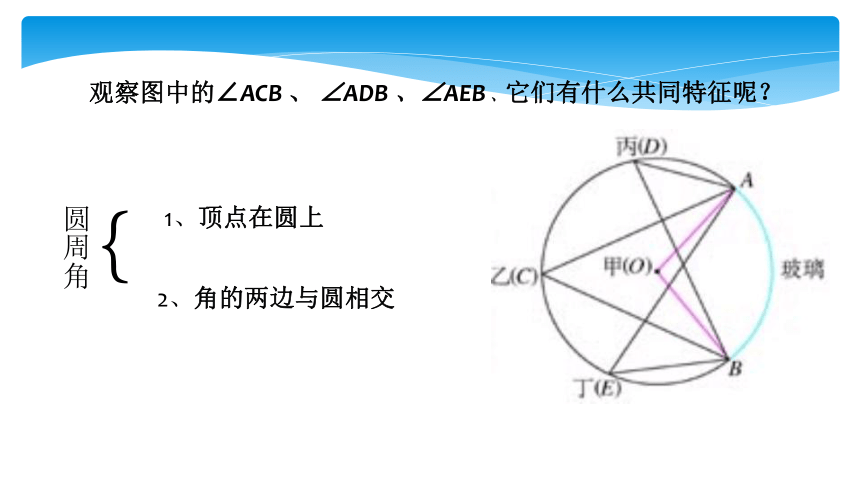
观察图中的∠ACB 、 ∠ADB 、∠AEB 、它们有什么共同特征呢?
1、顶点在圆上
2、角的两边与圆相交
{
圆周角
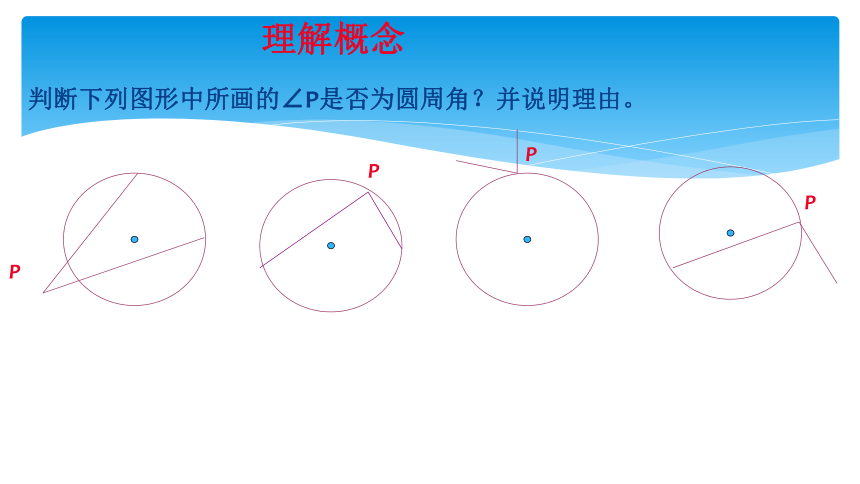
判断下列图形中所画的∠P是否为圆周角?并说明理由。
理解概念
P
P
P
P
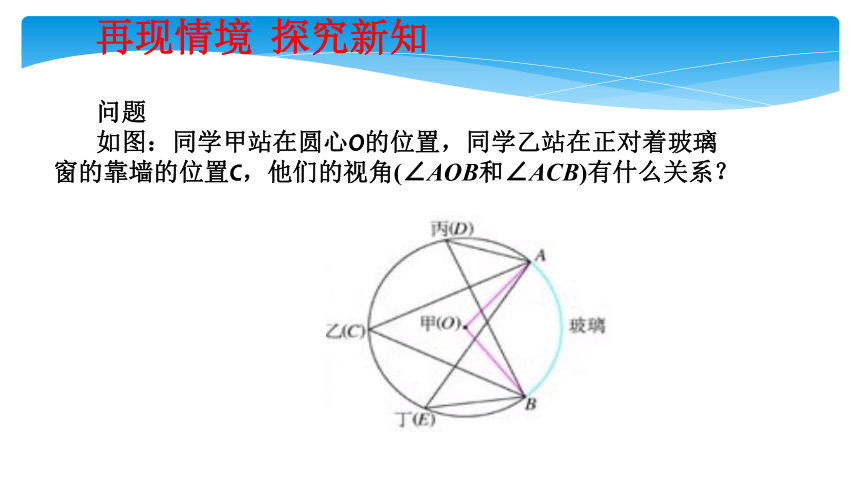
问题
如图:同学甲站在圆心O的位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?
再现情境 探究新知
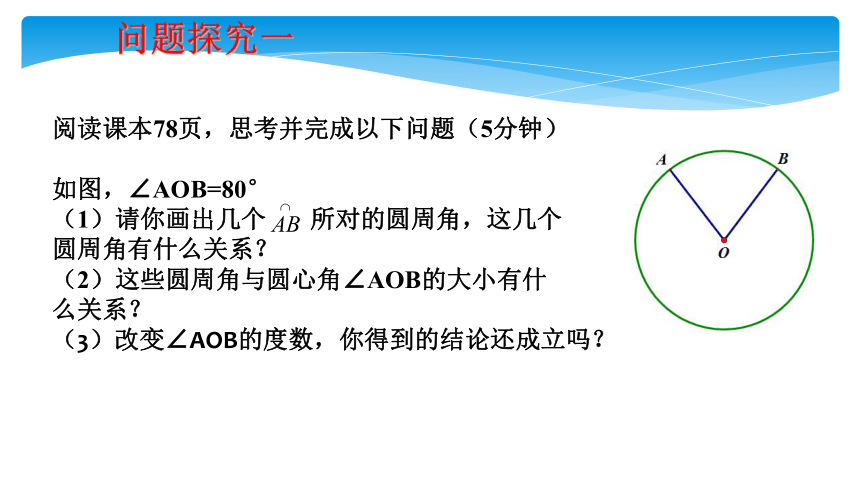
问题探究一
阅读课本78页,思考并完成以下问题(5分钟)
如图,∠AOB=80°
(1)请你画出几个 所对的圆周角,这几个
圆周角有什么关系?
(2)这些圆周角与圆心角∠AOB的大小有什
么关系?
(3)改变∠AOB的度数,你得到的结论还成立吗?
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
∠ADB=∠ACB= ?∠AOB
动手动脑 验证新知
问题1
画一个圆,在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?
问题2
当圆心在圆周角的一边上时,如何证明圆心角与圆周角的关系呢?
问题3
另外两种情况如何证明,可否转化成第一种情况呢?
反馈练习一
1.如图,∠O=50°,求∠A的度数.
2.已知∠BCD=120°,求图中∠AOB的度数.
智者加速:
如图,在直径为AB的圆O中,∠DAB=30°,
∠COD=60°,OD与AC平行吗?为什么?
问题探究二
阅读课本80-82页,思考以下问题(6分钟)
1.在课前射门游戏中,当球员在B、D、E处射门时,
所形成的三个张角∠ABC,∠ADC,∠AEC的大小
有什么关系?你能用圆周角定理证明你的结论吗?
2.(1)如图,BC是圆O 的直径,它所对的圆周角有什么
特点?你能证明你的结论吗?
(2)在图中,圆周角∠A=90°,弦BC是直径吗?为什么?
问题探究二
∠ABC=∠ADC=∠AEC
结论:同弧或等弧所对的圆周角相等.
问题探究二
(1)如图,BC是圆O 的直径,它所对的圆周角有什么
特点?你能证明你的结论吗?
(2)在图中,圆周角∠A=90°,弦BC是直径吗?为什么?
结论:直径所对的圆周角是直角;90°的圆周角所对的弦是直径
随堂练习
小明想用直角尺检查某些工件是否恰好为半圆形。下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
反馈练习二
1.如图,圆O的直径AB=10cm,C为圆O上的一点,∠B=30°,求AC的长.
2.如图,AB是圆O的直径,∠C=15°,求∠BAD的度数.
【链接中考】
如图,BC是圆O 的直径,A是圆O上一点,∠OAC=32°,则∠B的度数是( )
A.58° B.60°C.64° D.68°
盘点知识 提升能力
问题:
通过本节课的学习你有哪些收获?
用直角曲尺检查半圆形的工件
1、如图,在⊙O中,∠ABC=50°,则∠AOC等于( )
A、50°; B、80°;C、90°; D、100°
达标检测
A
C
B
O
2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等( )
A、30°; B、60°;C、90°; D、45°
C
A
B
P
3、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30 °,AB=2,则⊙O的半径是 。
C
A
B
O
1.如图,在圆O中,弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25° B.27.5° C.30° D.35°
2.如图,AB为圆O的直径,CD是圆O 的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
3.如图,AB是圆O的直径,点C,D,E在圆O上,若∠AED=20°,则∠BCD的度数为( )
A.100° B.110° C.115° D.120°
中考链接
知识回顾
1.什么叫圆心角?
.
O
A
B
顶点在圆心的角叫圆心角
B
A
C
D
E
问题提出:当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?
走进生活
观察图中的∠ACB 、 ∠ADB 、∠AEB 、它们有什么共同特征呢?
1、顶点在圆上
2、角的两边与圆相交
{
圆周角
判断下列图形中所画的∠P是否为圆周角?并说明理由。
理解概念
P
P
P
P
问题
如图:同学甲站在圆心O的位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?
再现情境 探究新知
问题探究一
阅读课本78页,思考并完成以下问题(5分钟)
如图,∠AOB=80°
(1)请你画出几个 所对的圆周角,这几个
圆周角有什么关系?
(2)这些圆周角与圆心角∠AOB的大小有什
么关系?
(3)改变∠AOB的度数,你得到的结论还成立吗?
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
∠ADB=∠ACB= ?∠AOB
动手动脑 验证新知
问题1
画一个圆,在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?
问题2
当圆心在圆周角的一边上时,如何证明圆心角与圆周角的关系呢?
问题3
另外两种情况如何证明,可否转化成第一种情况呢?
反馈练习一
1.如图,∠O=50°,求∠A的度数.
2.已知∠BCD=120°,求图中∠AOB的度数.
智者加速:
如图,在直径为AB的圆O中,∠DAB=30°,
∠COD=60°,OD与AC平行吗?为什么?
问题探究二
阅读课本80-82页,思考以下问题(6分钟)
1.在课前射门游戏中,当球员在B、D、E处射门时,
所形成的三个张角∠ABC,∠ADC,∠AEC的大小
有什么关系?你能用圆周角定理证明你的结论吗?
2.(1)如图,BC是圆O 的直径,它所对的圆周角有什么
特点?你能证明你的结论吗?
(2)在图中,圆周角∠A=90°,弦BC是直径吗?为什么?
问题探究二
∠ABC=∠ADC=∠AEC
结论:同弧或等弧所对的圆周角相等.
问题探究二
(1)如图,BC是圆O 的直径,它所对的圆周角有什么
特点?你能证明你的结论吗?
(2)在图中,圆周角∠A=90°,弦BC是直径吗?为什么?
结论:直径所对的圆周角是直角;90°的圆周角所对的弦是直径
随堂练习
小明想用直角尺检查某些工件是否恰好为半圆形。下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
反馈练习二
1.如图,圆O的直径AB=10cm,C为圆O上的一点,∠B=30°,求AC的长.
2.如图,AB是圆O的直径,∠C=15°,求∠BAD的度数.
【链接中考】
如图,BC是圆O 的直径,A是圆O上一点,∠OAC=32°,则∠B的度数是( )
A.58° B.60°C.64° D.68°
盘点知识 提升能力
问题:
通过本节课的学习你有哪些收获?
用直角曲尺检查半圆形的工件
1、如图,在⊙O中,∠ABC=50°,则∠AOC等于( )
A、50°; B、80°;C、90°; D、100°
达标检测
A
C
B
O
2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等( )
A、30°; B、60°;C、90°; D、45°
C
A
B
P
3、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30 °,AB=2,则⊙O的半径是 。
C
A
B
O
1.如图,在圆O中,弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25° B.27.5° C.30° D.35°
2.如图,AB为圆O的直径,CD是圆O 的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
3.如图,AB是圆O的直径,点C,D,E在圆O上,若∠AED=20°,则∠BCD的度数为( )
A.100° B.110° C.115° D.120°
中考链接
