北师大版九年级数学下册:3.4 圆周角和圆心角的关系 课件(共23张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:3.4 圆周角和圆心角的关系 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 22:45:43 | ||
图片预览




文档简介
一条弧所对的圆周角等于它所对的圆心角的一半,实际讲的时候用了2天,注意时间,注意15页的第三题
圆周角和圆心角的关系第1课时
前言
二次函数结束后复习了近一周的时间,开始《圆》这一章,开始的时间为10月15号。整个这章是按北师大教材讲的,很多在人教版教材中涉及的内容都没有讲解,例如切线长\弦切角定理\相交弦定理等等。 2014届教材改版了,新调整的教材顺序很好,就用新教材的顺序了。
时间
10月15号至11月8号,但实际从8号到月末计划一直进行《二次函数》和《圆》的综合复习,这一部分的复习及计划会单独以章节形式出现。至此本部分课件结束。
内容调整1------2010版本
①《圆的对称性》中轴对称和中心对称放到了第一课时,这样在”垂径定理”处可以以一课时讲清垂径定理和后一节则讲清推论及部分应用,第三节则处理圆心角等。②《圆的对称性》这一节,由轴对称出垂径定理;由中心对称出圆心角, 弧,弦,弦心距之间的关系,正好是两路两节。③在同圆或等圆中,相等的弧所对的圆周角有什么关系?这个问题的前提是先探究一条弧所对的圆周角和圆心角之间有的关系?在《圆周角和圆心角的关系》第一课时④外心在《确定圆的条件》,而内心在《直线和圆的位置关系3课时》,注意和上学期《证明三》联系。
内容调整2------2014版本
2014届教材改版了,新调整的教材顺序很好,就用新教材的顺序了。
习题
①有时间就坚持二次函数的A4纸。课上的内容在保证速度的前提下,最好快一点,这样可以有时间去处理《倍速》。资源的习题较少,必须得配合其他练习册。
②《圆的对称性》有一道在圆中利用对称性求最短距离的题,至此正好是四道:1水站2正方形3圆4蚂蚁
③后期复习习题较多,注意保留
4.1 圆
1课时 圆的相关概念+点与圆的位置关系
4.2 圆的对称性
1课时 轴对称和中心对称+圆心角, 弧,弦,弦心距之间的关系
2课时 处理上两节课的习题
4.3 垂径定理
1课时 垂径定理9条,要求记录+推论1
2课时 推论2+垂径定理复习+赵州桥
4.4 圆周角和圆心角的关系
1课时 圆周角和圆心角关系
2课时 圆周角定理的推论1和2
4.5 确定圆的条件
1课时 确定圆的条件和外接圆等等
4.6 直线和圆的位置关系
1课时 直线和圆的位置关系及相应习题
2课时 切线的性质和判定定理
3课时 三角形外接圆和内切圆及直角三角形内切圆半径公式
4.7 切线长定理
1课时
4.8 圆内接正多边形
1课时
4.9 弧长及扇形的面积
1课时 弧长及扇形的面积
课 堂
流 程
新知 我体验
拓展 我提升
反馈 我挑战
感悟 我反思
目标 我清晰
课堂 ★ 流程
知识与技能
过程与方法
情感态度价值
1.了解圆周角的概念。2.理解圆周角定理的证明
经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化来解决一般性问题的方法,渗透分类的数学思想
通过观察、猜想、验证推理,培养学生探索问题的能力和方法
目标 我清晰
新知 我体验
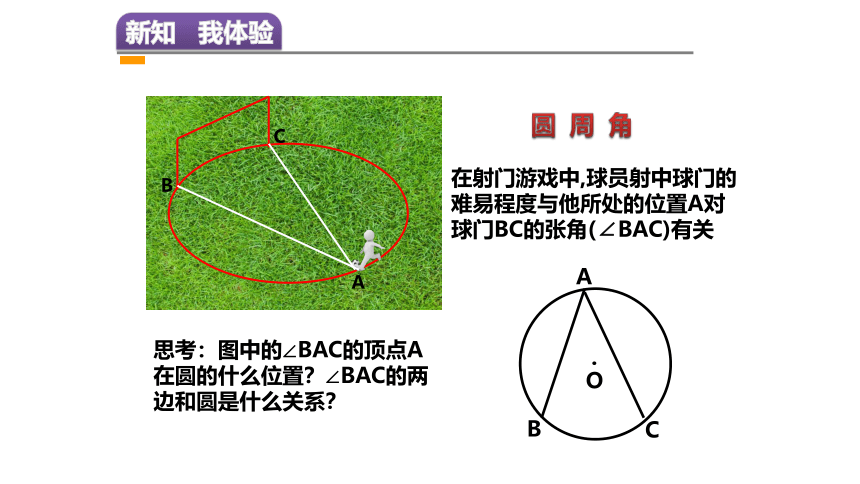
圆周角
在射门游戏中,球员射中球门的难易程度与他所处的位置A对球门BC的张角(∠BAC)有关
A
B
C
.
O
B
C
A
思考:图中的∠BAC的顶点A在圆的什么位置?∠BAC的两边和圆是什么关系?
新知 我体验
.
O
B
C
A
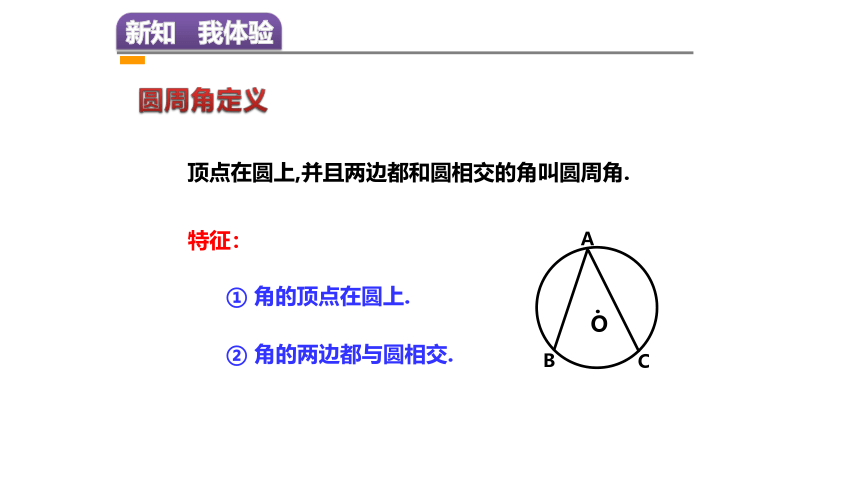
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
圆周角定义
新知 我体验
1 、判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
2 、指出图中的圆周角
∠ACO ∠ACB ∠ BCO ∠OAB ∠BAC ∠OAC ∠ABO ∠CBO ∠ABC
新知 我体验
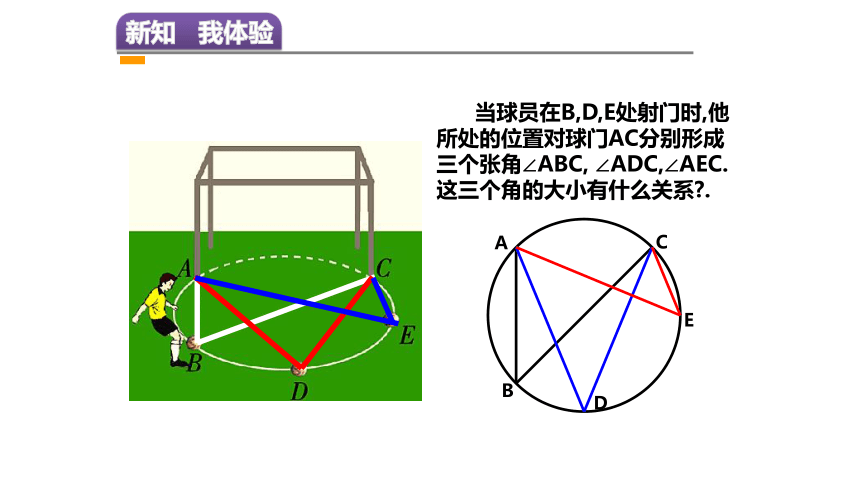
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.
A
B
D
E
C
新知 我体验
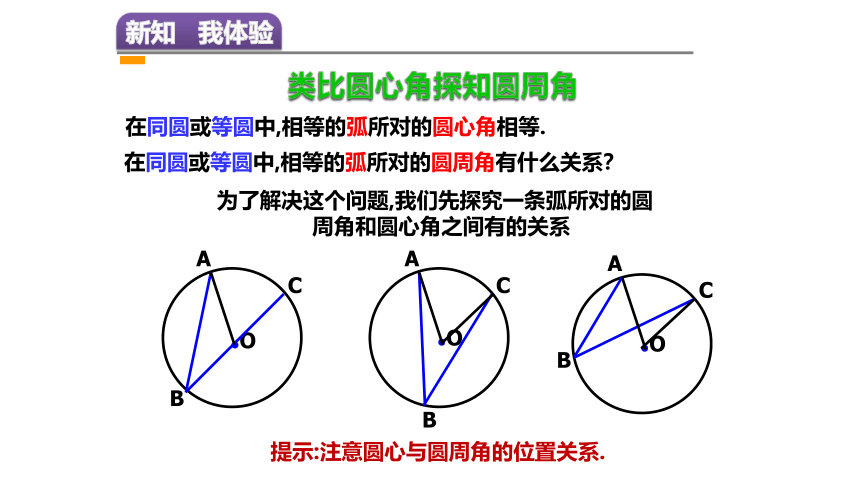
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
●O
A
B
C
A
B
C
为了解决这个问题,我们先探究一条弧所对的圆
周角和圆心角之间有的关系
类比圆心角探知圆周角
新知 我体验
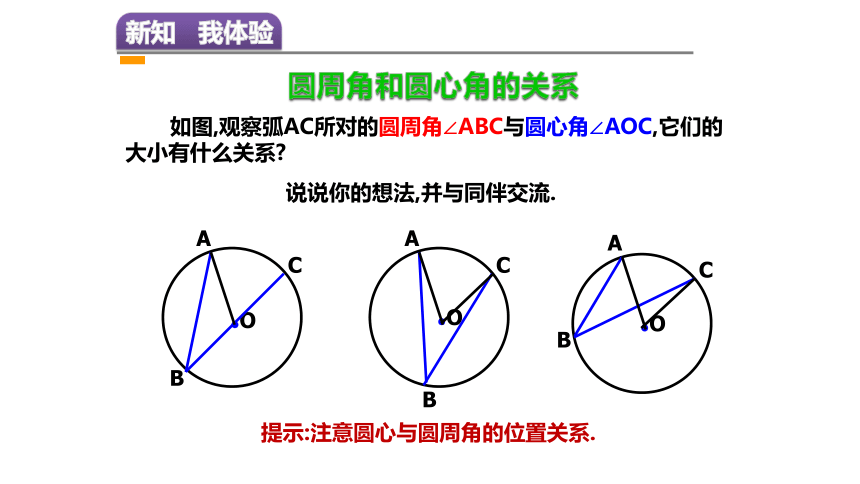
圆周角和圆心角的关系
如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
●O
●O
A
B
C
●O
A
B
C
A
B
C
说说你的想法,并与同伴交流.
提示:注意圆心与圆周角的位置关系.
新知 我体验
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心O在圆周角∠ABC的一边BC上时,圆周角∠ABC与圆心角∠AOC的大小关系.
●O
A
B
C
解:∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
即∠ABC =1/2∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
新知 我体验
圆周角和圆心角的关系
2.如果圆心不在圆周角的一边上,结果会怎样?
当圆心O在圆周角∠ABC的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
●O
A
B
C
提示:能否转化为1的情况?
过点B作直径BD.由1可得:
∴∠ABC =1/2∠AOC.
∠ABD =1/2∠AOD,
∠CBD =1/2∠COD,
D
一条弧所对的圆周角等于它所对的圆心角的一半.
新知 我体验
圆周角和圆心角的关系
3.如果圆心不在圆周角的一边上,结果会怎样?
当圆心O在圆周角∠ABC的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
●O
A
B
C
提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
∴ ∠ABC =1/2∠AOC.
∠ABD =1/2∠AOD,
∠CBD =1/2∠COD,
一条弧所对的圆周角等于它所对的圆心角的一半.
D
新知 我体验
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
圆心在角的边上
圆心在角外
圆心在角内
∠ABC =1/2 ∠AOC
D
D
拓展 我提升
1.如图:OA、OB、OC都是⊙O的半径∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
∠AOB=2∠BOC
∠ACB=2∠BAC
∠ACB=1/2∠AOB
∠BAC=1/2∠BOC
解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
拓展 我提升
2.求圆中角X的度数
B
A
O
.
70°
x
C
A
O
.
X
120°
C
D
B
3.如图,圆心角∠AOB=100°,
则∠ACB=_______
130°
O
A
B
C
反馈 我挑战
一、判断
1、顶点在圆上的角叫圆周角。
2、圆周角的度数等于所对弧的度数的一半。
×
√
.
O
36?或144°
2 、如图,已知圆心角∠AOB=100°,求圆周角∠ACB=_____、∠ADB=______。
二、计算
130?
50?
1、半径为R的圆中,有一弦分圆周成1:4两部分,则弦所对的圆周角的度数是______________
新RE-P177-1
反馈 我挑战
3、如图(1),在⊙O中,∠BAD =50°,求∠C的大小.
∠C=130?
●O
C
A
B
D
(1)
●O
B
A
C
D
E
(2)
●O
A
B
C
(3)
4 、如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系? 为什么?
5、 如图(3),AB是直径,你能确定∠C的度数吗?
∠B=∠D=∠E
∠C=90?
反馈 我挑战
6、如图,在⊙O中, CE=BD, DE=2BC, ∠ EOD=64°,求∠ A的度数。
︵
︵
A
B
C
D
E
O
反馈 我挑战
大庆第十四中学
感悟 我反思
收获总结
布 置 作 业
1、 《 课堂精练》
2、 数学A4纸
3、 想一想
感悟 我反思
努力了
就会有提高,
奋斗了
就会有收获,
拼搏了
就会有成就,
坚持了
就会有结果。
放松心态,把握自己,
相信自己,定会成功。
新知 我体验
第三章
我们的圆
圆心角顶点发生变化时,我们得到几种情况?
A
O
B
C
.
O
B
C
A
.
O
B
C
A
.
思考:三个图中的∠BAC的顶点A各在圆的什么位置?
角的两边和圆是什么关系?
5、如图,在⊙O中,BC=2DE, ∠ BOC=84°,求 ∠A的度数。
⌒
⌒
4、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35?,求∠BOC的度数。
解∵AB=AC
∴∠ABD=∠ADB=35?
∴∠BAC=∠ABD+∠ADB=70?∴∠BOC=2∠BAC=140?
解:连接CD
∵∠BOC=84?∴∠BAD= ∠BOC=42?
∵BC=2DE∴DE为42?的弧
∴∠DCE=42?× =21?
∴∠A=∠BDC-∠DCE=42?-21?=21?
⌒
⌒
⌒
圆周角和圆心角的关系第1课时
前言
二次函数结束后复习了近一周的时间,开始《圆》这一章,开始的时间为10月15号。整个这章是按北师大教材讲的,很多在人教版教材中涉及的内容都没有讲解,例如切线长\弦切角定理\相交弦定理等等。 2014届教材改版了,新调整的教材顺序很好,就用新教材的顺序了。
时间
10月15号至11月8号,但实际从8号到月末计划一直进行《二次函数》和《圆》的综合复习,这一部分的复习及计划会单独以章节形式出现。至此本部分课件结束。
内容调整1------2010版本
①《圆的对称性》中轴对称和中心对称放到了第一课时,这样在”垂径定理”处可以以一课时讲清垂径定理和后一节则讲清推论及部分应用,第三节则处理圆心角等。②《圆的对称性》这一节,由轴对称出垂径定理;由中心对称出圆心角, 弧,弦,弦心距之间的关系,正好是两路两节。③在同圆或等圆中,相等的弧所对的圆周角有什么关系?这个问题的前提是先探究一条弧所对的圆周角和圆心角之间有的关系?在《圆周角和圆心角的关系》第一课时④外心在《确定圆的条件》,而内心在《直线和圆的位置关系3课时》,注意和上学期《证明三》联系。
内容调整2------2014版本
2014届教材改版了,新调整的教材顺序很好,就用新教材的顺序了。
习题
①有时间就坚持二次函数的A4纸。课上的内容在保证速度的前提下,最好快一点,这样可以有时间去处理《倍速》。资源的习题较少,必须得配合其他练习册。
②《圆的对称性》有一道在圆中利用对称性求最短距离的题,至此正好是四道:1水站2正方形3圆4蚂蚁
③后期复习习题较多,注意保留
4.1 圆
1课时 圆的相关概念+点与圆的位置关系
4.2 圆的对称性
1课时 轴对称和中心对称+圆心角, 弧,弦,弦心距之间的关系
2课时 处理上两节课的习题
4.3 垂径定理
1课时 垂径定理9条,要求记录+推论1
2课时 推论2+垂径定理复习+赵州桥
4.4 圆周角和圆心角的关系
1课时 圆周角和圆心角关系
2课时 圆周角定理的推论1和2
4.5 确定圆的条件
1课时 确定圆的条件和外接圆等等
4.6 直线和圆的位置关系
1课时 直线和圆的位置关系及相应习题
2课时 切线的性质和判定定理
3课时 三角形外接圆和内切圆及直角三角形内切圆半径公式
4.7 切线长定理
1课时
4.8 圆内接正多边形
1课时
4.9 弧长及扇形的面积
1课时 弧长及扇形的面积
课 堂
流 程
新知 我体验
拓展 我提升
反馈 我挑战
感悟 我反思
目标 我清晰
课堂 ★ 流程
知识与技能
过程与方法
情感态度价值
1.了解圆周角的概念。2.理解圆周角定理的证明
经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化来解决一般性问题的方法,渗透分类的数学思想
通过观察、猜想、验证推理,培养学生探索问题的能力和方法
目标 我清晰
新知 我体验
圆周角
在射门游戏中,球员射中球门的难易程度与他所处的位置A对球门BC的张角(∠BAC)有关
A
B
C
.
O
B
C
A
思考:图中的∠BAC的顶点A在圆的什么位置?∠BAC的两边和圆是什么关系?
新知 我体验
.
O
B
C
A
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
圆周角定义
新知 我体验
1 、判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
2 、指出图中的圆周角
∠ACO ∠ACB ∠ BCO ∠OAB ∠BAC ∠OAC ∠ABO ∠CBO ∠ABC
新知 我体验
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.
A
B
D
E
C
新知 我体验
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
●O
A
B
C
A
B
C
为了解决这个问题,我们先探究一条弧所对的圆
周角和圆心角之间有的关系
类比圆心角探知圆周角
新知 我体验
圆周角和圆心角的关系
如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
●O
●O
A
B
C
●O
A
B
C
A
B
C
说说你的想法,并与同伴交流.
提示:注意圆心与圆周角的位置关系.
新知 我体验
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心O在圆周角∠ABC的一边BC上时,圆周角∠ABC与圆心角∠AOC的大小关系.
●O
A
B
C
解:∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
即∠ABC =1/2∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
新知 我体验
圆周角和圆心角的关系
2.如果圆心不在圆周角的一边上,结果会怎样?
当圆心O在圆周角∠ABC的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
●O
A
B
C
提示:能否转化为1的情况?
过点B作直径BD.由1可得:
∴∠ABC =1/2∠AOC.
∠ABD =1/2∠AOD,
∠CBD =1/2∠COD,
D
一条弧所对的圆周角等于它所对的圆心角的一半.
新知 我体验
圆周角和圆心角的关系
3.如果圆心不在圆周角的一边上,结果会怎样?
当圆心O在圆周角∠ABC的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
●O
A
B
C
提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
∴ ∠ABC =1/2∠AOC.
∠ABD =1/2∠AOD,
∠CBD =1/2∠COD,
一条弧所对的圆周角等于它所对的圆心角的一半.
D
新知 我体验
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
圆心在角的边上
圆心在角外
圆心在角内
∠ABC =1/2 ∠AOC
D
D
拓展 我提升
1.如图:OA、OB、OC都是⊙O的半径∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
∠AOB=2∠BOC
∠ACB=2∠BAC
∠ACB=1/2∠AOB
∠BAC=1/2∠BOC
解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
拓展 我提升
2.求圆中角X的度数
B
A
O
.
70°
x
C
A
O
.
X
120°
C
D
B
3.如图,圆心角∠AOB=100°,
则∠ACB=_______
130°
O
A
B
C
反馈 我挑战
一、判断
1、顶点在圆上的角叫圆周角。
2、圆周角的度数等于所对弧的度数的一半。
×
√
.
O
36?或144°
2 、如图,已知圆心角∠AOB=100°,求圆周角∠ACB=_____、∠ADB=______。
二、计算
130?
50?
1、半径为R的圆中,有一弦分圆周成1:4两部分,则弦所对的圆周角的度数是______________
新RE-P177-1
反馈 我挑战
3、如图(1),在⊙O中,∠BAD =50°,求∠C的大小.
∠C=130?
●O
C
A
B
D
(1)
●O
B
A
C
D
E
(2)
●O
A
B
C
(3)
4 、如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系? 为什么?
5、 如图(3),AB是直径,你能确定∠C的度数吗?
∠B=∠D=∠E
∠C=90?
反馈 我挑战
6、如图,在⊙O中, CE=BD, DE=2BC, ∠ EOD=64°,求∠ A的度数。
︵
︵
A
B
C
D
E
O
反馈 我挑战
大庆第十四中学
感悟 我反思
收获总结
布 置 作 业
1、 《 课堂精练》
2、 数学A4纸
3、 想一想
感悟 我反思
努力了
就会有提高,
奋斗了
就会有收获,
拼搏了
就会有成就,
坚持了
就会有结果。
放松心态,把握自己,
相信自己,定会成功。
新知 我体验
第三章
我们的圆
圆心角顶点发生变化时,我们得到几种情况?
A
O
B
C
.
O
B
C
A
.
O
B
C
A
.
思考:三个图中的∠BAC的顶点A各在圆的什么位置?
角的两边和圆是什么关系?
5、如图,在⊙O中,BC=2DE, ∠ BOC=84°,求 ∠A的度数。
⌒
⌒
4、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35?,求∠BOC的度数。
解∵AB=AC
∴∠ABD=∠ADB=35?
∴∠BAC=∠ABD+∠ADB=70?∴∠BOC=2∠BAC=140?
解:连接CD
∵∠BOC=84?∴∠BAD= ∠BOC=42?
∵BC=2DE∴DE为42?的弧
∴∠DCE=42?× =21?
∴∠A=∠BDC-∠DCE=42?-21?=21?
⌒
⌒
⌒
