北师大版九年级数学下册第1章第2节30° ,45°, 60°角的三角函数值 (1)(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第1章第2节30° ,45°, 60°角的三角函数值 (1)(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 423.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 23:06:28 | ||
图片预览

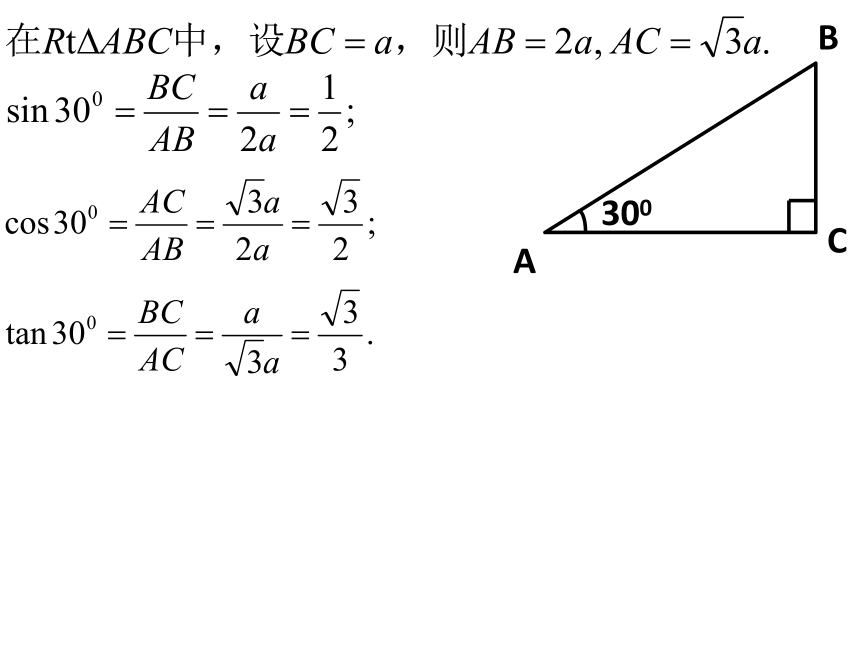



文档简介
第一章 直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
b
A
B
C
a
┌
c
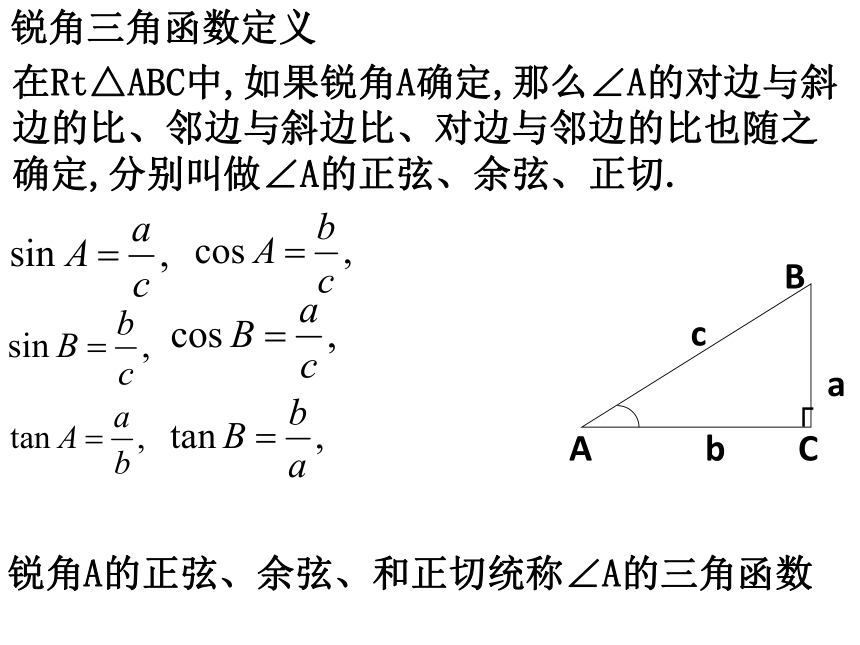
锐角A的正弦、余弦、和正切统称∠A的三角函数
锐角三角函数定义
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边比、对边与邻边的比也随之确定,分别叫做∠A的正弦、余弦、正切.
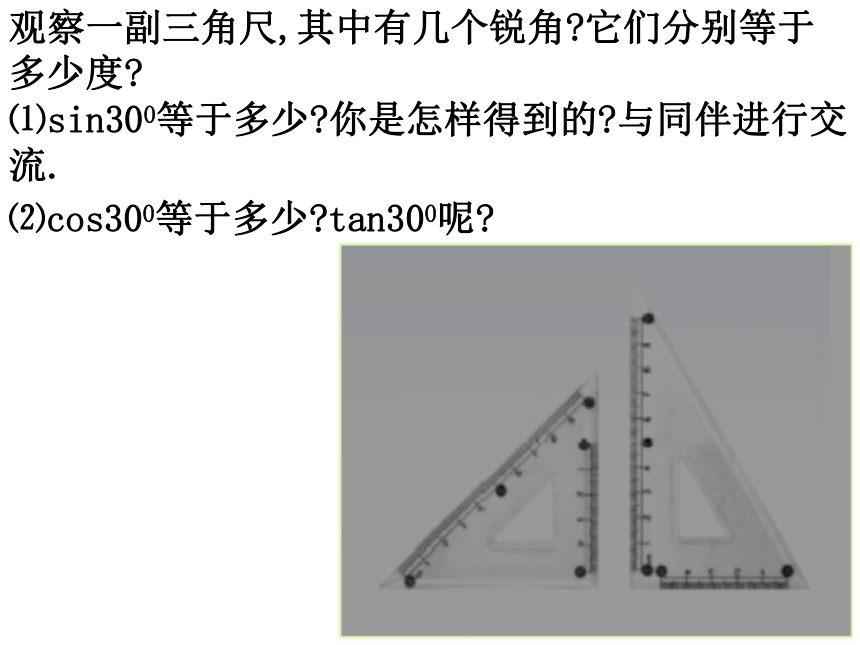
观察一副三角尺,其中有几个锐角?它们分别等于多少度?
⑴sin300等于多少?你是怎样得到的?与同伴进行交流.
⑵cos300等于多少?tan300呢?
A
B
C
300
⑴600角的三角函数值分别是多少?你是怎样得到的?
做一做
求600角的三角函数值可以利用求300角的三角函数值的三角形。此时300角的对边和邻边分别是600角的邻边和对边。
A
B
C
300
600
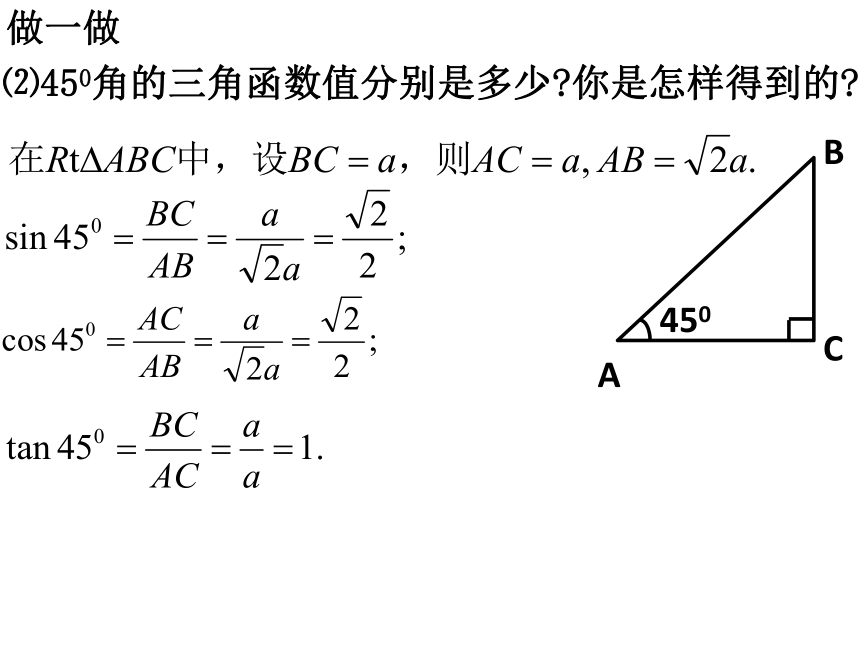
⑵450角的三角函数值分别是多少?你是怎样得到的?
做一做
A
B
C
450
sinα
cosα
tanα
30°
45°
60°
1
做一做
⑶完成下表:
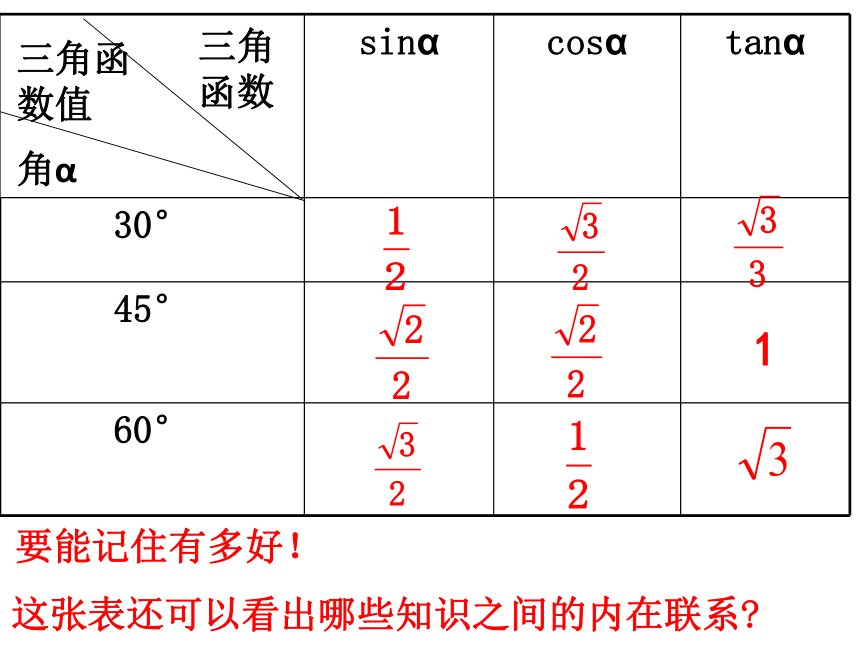
特殊角的三角函数值表
角α
三角函数值
三角函数
sinα
cosα
tanα
30°
45°
60°
1
角α
三角函数值
三角函数
这张表还可以看出哪些知识之间的内在联系?
要能记住有多好!
例1 计算:
(1)sin300+cos450;(2) sin2600+cos2600-tan450.
提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
解: (1)sin300+cos450
(2) sin2600+cos2600-tan450
例2 一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
将实际问题数学化
解:如图,根据题意可知,
∠AOD= ×600=300,OD=2.5m,
∴OC=ODcos300
=2.5×
≈2.165
∴AC=2.5-2.165 ≈0.34 (m)
所以,最高位置与最低位置的高度差约为0.34m.
(1)sin600-tan450;
(2)cos600+tan600;
练习
计算:
计算;
(1)tan450-sin300;
(2)cos600+sin450-tan300;
某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少?
14m.
如图,河岸AD,BC互相平行,桥AB垂直于两岸.桥长12m,在C处看桥两端A,B,夹角∠BCA=600.求B,C间的距离(结果精确到1m).
在Rt△ABC中,
∴BC≈7m.
如图,SO是等腰三角形SAB的高,已知∠ASB=1200,AB=54,求SO的长。
如图,身高1.75m的小丽用一个两锐角分别是300和600 的三角尺测量一棵树的高度(∠A=300).已知她与树之间的距离为5m,那么这棵树大约有多高?(结果精确到0.1m)
树高约4.6m.
如图,一段长1500m的水渠,它的横截面为梯形ABCD,其中AB∥CD,BC=AD,渠深AE=0.8m,底AB=1.2m,坡角为450,那么该段水渠最多能蓄水多少立方米?
2400m3.
某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为450,BC部分的坡角为300,AD=1.5m.如果每个台阶的高不超过20cm,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm时,按一个台阶计算)
已知∠A为锐角,且cosA= ,你能求出∠A的度数吗。
已知a为锐角,tan(90°-a)= ,求a.
在Rt△ABC中, ∠C=90°,若cosB= ,求sinA
在△ABC中, 若| sinA- |+(1- tanB)=0,求∠C
D
A
B
C
某片绿化地的形状如图所示,其中∠A=600,AB⊥BC,AD⊥CD,AB=200m,CD=100m.求AD,BC的长。
某市在“旧城改造”中计划内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米a元,则购买这种草皮至少要多少元.
小结:
学完本课后你有哪些收获?
作业:
习题1.3 1、2、3、4、5、6题。
1.2 30°,45°,60°角的三角函数值
b
A
B
C
a
┌
c
锐角A的正弦、余弦、和正切统称∠A的三角函数
锐角三角函数定义
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边比、对边与邻边的比也随之确定,分别叫做∠A的正弦、余弦、正切.
观察一副三角尺,其中有几个锐角?它们分别等于多少度?
⑴sin300等于多少?你是怎样得到的?与同伴进行交流.
⑵cos300等于多少?tan300呢?
A
B
C
300
⑴600角的三角函数值分别是多少?你是怎样得到的?
做一做
求600角的三角函数值可以利用求300角的三角函数值的三角形。此时300角的对边和邻边分别是600角的邻边和对边。
A
B
C
300
600
⑵450角的三角函数值分别是多少?你是怎样得到的?
做一做
A
B
C
450
sinα
cosα
tanα
30°
45°
60°
1
做一做
⑶完成下表:
特殊角的三角函数值表
角α
三角函数值
三角函数
sinα
cosα
tanα
30°
45°
60°
1
角α
三角函数值
三角函数
这张表还可以看出哪些知识之间的内在联系?
要能记住有多好!
例1 计算:
(1)sin300+cos450;(2) sin2600+cos2600-tan450.
提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
解: (1)sin300+cos450
(2) sin2600+cos2600-tan450
例2 一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
将实际问题数学化
解:如图,根据题意可知,
∠AOD= ×600=300,OD=2.5m,
∴OC=ODcos300
=2.5×
≈2.165
∴AC=2.5-2.165 ≈0.34 (m)
所以,最高位置与最低位置的高度差约为0.34m.
(1)sin600-tan450;
(2)cos600+tan600;
练习
计算:
计算;
(1)tan450-sin300;
(2)cos600+sin450-tan300;
某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少?
14m.
如图,河岸AD,BC互相平行,桥AB垂直于两岸.桥长12m,在C处看桥两端A,B,夹角∠BCA=600.求B,C间的距离(结果精确到1m).
在Rt△ABC中,
∴BC≈7m.
如图,SO是等腰三角形SAB的高,已知∠ASB=1200,AB=54,求SO的长。
如图,身高1.75m的小丽用一个两锐角分别是300和600 的三角尺测量一棵树的高度(∠A=300).已知她与树之间的距离为5m,那么这棵树大约有多高?(结果精确到0.1m)
树高约4.6m.
如图,一段长1500m的水渠,它的横截面为梯形ABCD,其中AB∥CD,BC=AD,渠深AE=0.8m,底AB=1.2m,坡角为450,那么该段水渠最多能蓄水多少立方米?
2400m3.
某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为450,BC部分的坡角为300,AD=1.5m.如果每个台阶的高不超过20cm,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm时,按一个台阶计算)
已知∠A为锐角,且cosA= ,你能求出∠A的度数吗。
已知a为锐角,tan(90°-a)= ,求a.
在Rt△ABC中, ∠C=90°,若cosB= ,求sinA
在△ABC中, 若| sinA- |+(1- tanB)=0,求∠C
D
A
B
C
某片绿化地的形状如图所示,其中∠A=600,AB⊥BC,AD⊥CD,AB=200m,CD=100m.求AD,BC的长。
某市在“旧城改造”中计划内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米a元,则购买这种草皮至少要多少元.
小结:
学完本课后你有哪些收获?
作业:
习题1.3 1、2、3、4、5、6题。
