北师大版九年级数学下册第二章教学课件:2.4.1 应用二次函数 求几何图形最值(共21张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第二章教学课件:2.4.1 应用二次函数 求几何图形最值(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 22:50:06 | ||
图片预览







文档简介
第二章
二次函数
2.4.1 应用二次函数求几何图形最值
教学目标
1.掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.(重点)
2.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.(难点)
新课导入
情境引入
二次函数的最值求法:
①当a>0时,y有最小值=
②当a<0时,y有最大值=
二次函数
顶点坐标为
新课导入
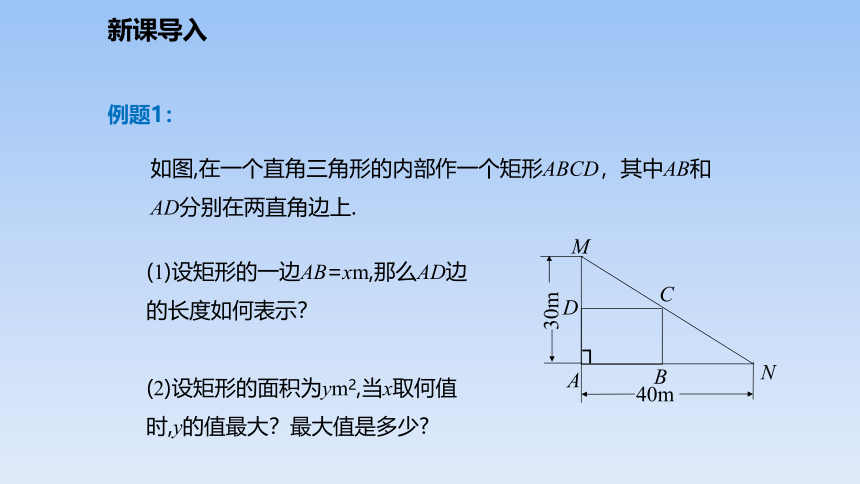
(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
M
N
40m
30m
A
B
C
D
┐
例题1:
新课导入
解析:
新知探究
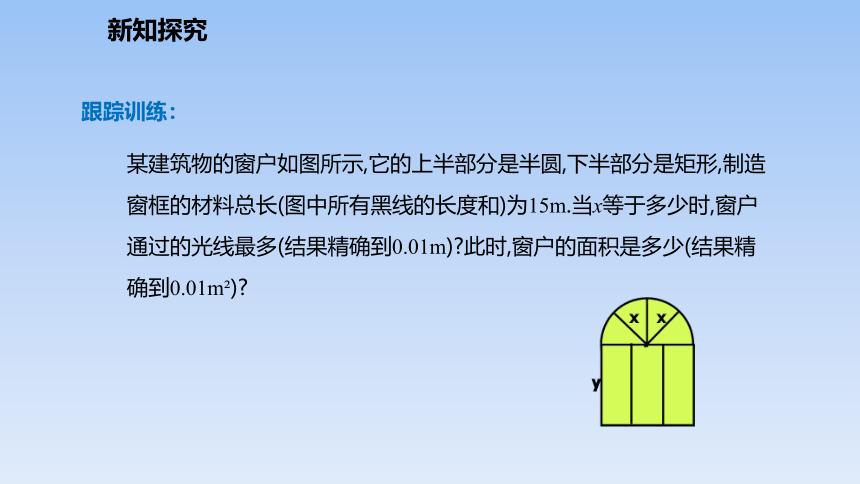
某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少(结果精确到0.01m?)?
跟踪训练:
新知探究
解:
因此,当x≈1.07m时,窗户通过的光线最多,此时窗户的面积约是 4.02m2.
新知探究
例题2 :
在美化城市的建设中,某街道想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.
(1)若花园的面积为195m2,求x的值.
(2)若在P处有一棵树与墙CD,AD的距离分别是6m和8m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S(m2)的最大值.
新知探究
(1)根据题意,BC=xm,则AB=(28-x)m,故x(28-x)=195,
解得x=13或x=15.
解 :
(2)∵P与墙CD,AD的距离分别是6m和8m,
∴x≥6且28-x≥8,解得6≤x≤20,
由题意可得S=x(28-x)=-x?+28x
=-(x-14)2+196,
∴当x=14时,S取得最大值,最大值为196.
答:花园面积S的最大值为196m2.
课堂小结
“最大面积” 问题解决的基本思路:
1.阅读题目,理解问题.
2.分析问题中的变量和常量以及它们之间的关系.
3.用数量关系式表示出它们之间的关系.
4.根据二次函数的最值问题求出最大值、最小值.
5.检验结果的合理性.
规律方法:
课堂小结
先将实际问题转化为数学问题,再将所求的问题用二次函数关系式表达出来,然后利用顶点坐标公式或者配方法求出最值,有时必须考虑其自变量的取值范围,根据图象求出最值.
课堂小测
1.用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2x m.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
课堂小测
解:
根据题意,可得
m,
m
m
m
m
课堂小测
2.学校计划用地面砖铺设教学楼前的矩形广场的地面ABCD,已知矩形广场地面的长为100米,宽为80米,图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都是小正方形的边长,阴影部分铺设绿色地面砖,其余部分铺设白色地面砖.
(1)要使铺设白色地面砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为多少米?
(2)如图铺设白色地面砖的费用为每平方米30元,铺设绿
色地面砖的费用为每平方米20元.当广场四角小正方形的边
长为多少米时,铺设广场地面的总费用最少?最少费用是多
少?
课堂小测
(1)、设矩形广场四角的小正方形的边长为x米.
根据题意,得4x2+(100-2x)(80-2x)=5200,
整理得x2-45x+350=0,
解得x1=35,x2=10,经检验x1=35,x2=10均适合题意,
所以要使铺设白色地面砖的面积为5200平方米,
则矩形广场四角的小正方形的边长为35米或者10米.
解 :
课堂小测
(2)设铺设矩形广场地面的总费用为y元,
广场四角的小正方形的边长为x米,则
y=30[4x2+(100-2x)(80-2x)]+20[2x(100-2x)+2x(80-2x)]
即y=80x2-3600x+240000,配方得
y=80(x-22.5)2+199500,
当x=22.5时,y的值最小,最小值为199500,
所以当矩形广场四角的小正方形的边长为22.5米时,
铺设矩形广场地面的总费用最少,最少费用为199500元.
课堂小测
课堂小测
(1)在矩形ABCD中,∠B=∠C=90°,
∴在Rt△BFE中, ∠1+∠BFE=90°,
又∵EF⊥DE, ∴∠1+∠2=90°,
∴∠2=∠BFE,
∴Rt△BFE∽Rt△CED,
解:
课堂小测
∵△DEF中∠FED是直角,
∴要使△DEF是等腰三角形,则只能是EF=ED,此时,Rt△BFE≌Rt△CED,
(2)当m=8时,
∴当x=4时,y的值最大,最大值是2.
即△DEF为等腰三角形,m的值应为6或2.
当EC=6时,
m=CD=BE=2,
m=CD=BE=6;
∴当EC=2时,
化成顶点式:
,得
x
得关于x的方程:
(3)由
,及
x
课堂小测
4.如图,东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.
(1)求y与x的函数关系式,并求出自变量x的取值范围.
(2)生物园的面积能否达到210平方米?说明理由.
课堂小测
(1)依题意得y=(40-2x)x.
∴y=-2x2+40x.
x的取值范围是0< x <20.
(2)当y=210时,由(1)可得-2x2+40x=210.
即x2-20x+105=0.
∵ a=1,b=-20,c=105,
∴此方程无实数根,即生物园的面积不能达到210平方米.
解:
∴
,
二次函数
2.4.1 应用二次函数求几何图形最值
教学目标
1.掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.(重点)
2.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.(难点)
新课导入
情境引入
二次函数的最值求法:
①当a>0时,y有最小值=
②当a<0时,y有最大值=
二次函数
顶点坐标为
新课导入
(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
M
N
40m
30m
A
B
C
D
┐
例题1:
新课导入
解析:
新知探究
某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少(结果精确到0.01m?)?
跟踪训练:
新知探究
解:
因此,当x≈1.07m时,窗户通过的光线最多,此时窗户的面积约是 4.02m2.
新知探究
例题2 :
在美化城市的建设中,某街道想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.
(1)若花园的面积为195m2,求x的值.
(2)若在P处有一棵树与墙CD,AD的距离分别是6m和8m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S(m2)的最大值.
新知探究
(1)根据题意,BC=xm,则AB=(28-x)m,故x(28-x)=195,
解得x=13或x=15.
解 :
(2)∵P与墙CD,AD的距离分别是6m和8m,
∴x≥6且28-x≥8,解得6≤x≤20,
由题意可得S=x(28-x)=-x?+28x
=-(x-14)2+196,
∴当x=14时,S取得最大值,最大值为196.
答:花园面积S的最大值为196m2.
课堂小结
“最大面积” 问题解决的基本思路:
1.阅读题目,理解问题.
2.分析问题中的变量和常量以及它们之间的关系.
3.用数量关系式表示出它们之间的关系.
4.根据二次函数的最值问题求出最大值、最小值.
5.检验结果的合理性.
规律方法:
课堂小结
先将实际问题转化为数学问题,再将所求的问题用二次函数关系式表达出来,然后利用顶点坐标公式或者配方法求出最值,有时必须考虑其自变量的取值范围,根据图象求出最值.
课堂小测
1.用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2x m.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
课堂小测
解:
根据题意,可得
m,
m
m
m
m
课堂小测
2.学校计划用地面砖铺设教学楼前的矩形广场的地面ABCD,已知矩形广场地面的长为100米,宽为80米,图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都是小正方形的边长,阴影部分铺设绿色地面砖,其余部分铺设白色地面砖.
(1)要使铺设白色地面砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为多少米?
(2)如图铺设白色地面砖的费用为每平方米30元,铺设绿
色地面砖的费用为每平方米20元.当广场四角小正方形的边
长为多少米时,铺设广场地面的总费用最少?最少费用是多
少?
课堂小测
(1)、设矩形广场四角的小正方形的边长为x米.
根据题意,得4x2+(100-2x)(80-2x)=5200,
整理得x2-45x+350=0,
解得x1=35,x2=10,经检验x1=35,x2=10均适合题意,
所以要使铺设白色地面砖的面积为5200平方米,
则矩形广场四角的小正方形的边长为35米或者10米.
解 :
课堂小测
(2)设铺设矩形广场地面的总费用为y元,
广场四角的小正方形的边长为x米,则
y=30[4x2+(100-2x)(80-2x)]+20[2x(100-2x)+2x(80-2x)]
即y=80x2-3600x+240000,配方得
y=80(x-22.5)2+199500,
当x=22.5时,y的值最小,最小值为199500,
所以当矩形广场四角的小正方形的边长为22.5米时,
铺设矩形广场地面的总费用最少,最少费用为199500元.
课堂小测
课堂小测
(1)在矩形ABCD中,∠B=∠C=90°,
∴在Rt△BFE中, ∠1+∠BFE=90°,
又∵EF⊥DE, ∴∠1+∠2=90°,
∴∠2=∠BFE,
∴Rt△BFE∽Rt△CED,
解:
课堂小测
∵△DEF中∠FED是直角,
∴要使△DEF是等腰三角形,则只能是EF=ED,此时,Rt△BFE≌Rt△CED,
(2)当m=8时,
∴当x=4时,y的值最大,最大值是2.
即△DEF为等腰三角形,m的值应为6或2.
当EC=6时,
m=CD=BE=2,
m=CD=BE=6;
∴当EC=2时,
化成顶点式:
,得
x
得关于x的方程:
(3)由
,及
x
课堂小测
4.如图,东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.
(1)求y与x的函数关系式,并求出自变量x的取值范围.
(2)生物园的面积能否达到210平方米?说明理由.
课堂小测
(1)依题意得y=(40-2x)x.
∴y=-2x2+40x.
x的取值范围是0< x <20.
(2)当y=210时,由(1)可得-2x2+40x=210.
即x2-20x+105=0.
∵ a=1,b=-20,c=105,
∴此方程无实数根,即生物园的面积不能达到210平方米.
解:
∴
,
