北师大版七年级上册第五章一元一次方程章末复习课件(31ppt)
文档属性
| 名称 | 北师大版七年级上册第五章一元一次方程章末复习课件(31ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 343.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览











文档简介
第五章一元一次方程章末复习
七年级上册
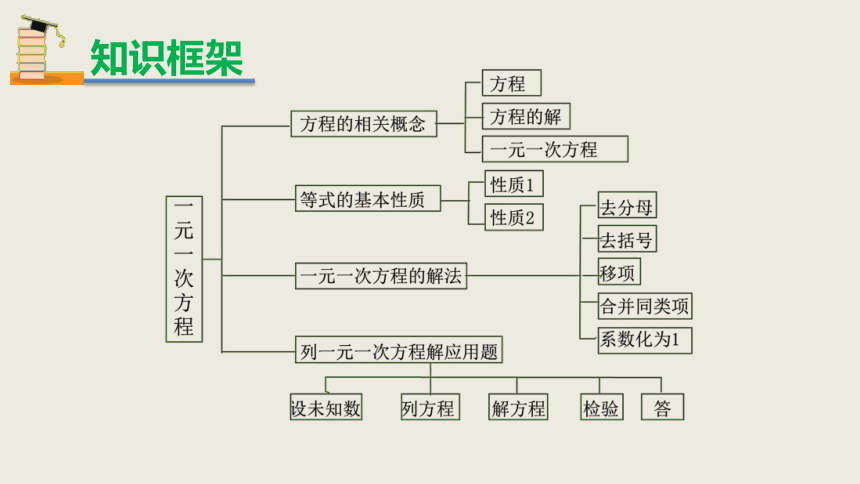
知识框架
(一)认识和求解一元一次方程
1. 一元一次方程的概念:只含有一个未知数,并且未知数的次数都是1的方程叫做一元一次方程。?
一元一次方程的标准形式:ax+b=0(其中x是未知数,a,b是已知数,且a≠0).?
一元一次方程的基本要素:①是等式;②只含有一个未知数(化简后),③未知数的次数是1(化简后).
2.方程的解:使方程左右两边的值相等的未知数的值叫做方程的解.
判断一个数是否是某方程的解:将其代入方程两边,看两边是否相等.
知识回顾
(一)认识和求解一元一次方程
3.等式的基本性质:
(1)等式的两边同时加上或减去同一个代数式,所得结果仍然是等式;
(2)等式的两边同时乘上同一个数或除以同一个不为0的整式,所得结果仍然是等式.
4.解一元一次方程的基本思路:?
通过对方程变形,把含有未知数的项归到方程的一边,把常数项归到方程的另一边,最终把方程“转化”成x=a的形式.
知识回顾
(一)认识和求解一元一次方程
5.解一元一次方程的一般步骤是:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}变形名称
具体做法
变形依据
去分母
去括号
移项
合并同类项
系数化成1
知识回顾
在方程两边都乘以各分母的最小公倍数
等式基本性质2
先去小括号,再去中括号,最后去大括号
去括号法则、分配律
把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(记住移项要变号)
等式基本性质1?
把方程化成ax=b(a≠0)的形式
合并同类项法则
在方程两边都除以未知数的系数a,得x=b/a
等式基本性质2
1. 下列各式中,是一元一次方程的是( )
A.x+y=x-2 B.x+y=5 C.4x=0 D.6x+5
2. 下列方程的解不是x= 的是( )
A.2x=1 B.-2x+2=3 C.x=1-x D. (x-1)=-
C
B
考点对接
3. 若代数式2x+1和x+5的值相等,x的值为( )
A.2 B.3 C.4 D.5
4. 如果2 005-200.5=x-20.05,那么x等于( )
A.1 814.15 B.1 824.55 C.1 774.45 D.1 784.45
5. 如果关于m的方程2m+b=m-1的解是-4,那么b的值为( )
A.3 B.5 C.-5 D.-13
C
B
A
考点对接
6. 已知方程(m+1)x |m| +3=0是关于x的一元一次方程,则m的值是( )
A.±1 B.1 C.-1 D.0或1
分析:方程(m+1)x |m| +3=0是关于x的一元一次方程,则m+1≠0,|m|=1,所以m=1.答案:B
7. 方程 ,去分母,得( )
A.2x-1-x+1=6 B.3(2x-1)-2(x+1)=6
C.2(2x-1)-3(x+1)=6 D.3x-3-2x-2=1
分析:根据等式的基本性质:方程的两边同乘以6,方程的解不变.答案:B
B
B
考点对接
8. 如果5a 3 b 5(m-1)与a 3 b 6m-7 是同类项,那么m的值为( )
A.-4 B.2 C.-2 D.4
分析:根据同类项的定义,转化为方程.5(m-1)=6m-7,解得m=2.故选B. 答案:B
9.如果式子x+2与-2x+4的值是互为相反数,则x的值?
解:根据互为相反的两数之和等于0 可得
x+2+(-2x+4)=0
x+2-2x+4=0
-x+6=0
- x =-6
x =6 所以x的值为6
B
考点对接
10. 解方程:3(x+1)-(5+x)=18-2(x-1).
解:去括号,得3x+3-5-x=18-2x+2;
移项,得 3x-x+2x=18+2-3+5;
合并同类项,得 4x=22.
系数化为1,得 x= .
考点对接
12. 解方程:5x-|x|=8.
解:当x≥0时,原式化为
5x-x=8
4x=8
x=2
当x<0时,原式化为
5x-(-x)=8
6x=8
x= (不满足x<0的条件,所以不符合要求,应舍去)
方程的解为x=2
考点对接
13. 已知x 2m-3 +6=m是关于x的一元一次方程,试求代数式(m-3) 2 006 的值.
解:由已知x 2m-3 +6=m是关于x的一元一次方程,
得2m-3=1;
解之,得m=2;
从而(m-3) 2 006
=(2-3) 2 006
=(-1) 2 006 =1.
考点对接
(二)列一元一次方程解应用题
1.一般步骤
(1)审题,分析题中已知什么,未知什么,明确各量之间的关系,寻找等量关系;
(2)设未知数,一般求什么就设什么为x,但有时也可以间接设未知数;
(3)列方程,把相等关系左右两边的量用含有未知数的代数式表示出来,列出方程;
(4)解方程;
(5)检验,看该解是否是方程的解、是否符合题意.
(6)写出答案.
知识回顾
1. 要锻造一个直径为 8 cm 、高为 4 cm 的圆柱形毛坯,至少应截取直径为 4 cm 的圆钢的长度为( ).
A.6cm B.10cm C.16cm D. 20cm
分析:设圆钢为x cm,则π(2)2 x=π(4)2 ×4,
解得x=16. 答案:C
C
考点对接
2. 某商店在某一时间以每件50元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,在这次买卖中,该家商店( )
A.亏损6.7元 B.盈利6.7元 C.不亏不盈 D.以上都不正确
分析:设盈利25%的那件衣服的进价是x元,
根据进价与利润的和等于售价列得方程:x+0.25x=50,
解得:x=40,
类似地,设另一件亏损衣服的进价为y元,它的商品利润是-25%y元,
列方程y+(-25%y)=50,
解得:y=66.7.
那么这两件衣服的进价是x+y=106.7元,而两件衣服的售价为100元.
∴100-106.7=-6.7元,
所以,该家商店亏损6.7元.故选: A.
A
考点对接
3. 某人以八折的优惠价购买一套服装节省15元,那么这个人购买这套服装用去( )
A.35元 B.60元 C.75元 D.150元
4. 某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分加倍收费.某职工某月交水费16m元,则该职工这个月实际用水为( )
A.13立方米 B.14立方米 C.18立方米 D.26立方米
B
A
考点对接
5. 甲、乙两人从同一地点出发前往某地,若乙先走1小时,甲从后面追赶,当甲追上乙时,不成立的是( )
A.乙比甲先走1小时
B.甲、乙两人行程之和等于出发地和相遇地两点距离的2倍
C.乙走的路程比甲多 D.甲、乙两人所走的路程相等
6. 教室里有40套课桌椅,共计2 800元,每把椅子20元,问每张桌子多少元?设每张桌子x元,可列方程为( )
A.40x+20=2 800 B.40x+40×20=2 800
C.40x+20(40-x)=2 800 D.40(x-20)=2 800
C
B
考点对接
7. 小亮家今年承包的鱼塘到期了,共起出鲫鱼和鳊鱼500千克,共卖了2800元,已知鲫鱼和鳊鱼每千克分别为6元和5元,则鲫鱼和鳊鱼各千克.
解:设鲫鱼x千克,则鳊(500-x)千克,
由题意得 6x+5(500-x)=2800
解得x=300
则鳊(500-x)=500-300=200
答:鲫鱼300千克,鳊鱼200千克.
考点对接
8. A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x+80=240
解得 x=2
答:设B车行了2小时后与A车相距80千米。
考点对接
9.环湖一周800米,甲练习骑自行车平均每分钟行300米,乙练习跑步平均每分钟跑200米,两人同时同地出发.
(1)若两人背向而行,则他们经过多少时间首次相遇?
(2)若两人同向而行,则他们经过多少时间首次相遇?
解:(1)设相遇的时间为x,
根据题意就有500x+200x=800,
解得x≈1.143,故大约经过1.143分钟他们首次相遇.
(2)设相遇的时间为y,
根据题意就有500y-200y=800,
解得y≈2.67,故大约经过2.67分钟首次相遇.
考点对接
10. 某市居民生活用电基本价格为每度0.40元,若每月用电量超过a度,超出部分按基本电价的70%收费.
(1)某户五月份用电84度,共交电费30.72元,求a.
(2)若该户六月份的电费平均为每度0.36元,求六月份共用电多少度?应交电费多少元?
解:(1)由题意,有这样的相等关系:
a度电的电费+超出a度的那部分电费=五月份总电费,
由此得方程0.40a+(84-a)×0.40×70%=30.72,
解得a=60.
(2)设该户六月份共用电x度,由题意,有相等关系:
60度电的电费+超出60度的那部分电费=六月份总电费,
由此得方程0.40×60+(x-60)×0.40×70%=0.36x,
解得x=90,则0.36x=32.40.
答:该户六月份共用电90度,应交电费32.40元.
考点对接
11.北魏著名数学家张丘建撰写的《张丘建算经》:今有甲、乙怀银,不知其数,乙得甲十银,适等;甲得乙十银,多乙余钱5倍,问甲、乙怀银各几何?
分析:甲乙两人各有钱若干,若甲给乙十个钱,则两人的钱数刚好相等,则甲比乙多的钱,若乙给甲10个钱,甲是乙余下来的钱数多5倍;问:两人原来各有多少钱?
解:设甲怀银x枚,则乙怀银(x-20)枚,由题意得
x+10=6(x-20-10),
解得x=38,x-20=18 ,
答:甲怀银38枚,乙怀银18枚.
考点对接
1.下列方程是一元一次方程的是( )
A.x2=25 B.x-5=6 C. 3x-y=6 D. =2
2.若(m-1)x|m|+5=0是一元一次方程,则m的值为( )
A.1 B.-1 C.±1 D.不能确定
3.已知关于x的方程5x+3k=24与方程5x+3=0的解相同,则k的值是( )
A.7 B.-8 C.-10 D.9
B
B
D
随堂检测
4.解下列方程:
(1)2(x+3)=5(x-3); (2)
解:(1)2x+6=5x-15
-3x=-21
x=7
随堂检测
(2)10x-5=12-9x-15x
34x=17
x= .
5.已知关于x的方程 的解比方程5(x-1)-1=4(x-1)+1的解大2. (1)求第二个方程的解; (2)求m的值.
解:(1)5(x-1)-1=4(x-1)+1
5x-5-1=4x-4+1
5x-4x=-4+1+1+5
x=3.
(2)由题意得:方程 的解为x=3+2=5,
把x=5代入方程 ,得
,解得m=22.
随堂检测
6.甲、乙两人从A地出发前往B地,甲出发2小时后,乙开始出发,已知甲的速度是15 km/h,乙的速度是60 km/h,A,B两地相距100 km,乙追上甲的地方离B地多远?
解:设乙出发x h后追上甲,则此时甲出发了(x+2)h.
根据题意,得60x=15(x+2),
解得x=23 ,
∴100-60x=100-60×23=60.
则乙追上甲的地方离B地60 km.
?
随堂检测
7.整理一批图书,由一个人做要40小时完成.现计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
解:设应先安排x人工作.
根据题意,得 ,
化简可得 x+2(x+2)=10,
解得x=2,
则应先安排2人工作.
随堂检测
8.入冬以来,某家电销售部以150元/台的价格购进一款烤火器,很快售完,又用相同的货款再次购进这款烤火器.因单价提高了30元,进货量比第一次少了10台.
(1)家电销售部两次各购进烤火器多少台?
(2)若以250元/台的售价卖完这两批烤火器,家电销售部共获利多少元?
解:(1)设第一次购进烤火器x台,则第二次购进烤火器(x-10)台.
根据题意得150x=180(x-10),
解得x=60,x-10=50.
则家电销售部第一次购进烤火器60台,第二次购进50台.
(2)(250-150)×60+(250-180)×50=9 500(元).
故家电销售部共获利9 500元.
随堂检测
9.甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物x元(x>300).
(1)请用含x代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
解:(1)设顾客在甲超市购物所付的费用为y甲,顾客在乙超市购物所付的费用为y乙,
根据题意得y甲=300+0.8(x-300)=0.8x+60;y乙=200+0.85(x-200)=0.85x+30.
(2)他应该去乙超市,理由如下:当x=500时,y甲=0.8x+60=460,y乙=0.85x+30=455,
∵460>455,∴他去乙超市划算.
(3)令y甲=y乙,即0.8x+60=0.85x+30,解得x=600.
则李明购买600元的商品时,到两家超市购物所付的费用一样.
随堂检测
10.请根据图中提供的信息,回答下列问题:
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算?并说明理由.(必须在同一家购买)
解:(1)设一个水瓶x元,表示出一个水杯为(48-x)元.根据题意得
3x+4(48-x)=152,解得x=40,
则一个水瓶是40元,一个水杯是8元.
(2)甲商场所需费用为(40×5+8×20)×80%=288(元).
乙商场所需费用为5×40+(20-5×2)×8=280(元).
∵288>280,∴选择乙商场购买更合算.
随堂检测
本章知识重点
1.一元一次方程
2.解一元一次方程
3.一元一次方程的应用
温馨提示
1.化简后分母中含有未知数的方程不是一元一次方程
2.去分母时不要漏乘不含分母的项
课堂小结
七年级上册
知识框架
(一)认识和求解一元一次方程
1. 一元一次方程的概念:只含有一个未知数,并且未知数的次数都是1的方程叫做一元一次方程。?
一元一次方程的标准形式:ax+b=0(其中x是未知数,a,b是已知数,且a≠0).?
一元一次方程的基本要素:①是等式;②只含有一个未知数(化简后),③未知数的次数是1(化简后).
2.方程的解:使方程左右两边的值相等的未知数的值叫做方程的解.
判断一个数是否是某方程的解:将其代入方程两边,看两边是否相等.
知识回顾
(一)认识和求解一元一次方程
3.等式的基本性质:
(1)等式的两边同时加上或减去同一个代数式,所得结果仍然是等式;
(2)等式的两边同时乘上同一个数或除以同一个不为0的整式,所得结果仍然是等式.
4.解一元一次方程的基本思路:?
通过对方程变形,把含有未知数的项归到方程的一边,把常数项归到方程的另一边,最终把方程“转化”成x=a的形式.
知识回顾
(一)认识和求解一元一次方程
5.解一元一次方程的一般步骤是:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}变形名称
具体做法
变形依据
去分母
去括号
移项
合并同类项
系数化成1
知识回顾
在方程两边都乘以各分母的最小公倍数
等式基本性质2
先去小括号,再去中括号,最后去大括号
去括号法则、分配律
把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(记住移项要变号)
等式基本性质1?
把方程化成ax=b(a≠0)的形式
合并同类项法则
在方程两边都除以未知数的系数a,得x=b/a
等式基本性质2
1. 下列各式中,是一元一次方程的是( )
A.x+y=x-2 B.x+y=5 C.4x=0 D.6x+5
2. 下列方程的解不是x= 的是( )
A.2x=1 B.-2x+2=3 C.x=1-x D. (x-1)=-
C
B
考点对接
3. 若代数式2x+1和x+5的值相等,x的值为( )
A.2 B.3 C.4 D.5
4. 如果2 005-200.5=x-20.05,那么x等于( )
A.1 814.15 B.1 824.55 C.1 774.45 D.1 784.45
5. 如果关于m的方程2m+b=m-1的解是-4,那么b的值为( )
A.3 B.5 C.-5 D.-13
C
B
A
考点对接
6. 已知方程(m+1)x |m| +3=0是关于x的一元一次方程,则m的值是( )
A.±1 B.1 C.-1 D.0或1
分析:方程(m+1)x |m| +3=0是关于x的一元一次方程,则m+1≠0,|m|=1,所以m=1.答案:B
7. 方程 ,去分母,得( )
A.2x-1-x+1=6 B.3(2x-1)-2(x+1)=6
C.2(2x-1)-3(x+1)=6 D.3x-3-2x-2=1
分析:根据等式的基本性质:方程的两边同乘以6,方程的解不变.答案:B
B
B
考点对接
8. 如果5a 3 b 5(m-1)与a 3 b 6m-7 是同类项,那么m的值为( )
A.-4 B.2 C.-2 D.4
分析:根据同类项的定义,转化为方程.5(m-1)=6m-7,解得m=2.故选B. 答案:B
9.如果式子x+2与-2x+4的值是互为相反数,则x的值?
解:根据互为相反的两数之和等于0 可得
x+2+(-2x+4)=0
x+2-2x+4=0
-x+6=0
- x =-6
x =6 所以x的值为6
B
考点对接
10. 解方程:3(x+1)-(5+x)=18-2(x-1).
解:去括号,得3x+3-5-x=18-2x+2;
移项,得 3x-x+2x=18+2-3+5;
合并同类项,得 4x=22.
系数化为1,得 x= .
考点对接
12. 解方程:5x-|x|=8.
解:当x≥0时,原式化为
5x-x=8
4x=8
x=2
当x<0时,原式化为
5x-(-x)=8
6x=8
x= (不满足x<0的条件,所以不符合要求,应舍去)
方程的解为x=2
考点对接
13. 已知x 2m-3 +6=m是关于x的一元一次方程,试求代数式(m-3) 2 006 的值.
解:由已知x 2m-3 +6=m是关于x的一元一次方程,
得2m-3=1;
解之,得m=2;
从而(m-3) 2 006
=(2-3) 2 006
=(-1) 2 006 =1.
考点对接
(二)列一元一次方程解应用题
1.一般步骤
(1)审题,分析题中已知什么,未知什么,明确各量之间的关系,寻找等量关系;
(2)设未知数,一般求什么就设什么为x,但有时也可以间接设未知数;
(3)列方程,把相等关系左右两边的量用含有未知数的代数式表示出来,列出方程;
(4)解方程;
(5)检验,看该解是否是方程的解、是否符合题意.
(6)写出答案.
知识回顾
1. 要锻造一个直径为 8 cm 、高为 4 cm 的圆柱形毛坯,至少应截取直径为 4 cm 的圆钢的长度为( ).
A.6cm B.10cm C.16cm D. 20cm
分析:设圆钢为x cm,则π(2)2 x=π(4)2 ×4,
解得x=16. 答案:C
C
考点对接
2. 某商店在某一时间以每件50元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,在这次买卖中,该家商店( )
A.亏损6.7元 B.盈利6.7元 C.不亏不盈 D.以上都不正确
分析:设盈利25%的那件衣服的进价是x元,
根据进价与利润的和等于售价列得方程:x+0.25x=50,
解得:x=40,
类似地,设另一件亏损衣服的进价为y元,它的商品利润是-25%y元,
列方程y+(-25%y)=50,
解得:y=66.7.
那么这两件衣服的进价是x+y=106.7元,而两件衣服的售价为100元.
∴100-106.7=-6.7元,
所以,该家商店亏损6.7元.故选: A.
A
考点对接
3. 某人以八折的优惠价购买一套服装节省15元,那么这个人购买这套服装用去( )
A.35元 B.60元 C.75元 D.150元
4. 某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分加倍收费.某职工某月交水费16m元,则该职工这个月实际用水为( )
A.13立方米 B.14立方米 C.18立方米 D.26立方米
B
A
考点对接
5. 甲、乙两人从同一地点出发前往某地,若乙先走1小时,甲从后面追赶,当甲追上乙时,不成立的是( )
A.乙比甲先走1小时
B.甲、乙两人行程之和等于出发地和相遇地两点距离的2倍
C.乙走的路程比甲多 D.甲、乙两人所走的路程相等
6. 教室里有40套课桌椅,共计2 800元,每把椅子20元,问每张桌子多少元?设每张桌子x元,可列方程为( )
A.40x+20=2 800 B.40x+40×20=2 800
C.40x+20(40-x)=2 800 D.40(x-20)=2 800
C
B
考点对接
7. 小亮家今年承包的鱼塘到期了,共起出鲫鱼和鳊鱼500千克,共卖了2800元,已知鲫鱼和鳊鱼每千克分别为6元和5元,则鲫鱼和鳊鱼各千克.
解:设鲫鱼x千克,则鳊(500-x)千克,
由题意得 6x+5(500-x)=2800
解得x=300
则鳊(500-x)=500-300=200
答:鲫鱼300千克,鳊鱼200千克.
考点对接
8. A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x+80=240
解得 x=2
答:设B车行了2小时后与A车相距80千米。
考点对接
9.环湖一周800米,甲练习骑自行车平均每分钟行300米,乙练习跑步平均每分钟跑200米,两人同时同地出发.
(1)若两人背向而行,则他们经过多少时间首次相遇?
(2)若两人同向而行,则他们经过多少时间首次相遇?
解:(1)设相遇的时间为x,
根据题意就有500x+200x=800,
解得x≈1.143,故大约经过1.143分钟他们首次相遇.
(2)设相遇的时间为y,
根据题意就有500y-200y=800,
解得y≈2.67,故大约经过2.67分钟首次相遇.
考点对接
10. 某市居民生活用电基本价格为每度0.40元,若每月用电量超过a度,超出部分按基本电价的70%收费.
(1)某户五月份用电84度,共交电费30.72元,求a.
(2)若该户六月份的电费平均为每度0.36元,求六月份共用电多少度?应交电费多少元?
解:(1)由题意,有这样的相等关系:
a度电的电费+超出a度的那部分电费=五月份总电费,
由此得方程0.40a+(84-a)×0.40×70%=30.72,
解得a=60.
(2)设该户六月份共用电x度,由题意,有相等关系:
60度电的电费+超出60度的那部分电费=六月份总电费,
由此得方程0.40×60+(x-60)×0.40×70%=0.36x,
解得x=90,则0.36x=32.40.
答:该户六月份共用电90度,应交电费32.40元.
考点对接
11.北魏著名数学家张丘建撰写的《张丘建算经》:今有甲、乙怀银,不知其数,乙得甲十银,适等;甲得乙十银,多乙余钱5倍,问甲、乙怀银各几何?
分析:甲乙两人各有钱若干,若甲给乙十个钱,则两人的钱数刚好相等,则甲比乙多的钱,若乙给甲10个钱,甲是乙余下来的钱数多5倍;问:两人原来各有多少钱?
解:设甲怀银x枚,则乙怀银(x-20)枚,由题意得
x+10=6(x-20-10),
解得x=38,x-20=18 ,
答:甲怀银38枚,乙怀银18枚.
考点对接
1.下列方程是一元一次方程的是( )
A.x2=25 B.x-5=6 C. 3x-y=6 D. =2
2.若(m-1)x|m|+5=0是一元一次方程,则m的值为( )
A.1 B.-1 C.±1 D.不能确定
3.已知关于x的方程5x+3k=24与方程5x+3=0的解相同,则k的值是( )
A.7 B.-8 C.-10 D.9
B
B
D
随堂检测
4.解下列方程:
(1)2(x+3)=5(x-3); (2)
解:(1)2x+6=5x-15
-3x=-21
x=7
随堂检测
(2)10x-5=12-9x-15x
34x=17
x= .
5.已知关于x的方程 的解比方程5(x-1)-1=4(x-1)+1的解大2. (1)求第二个方程的解; (2)求m的值.
解:(1)5(x-1)-1=4(x-1)+1
5x-5-1=4x-4+1
5x-4x=-4+1+1+5
x=3.
(2)由题意得:方程 的解为x=3+2=5,
把x=5代入方程 ,得
,解得m=22.
随堂检测
6.甲、乙两人从A地出发前往B地,甲出发2小时后,乙开始出发,已知甲的速度是15 km/h,乙的速度是60 km/h,A,B两地相距100 km,乙追上甲的地方离B地多远?
解:设乙出发x h后追上甲,则此时甲出发了(x+2)h.
根据题意,得60x=15(x+2),
解得x=23 ,
∴100-60x=100-60×23=60.
则乙追上甲的地方离B地60 km.
?
随堂检测
7.整理一批图书,由一个人做要40小时完成.现计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
解:设应先安排x人工作.
根据题意,得 ,
化简可得 x+2(x+2)=10,
解得x=2,
则应先安排2人工作.
随堂检测
8.入冬以来,某家电销售部以150元/台的价格购进一款烤火器,很快售完,又用相同的货款再次购进这款烤火器.因单价提高了30元,进货量比第一次少了10台.
(1)家电销售部两次各购进烤火器多少台?
(2)若以250元/台的售价卖完这两批烤火器,家电销售部共获利多少元?
解:(1)设第一次购进烤火器x台,则第二次购进烤火器(x-10)台.
根据题意得150x=180(x-10),
解得x=60,x-10=50.
则家电销售部第一次购进烤火器60台,第二次购进50台.
(2)(250-150)×60+(250-180)×50=9 500(元).
故家电销售部共获利9 500元.
随堂检测
9.甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物x元(x>300).
(1)请用含x代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
解:(1)设顾客在甲超市购物所付的费用为y甲,顾客在乙超市购物所付的费用为y乙,
根据题意得y甲=300+0.8(x-300)=0.8x+60;y乙=200+0.85(x-200)=0.85x+30.
(2)他应该去乙超市,理由如下:当x=500时,y甲=0.8x+60=460,y乙=0.85x+30=455,
∵460>455,∴他去乙超市划算.
(3)令y甲=y乙,即0.8x+60=0.85x+30,解得x=600.
则李明购买600元的商品时,到两家超市购物所付的费用一样.
随堂检测
10.请根据图中提供的信息,回答下列问题:
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算?并说明理由.(必须在同一家购买)
解:(1)设一个水瓶x元,表示出一个水杯为(48-x)元.根据题意得
3x+4(48-x)=152,解得x=40,
则一个水瓶是40元,一个水杯是8元.
(2)甲商场所需费用为(40×5+8×20)×80%=288(元).
乙商场所需费用为5×40+(20-5×2)×8=280(元).
∵288>280,∴选择乙商场购买更合算.
随堂检测
本章知识重点
1.一元一次方程
2.解一元一次方程
3.一元一次方程的应用
温馨提示
1.化简后分母中含有未知数的方程不是一元一次方程
2.去分母时不要漏乘不含分母的项
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
