北师大版七年级数学上册第5章第6节应用一元一次方程——追赶小明 (2)(共33张PPT)
文档属性
| 名称 | 北师大版七年级数学上册第5章第6节应用一元一次方程——追赶小明 (2)(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:34:16 | ||
图片预览







文档简介
焦老 站在甲、乙两地之间的某个位置,他想乘坐出租车到乙地去。他看见一辆空车远远地从甲地驶来,而此时整条路上并没有别人与他争抢空车。我们假定车的行驶速度和人的步行速度都是固定不变的,并且车速大于人速。为了更快地到达目的地,焦老 应该怎样做呢?你认为下面哪种思路是正确的?
(A) 由于车速大于人速,焦老 应该尽可能早地上车,充分利用汽车的速度优势。因此,焦老 应该迎着空车走上去,提前与车相遇。
(B) 为了尽早到达目的地,焦老 应该充分利用时间,马不停蹄地赶往目的地。因此,他应该自己先朝目的地走一段路,再让出租车载他走完剩下的路程。
其实两种方案花费的时间是一样的。只要站在出租车的角度上想一想,问题就变得很显然了:不管焦老 在哪儿上车,出租车都要驶完甲地到乙地的全部路程,因此焦老 到达乙地的时间总等于出租车驶完全程的时间,加上途中接焦老上车可能耽误的时间。
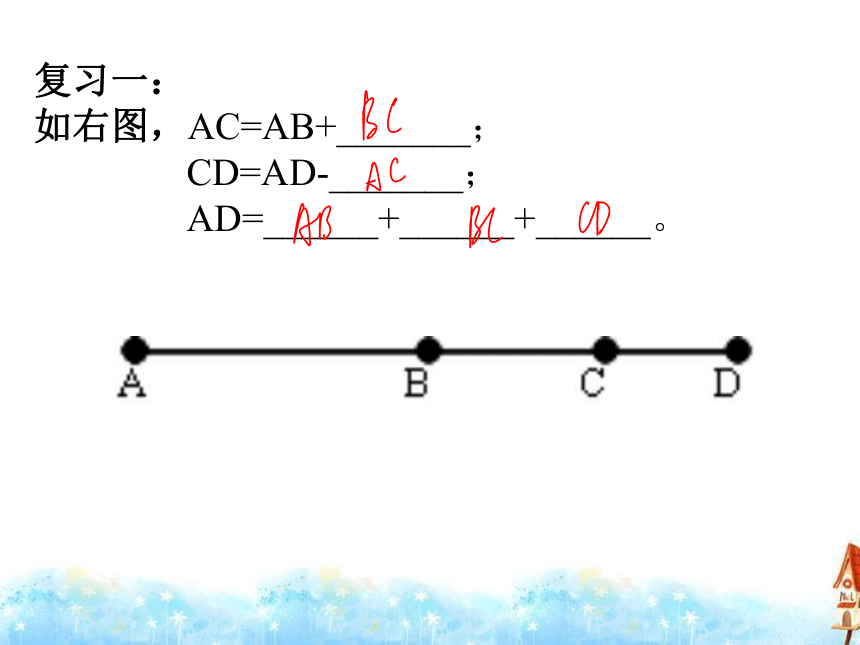
复习一:
如右图,AC=AB+_______;
CD=AD-_______;
AD=______+______+______。
1.若小明每分跑200米,那么他5分钟能跑_____米.
1000
S=v t
路程=速度 X 时间
复习二
2.小明用10分钟绕学校操场跑了六圈(每圈400米),那么他的速度为_____米/分.
速度=路程÷时间
v=
240
S
t
3.已知小明家距离学校1000米,他以250米/分的速度骑车到达学校需要____分。
t=
4
S
V
小明爸爸和小明每天早晨坚持跑步,小明爸爸每秒跑6米,小明每秒跑4米。
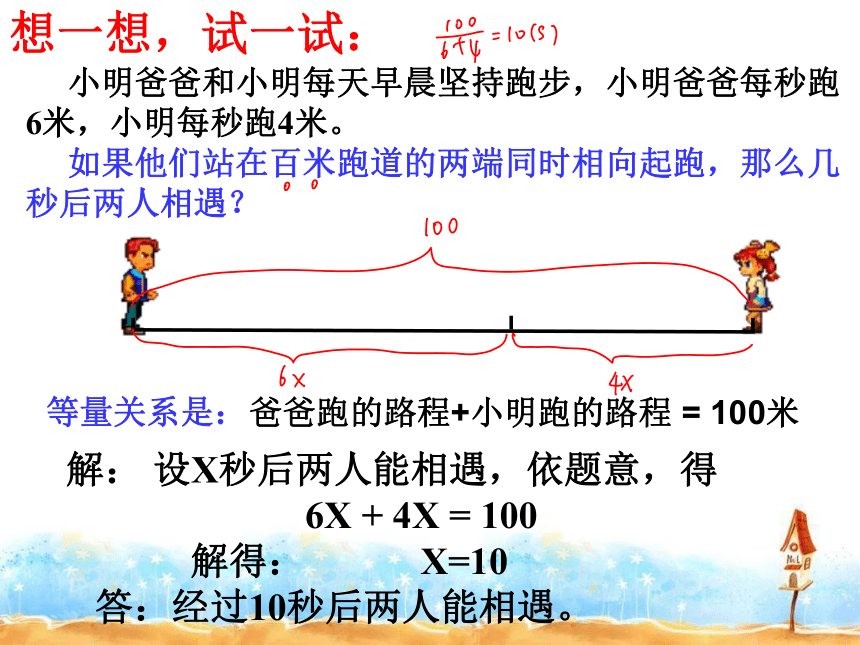
如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
等量关系是:
爸爸跑的路程+小明跑的路程 = 100米
解: 设X秒后两人能相遇,依题意,得
6X + 4X = 100
解得: X=10
答:经过10秒后两人能相遇。
想一想,试一试:
小明爸爸和小明每天早晨坚持跑步,小明爸爸每秒跑6米,小明每秒跑4米。
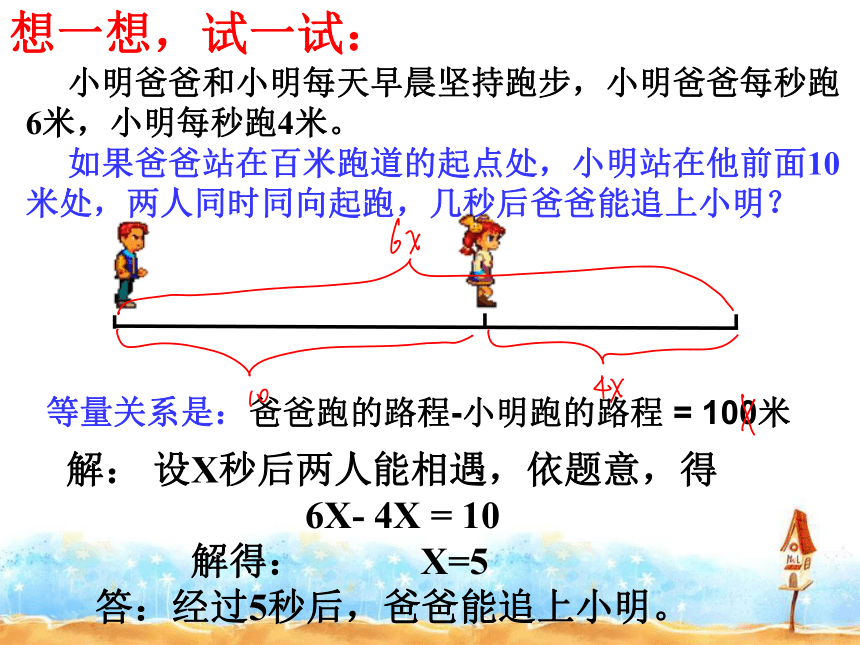
如果爸爸站在百米跑道的起点处,小明站在他前面10米处,两人同时同向起跑,几秒后爸爸能追上小明?
等量关系是:
爸爸跑的路程-小明跑的路程 = 100米
解: 设X秒后两人能相遇,依题意,得
6X- 4X = 10
解得: X=5
答:经过5秒后,爸爸能追上小明。
想一想,试一试:
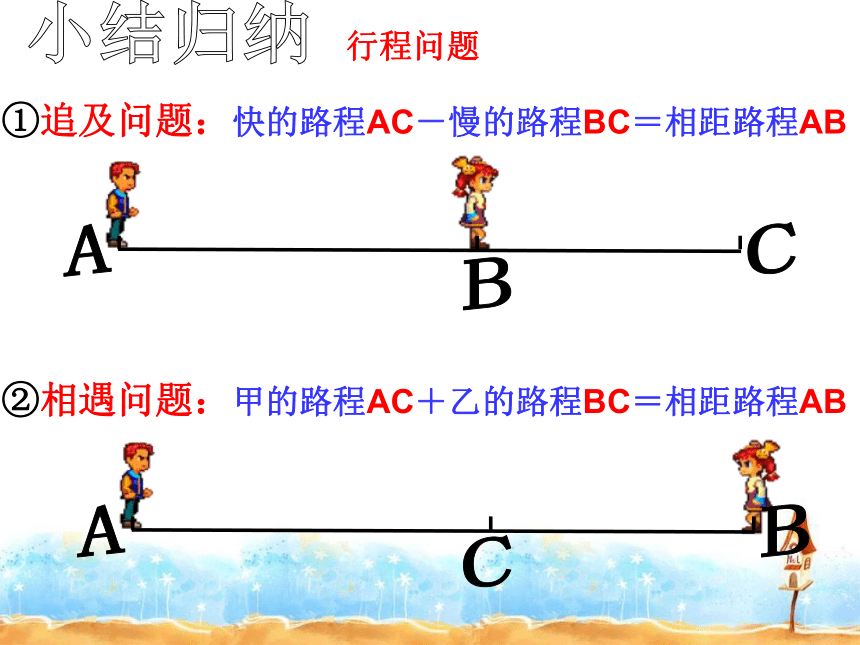
①追及问题:快的路程AC-慢的路程BC=相距路程AB
②相遇问题:甲的路程AC+乙的路程BC=相距路程AB
行程问题
解决路程问题的关键是什么?
找出等量关系的重要方法是:
找出等量关系,列出方程。
画线段图。
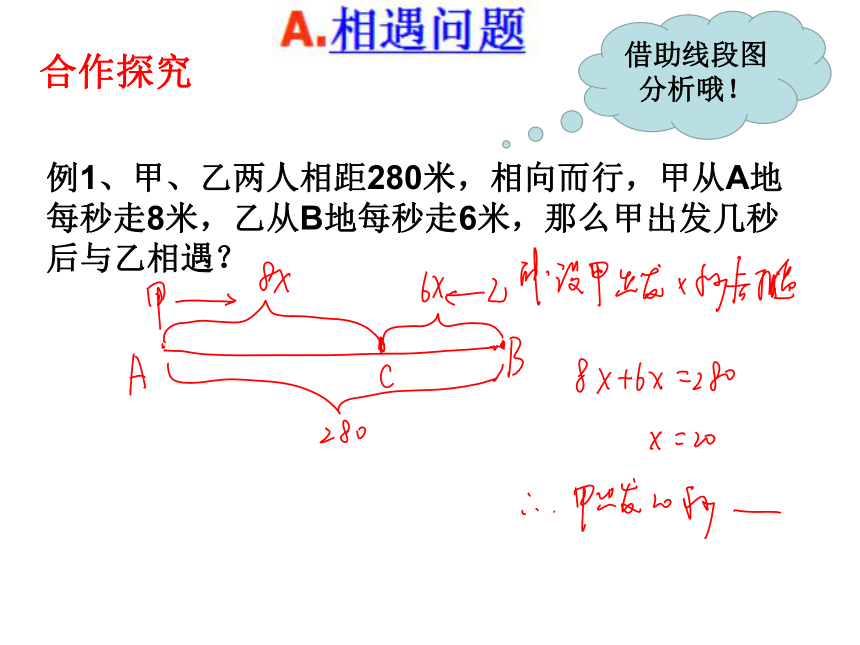
合作探究
例1、甲、乙两人相距280米,相向而行,甲从A地每秒走8米,乙从B地每秒走6米,那么甲出发几秒后与乙相遇?
借助线段图分析哦!
例2:400米的环形跑道上,甲练习骑自行车,速度为6米/秒,乙练习跑步,速度为4米/秒,若两人同时同地相向而行,多少秒后两人首次相遇?
例1:小明每天早上要在7:50之前赶到距家1000米的学校上学。
爸爸能追上小明吗?
一天小明以80米/分的速度出发,5分后,小明的爸爸发现他忘带语文书。于是爸爸立即以180米/分的速度去追小明。
1. 小明前5分钟的行程+小明被追上的行程=爸爸的行程
2.小明被追上所用的时间=爸爸追上小明所用的时间
180x
80×5
80x
等量关系:
例1:小明每天早上要在7:50之前赶到距家1000米的学校上学。
一天小明以80米/分的速度出发,5分后,小明的爸爸发现他忘带语文书。于是爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
(2)追上小明时,距离学校还有多远?
小明每天早上要在7:50之前赶到距家1000米的学校上学。一天小明以80米/分的速度出发5分后,小明的爸爸发现他忘了带语文书。于是他爸爸立即以180米/分的速度去追小明,此时,小明也发现自己的忘了带语文书,也立即以80米/分的速度返回。
问:过了多长时间小明和爸爸相遇?
例题延伸
1、A、B两地相距480千米,一列慢车从A地出发,每小时行60千米,一列快车从B地开出,每小时行65千米。
(1)两车同时开出,相向而行,x小时相遇,则由条件可列方程为 。
(2)若两车都从A站出发,同向而行,慢车先行40千米,快车从A站出发,x小时追上慢车,则由条件可列方程为 。
(3)若两车都从A站出发,同向而行,慢车先行半小时,快车从A站出发,x小时追上慢车,则
由条件可列方程为 。
当 堂 训 练
60x+65x=480
65x-60x=40
65x-60x=30
当 堂 训 练
2、一个自行车队进行训练,训练时所有队员都以35千米/时的速度前进,突然,1号队员以45千米/时的速度独自行进,行进10千米后掉转车头,仍以45千米/时的速度往回骑,直到与其他队员会合。1号队员从离队开始到与队员重新会合,经过了多长时间?
练习:甲乙两人相距40千米,甲在后乙在前,两人同向而行,甲先出发1.5小时后乙再出发,甲的速度为每小时8千米,乙的速度为每小时6千米,甲出发几小时后追上乙?
甲
乙
40千米
育红学校七年级学生步行到郊外旅行。(1)班的学生组成前队,步行速度为4千米/时,(2)班的学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
议一议:
根据上面的事实提出问题并尝试去解答.
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
问题4:当后队追上前队时,前、后队行走了多少路程?
问题5:联络员在前队出发多少时间后第一次追上前队?
问题1:后队追上前队用了多长时间 ?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设后队追上前队用了x小时,由题意
列方程得:
6x = 4x + 4
解方程得:x =2
答:后队追上前队时用了2小时。
问题2:后队追上前队时联络员行了多少路程?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:由问题1得后队追上前队用了2小时,因此
联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
问题3:联络员第一次追上前队时用了多长时间?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设联络员第一次追上前队时用了x小时,
由题意列方程得;
12x = 4x + 4
解方程得:x =0.5
答:联络员第一次追上前队时用了0.5小时。
问题4:当后队追上前队时,他们已经行进了多少路程?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设当后队追上前队时,他们已经行进了x千米,
由题意列方程得:
解得; x = 12
答:当后队追上前队时,他们已经行进12千米.
问题5:联络员在前队出发多少时间后第一次追上前队?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设联络员在前队出发x小时后第一次追上前队,
由题意列方程得;
答:联络员在前队出发后1.5 小时后第一次追上前队.
4x = 12(x - 1)
解方程得: x = 1.5
练习:甲、乙二人绕学校操场400米的环形跑道跑步,甲每秒跑8米,乙每秒跑6米,如果两人同时同地同向而行,甲第一次超过乙用时多长?
例 甲、乙两人在400米的环形跑道上散步,甲每分钟走110米,乙每分钟走90米,两人同时从一个地点出发,几分钟后两人第一次相遇?
分析:在环形跑道上运动,分两种情况:
已知:V甲>V乙
图一所示实为 问题
图二所示实为 问题
相遇
追击
乙
甲
乙
甲
环形跑道问题
环形跑道问题
例 甲、乙两人在400米的环形跑道上散步,甲每分钟走110米,乙每分钟走90米,两人同时从一个地点出发,几分钟后两人第一次相遇。
分析:在环形跑道上运动,分两种情况:
甲的行程+乙的行程=跑道一圈的周长
(2)同向而行:
甲的行程-乙的行程=跑道一圈的周长
想一想 若把上题中的“第一次”相遇改为“第二次”
相遇需要时间又是多少呢?若改为“第n次”相遇呢?
(1)背向而行:
(1)解应用题(特别是运动问题)要学会借助线段图来分析数量关系;
(2)学会文字语言、图形语言、符号语言的互相渗透,互相转换。
(1)从时间考虑:
速度慢的用时-速度快的用时=多用的时间
(2)从路程考虑:
速度快的行程-速度慢的行程=两者的距离
一、行程问题中的基本等量关系为:
路程=速度×时间
二、一般可从下面两个方面寻找追及问题中的等量关系:
三、解决路程问题的关键是… …,方法是……
课堂小结
作业:
1.题单
2.电子作业
(A) 由于车速大于人速,焦老 应该尽可能早地上车,充分利用汽车的速度优势。因此,焦老 应该迎着空车走上去,提前与车相遇。
(B) 为了尽早到达目的地,焦老 应该充分利用时间,马不停蹄地赶往目的地。因此,他应该自己先朝目的地走一段路,再让出租车载他走完剩下的路程。
其实两种方案花费的时间是一样的。只要站在出租车的角度上想一想,问题就变得很显然了:不管焦老 在哪儿上车,出租车都要驶完甲地到乙地的全部路程,因此焦老 到达乙地的时间总等于出租车驶完全程的时间,加上途中接焦老上车可能耽误的时间。
复习一:
如右图,AC=AB+_______;
CD=AD-_______;
AD=______+______+______。
1.若小明每分跑200米,那么他5分钟能跑_____米.
1000
S=v t
路程=速度 X 时间
复习二
2.小明用10分钟绕学校操场跑了六圈(每圈400米),那么他的速度为_____米/分.
速度=路程÷时间
v=
240
S
t
3.已知小明家距离学校1000米,他以250米/分的速度骑车到达学校需要____分。
t=
4
S
V
小明爸爸和小明每天早晨坚持跑步,小明爸爸每秒跑6米,小明每秒跑4米。
如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
等量关系是:
爸爸跑的路程+小明跑的路程 = 100米
解: 设X秒后两人能相遇,依题意,得
6X + 4X = 100
解得: X=10
答:经过10秒后两人能相遇。
想一想,试一试:
小明爸爸和小明每天早晨坚持跑步,小明爸爸每秒跑6米,小明每秒跑4米。
如果爸爸站在百米跑道的起点处,小明站在他前面10米处,两人同时同向起跑,几秒后爸爸能追上小明?
等量关系是:
爸爸跑的路程-小明跑的路程 = 100米
解: 设X秒后两人能相遇,依题意,得
6X- 4X = 10
解得: X=5
答:经过5秒后,爸爸能追上小明。
想一想,试一试:
①追及问题:快的路程AC-慢的路程BC=相距路程AB
②相遇问题:甲的路程AC+乙的路程BC=相距路程AB
行程问题
解决路程问题的关键是什么?
找出等量关系的重要方法是:
找出等量关系,列出方程。
画线段图。
合作探究
例1、甲、乙两人相距280米,相向而行,甲从A地每秒走8米,乙从B地每秒走6米,那么甲出发几秒后与乙相遇?
借助线段图分析哦!
例2:400米的环形跑道上,甲练习骑自行车,速度为6米/秒,乙练习跑步,速度为4米/秒,若两人同时同地相向而行,多少秒后两人首次相遇?
例1:小明每天早上要在7:50之前赶到距家1000米的学校上学。
爸爸能追上小明吗?
一天小明以80米/分的速度出发,5分后,小明的爸爸发现他忘带语文书。于是爸爸立即以180米/分的速度去追小明。
1. 小明前5分钟的行程+小明被追上的行程=爸爸的行程
2.小明被追上所用的时间=爸爸追上小明所用的时间
180x
80×5
80x
等量关系:
例1:小明每天早上要在7:50之前赶到距家1000米的学校上学。
一天小明以80米/分的速度出发,5分后,小明的爸爸发现他忘带语文书。于是爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
(2)追上小明时,距离学校还有多远?
小明每天早上要在7:50之前赶到距家1000米的学校上学。一天小明以80米/分的速度出发5分后,小明的爸爸发现他忘了带语文书。于是他爸爸立即以180米/分的速度去追小明,此时,小明也发现自己的忘了带语文书,也立即以80米/分的速度返回。
问:过了多长时间小明和爸爸相遇?
例题延伸
1、A、B两地相距480千米,一列慢车从A地出发,每小时行60千米,一列快车从B地开出,每小时行65千米。
(1)两车同时开出,相向而行,x小时相遇,则由条件可列方程为 。
(2)若两车都从A站出发,同向而行,慢车先行40千米,快车从A站出发,x小时追上慢车,则由条件可列方程为 。
(3)若两车都从A站出发,同向而行,慢车先行半小时,快车从A站出发,x小时追上慢车,则
由条件可列方程为 。
当 堂 训 练
60x+65x=480
65x-60x=40
65x-60x=30
当 堂 训 练
2、一个自行车队进行训练,训练时所有队员都以35千米/时的速度前进,突然,1号队员以45千米/时的速度独自行进,行进10千米后掉转车头,仍以45千米/时的速度往回骑,直到与其他队员会合。1号队员从离队开始到与队员重新会合,经过了多长时间?
练习:甲乙两人相距40千米,甲在后乙在前,两人同向而行,甲先出发1.5小时后乙再出发,甲的速度为每小时8千米,乙的速度为每小时6千米,甲出发几小时后追上乙?
甲
乙
40千米
育红学校七年级学生步行到郊外旅行。(1)班的学生组成前队,步行速度为4千米/时,(2)班的学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
议一议:
根据上面的事实提出问题并尝试去解答.
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
问题4:当后队追上前队时,前、后队行走了多少路程?
问题5:联络员在前队出发多少时间后第一次追上前队?
问题1:后队追上前队用了多长时间 ?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设后队追上前队用了x小时,由题意
列方程得:
6x = 4x + 4
解方程得:x =2
答:后队追上前队时用了2小时。
问题2:后队追上前队时联络员行了多少路程?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:由问题1得后队追上前队用了2小时,因此
联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
问题3:联络员第一次追上前队时用了多长时间?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设联络员第一次追上前队时用了x小时,
由题意列方程得;
12x = 4x + 4
解方程得:x =0.5
答:联络员第一次追上前队时用了0.5小时。
问题4:当后队追上前队时,他们已经行进了多少路程?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设当后队追上前队时,他们已经行进了x千米,
由题意列方程得:
解得; x = 12
答:当后队追上前队时,他们已经行进12千米.
问题5:联络员在前队出发多少时间后第一次追上前队?
育红学校七年级学生步行到郊外旅行,1班的学生组成
前队,步行的速度为4千米/小时,2班的学生组成后队,
速度为6千米/小时,前队出发1小时后,后队出发,
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络,他骑车的速度为12千米 /小时。
解:设联络员在前队出发x小时后第一次追上前队,
由题意列方程得;
答:联络员在前队出发后1.5 小时后第一次追上前队.
4x = 12(x - 1)
解方程得: x = 1.5
练习:甲、乙二人绕学校操场400米的环形跑道跑步,甲每秒跑8米,乙每秒跑6米,如果两人同时同地同向而行,甲第一次超过乙用时多长?
例 甲、乙两人在400米的环形跑道上散步,甲每分钟走110米,乙每分钟走90米,两人同时从一个地点出发,几分钟后两人第一次相遇?
分析:在环形跑道上运动,分两种情况:
已知:V甲>V乙
图一所示实为 问题
图二所示实为 问题
相遇
追击
乙
甲
乙
甲
环形跑道问题
环形跑道问题
例 甲、乙两人在400米的环形跑道上散步,甲每分钟走110米,乙每分钟走90米,两人同时从一个地点出发,几分钟后两人第一次相遇。
分析:在环形跑道上运动,分两种情况:
甲的行程+乙的行程=跑道一圈的周长
(2)同向而行:
甲的行程-乙的行程=跑道一圈的周长
想一想 若把上题中的“第一次”相遇改为“第二次”
相遇需要时间又是多少呢?若改为“第n次”相遇呢?
(1)背向而行:
(1)解应用题(特别是运动问题)要学会借助线段图来分析数量关系;
(2)学会文字语言、图形语言、符号语言的互相渗透,互相转换。
(1)从时间考虑:
速度慢的用时-速度快的用时=多用的时间
(2)从路程考虑:
速度快的行程-速度慢的行程=两者的距离
一、行程问题中的基本等量关系为:
路程=速度×时间
二、一般可从下面两个方面寻找追及问题中的等量关系:
三、解决路程问题的关键是… …,方法是……
课堂小结
作业:
1.题单
2.电子作业
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
