27.2.3相似三角形应用举例-人教版九年级数学下册20分钟课后精华同步轻松练(Word版 含解析)
文档属性
| 名称 | 27.2.3相似三角形应用举例-人教版九年级数学下册20分钟课后精华同步轻松练(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 263.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:00:00 | ||
图片预览




文档简介
27.2.3相似三角形应用举例
一.选择题(共6小题)
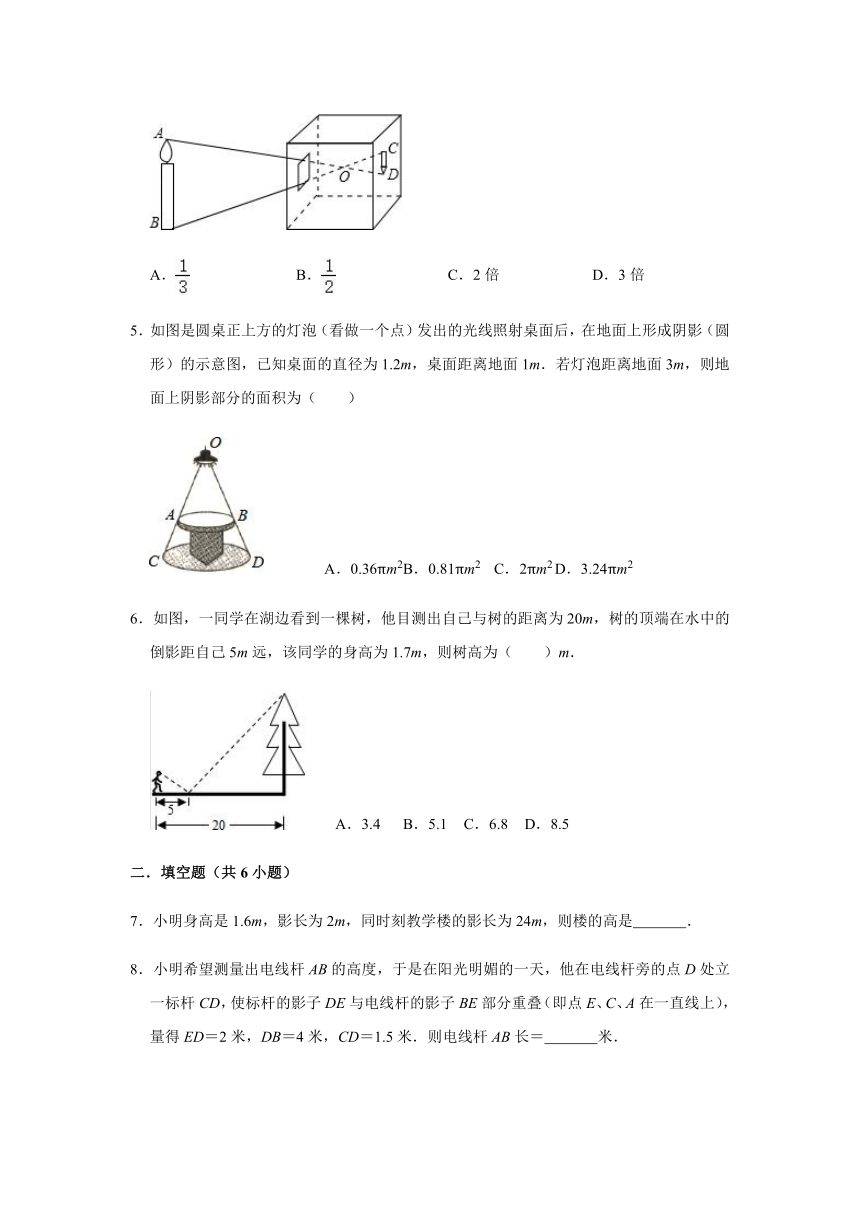
1.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米
B.米
C.36米
D.米
2.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm
B.20cm
C.25cm
D.30cm
3.如图有一块四边形草地ABCD,AD∥BC,其中AB=4,BC=5,由于连续降雨使AD间积满污水,现在BA、CD的延长线的交点P处测得PA=3,则AD的长度为( )
A.2
B.
C.
D.
4.在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A.
B.
C.2倍
D.3倍
5.如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2
B.0.81πm2
C.2πm2
D.3.24πm2
6.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4
B.5.1
C.6.8
D.8.5
二.填空题(共6小题)
7.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是
.
8.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米.则电线杆AB长=
米.
9.根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表.如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是
.
10.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米,某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),则这个矩形的面积是
平方米.
11.比例规是一种画图工具,利用它可以把线段按一定比例伸长或缩短.它是由长短相等的两脚AD和BC交叉构成的,其中AD与BC相交于点O.如图,OA=OB,CD=2,AB=2CD,OC=3,则OB=
.
12.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB=
米.
三.解答题(共3小题)
13.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
14.如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)
15.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
27.2.3相似三角形应用举例
参考答案与试题解析
一.选择题(共6小题)
1.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米
B.米
C.36米
D.米
【解答】解:∵BC⊥CA,MN⊥AN,
∴∠C=∠MNA=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴=,
即=,
∴MN=32(m),
答:楼房MN的高度为32m.
故选:A.
2.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm
B.20cm
C.25cm
D.30cm
【解答】解:∵AB∥DE,
∴△CAB∽△CDE,
∴=,
而BC=BE,
∴DE=2AB=2×15=30(cm).
故选:D.
3.如图有一块四边形草地ABCD,AD∥BC,其中AB=4,BC=5,由于连续降雨使AD间积满污水,现在BA、CD的延长线的交点P处测得PA=3,则AD的长度为( )
A.2
B.
C.
D.
【解答】解:∵四边形ABCD中,AD∥BC,
∴△PAD∽△PBC,
∴PA:PB=AD:BC,
∵PA=3,AB=4,BC=5,
∴3:7=AD:5,
解得:AD=,
故选:C.
4.在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A.
B.
C.2倍
D.3倍
【解答】解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴===(相似三角形的对应高的比等于相似比),
∴CD=AB,
故选:A.
5.如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2
B.0.81πm2
C.2πm2
D.3.24πm2
【解答】解:构造几何模型如图:
依题意知DE=1.2米,FG=1米,AG=3米,
由△DAE∽△BAC得=,即=,
得BC=1.8,
故S圆=(BC)2?π=()2?π=0.81π,
故选:B.
6.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4
B.5.1
C.6.8
D.8.5
【解答】解:由相似三角形的性质,设树高x米,
则=,
∴x=5.1m.
故选:B.
二.填空题(共6小题)
7.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是 19.2m .
【解答】解:设教学楼高度为xm,
列方程得:
解得x=19.2,
故教学楼的高度为19.2m.
故答案为:19.2m.
8.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米.则电线杆AB长= 4.5 米.
【解答】解:∵CD∥AB,
∴△ECD∽△EAB,
∴ED:EB=CD:AB,
∴2:6=1.5:AB,
∴AB=4.5米.
答:电线杆AB长为4.5米.
9.根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表.如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是 2.16 .
【解答】解:根据题意得=,
所以b=×3.6=2.16(cm).
故答案为2.16.
10.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米,某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),则这个矩形的面积是 2000 平方米.
【解答】解:由已知得,DG∥BC
∴△ADG∽△ABC,
∵AH⊥BC
∴AH⊥DG于点M
且AM=AH﹣MH=80﹣40=40(m)
,
即DG==50(m),
∴S矩形DEFG=DE×DG=2000(m2).
故答案为:2000.
11.比例规是一种画图工具,利用它可以把线段按一定比例伸长或缩短.它是由长短相等的两脚AD和BC交叉构成的,其中AD与BC相交于点O.如图,OA=OB,CD=2,AB=2CD,OC=3,则OB= 6 .
【解答】解:由题意得:△AOB∽△DOC,
∵AB=2CD,
∴,
∴==,
∵CD=2,OC=3,
∴OB=2OC=6,
故答案为:6.
12.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB= 6 米.
【解答】解:根据题意可得:
∠AEB=∠CED,∠BAE=∠DCE=90°,
∴△ABE∽△CDE,
∴=,
∴,
∴AB=6(米),
故答案为:6.
三.解答题(共3小题)
13.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
【解答】(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴=,
设FC=xcm,则=,
解得:x=160,
答:CF的长为160cm.
14.如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)
【解答】解:设AE=x,∵CD∥AE,
∴△CDF∽△AFB,
∴,即,
∴FC=,
∵CD∥AB,
∴△GCD∽△GAE,
∴,即=,
解得:x=40,(负值舍去),
∴AE=40,
∴大厦主体建筑的高度是40米.
15.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
【解答】解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米.
一.选择题(共6小题)
1.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米
B.米
C.36米
D.米
2.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm
B.20cm
C.25cm
D.30cm
3.如图有一块四边形草地ABCD,AD∥BC,其中AB=4,BC=5,由于连续降雨使AD间积满污水,现在BA、CD的延长线的交点P处测得PA=3,则AD的长度为( )
A.2
B.
C.
D.
4.在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A.
B.
C.2倍
D.3倍
5.如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2
B.0.81πm2
C.2πm2
D.3.24πm2
6.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4
B.5.1
C.6.8
D.8.5
二.填空题(共6小题)
7.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是
.
8.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米.则电线杆AB长=
米.
9.根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表.如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是
.
10.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米,某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),则这个矩形的面积是
平方米.
11.比例规是一种画图工具,利用它可以把线段按一定比例伸长或缩短.它是由长短相等的两脚AD和BC交叉构成的,其中AD与BC相交于点O.如图,OA=OB,CD=2,AB=2CD,OC=3,则OB=
.
12.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB=
米.
三.解答题(共3小题)
13.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
14.如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)
15.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
27.2.3相似三角形应用举例
参考答案与试题解析
一.选择题(共6小题)
1.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米
B.米
C.36米
D.米
【解答】解:∵BC⊥CA,MN⊥AN,
∴∠C=∠MNA=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴=,
即=,
∴MN=32(m),
答:楼房MN的高度为32m.
故选:A.
2.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm
B.20cm
C.25cm
D.30cm
【解答】解:∵AB∥DE,
∴△CAB∽△CDE,
∴=,
而BC=BE,
∴DE=2AB=2×15=30(cm).
故选:D.
3.如图有一块四边形草地ABCD,AD∥BC,其中AB=4,BC=5,由于连续降雨使AD间积满污水,现在BA、CD的延长线的交点P处测得PA=3,则AD的长度为( )
A.2
B.
C.
D.
【解答】解:∵四边形ABCD中,AD∥BC,
∴△PAD∽△PBC,
∴PA:PB=AD:BC,
∵PA=3,AB=4,BC=5,
∴3:7=AD:5,
解得:AD=,
故选:C.
4.在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A.
B.
C.2倍
D.3倍
【解答】解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴===(相似三角形的对应高的比等于相似比),
∴CD=AB,
故选:A.
5.如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2
B.0.81πm2
C.2πm2
D.3.24πm2
【解答】解:构造几何模型如图:
依题意知DE=1.2米,FG=1米,AG=3米,
由△DAE∽△BAC得=,即=,
得BC=1.8,
故S圆=(BC)2?π=()2?π=0.81π,
故选:B.
6.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4
B.5.1
C.6.8
D.8.5
【解答】解:由相似三角形的性质,设树高x米,
则=,
∴x=5.1m.
故选:B.
二.填空题(共6小题)
7.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是 19.2m .
【解答】解:设教学楼高度为xm,
列方程得:
解得x=19.2,
故教学楼的高度为19.2m.
故答案为:19.2m.
8.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米.则电线杆AB长= 4.5 米.
【解答】解:∵CD∥AB,
∴△ECD∽△EAB,
∴ED:EB=CD:AB,
∴2:6=1.5:AB,
∴AB=4.5米.
答:电线杆AB长为4.5米.
9.根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表.如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是 2.16 .
【解答】解:根据题意得=,
所以b=×3.6=2.16(cm).
故答案为2.16.
10.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米,某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),则这个矩形的面积是 2000 平方米.
【解答】解:由已知得,DG∥BC
∴△ADG∽△ABC,
∵AH⊥BC
∴AH⊥DG于点M
且AM=AH﹣MH=80﹣40=40(m)
,
即DG==50(m),
∴S矩形DEFG=DE×DG=2000(m2).
故答案为:2000.
11.比例规是一种画图工具,利用它可以把线段按一定比例伸长或缩短.它是由长短相等的两脚AD和BC交叉构成的,其中AD与BC相交于点O.如图,OA=OB,CD=2,AB=2CD,OC=3,则OB= 6 .
【解答】解:由题意得:△AOB∽△DOC,
∵AB=2CD,
∴,
∴==,
∵CD=2,OC=3,
∴OB=2OC=6,
故答案为:6.
12.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB= 6 米.
【解答】解:根据题意可得:
∠AEB=∠CED,∠BAE=∠DCE=90°,
∴△ABE∽△CDE,
∴=,
∴,
∴AB=6(米),
故答案为:6.
三.解答题(共3小题)
13.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
【解答】(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴=,
设FC=xcm,则=,
解得:x=160,
答:CF的长为160cm.
14.如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)
【解答】解:设AE=x,∵CD∥AE,
∴△CDF∽△AFB,
∴,即,
∴FC=,
∵CD∥AB,
∴△GCD∽△GAE,
∴,即=,
解得:x=40,(负值舍去),
∴AE=40,
∴大厦主体建筑的高度是40米.
15.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
【解答】解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米.
