沪教版数学七年级上册【9.5因式分解】专项巩固训练(word版含答案)
文档属性
| 名称 | 沪教版数学七年级上册【9.5因式分解】专项巩固训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 54.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 09:26:20 | ||
图片预览




文档简介
【因式分解】专项巩固训练
一.选择题
1.4x2y和6xy3的公因式是( )
A.2xy
B.3xy
C.2x2y
D.3xy3
2.多项式①2x2﹣x;②x2+4+4x;③x2+x﹣2;④﹣x2+4x﹣4,在分解因式结果含有相同因式的是( )
A.①和②
B.①和④
C.②和③
D.③和④
3.下列多项式中,能用平方差公式进行因式分解的是( )
A.a2﹣b2
B.﹣a2﹣b2
C.a2+b2
D.a2+2ab+b2
4.若x2+mx+9=(x+3)2,则m的值是( )
A.﹣18
B.18
C.﹣6
D.6
5.分解因式:4﹣12(a﹣b)+9(a﹣b)2=( )
A.(2+3a﹣3b)2
B.(2﹣3a﹣3b)2
C.(2+3a+3b)2
D.(2﹣3a+3b)2
6.下列四个等式从左到右的变形是因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.ab﹣a2=a(b﹣a)
C.x2+x﹣5=x(x+1)﹣5
D.x2+1=x(x+)
7.小明是一位密码翻译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:蜀、爱、我、巴、丽、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.我爱美
B.巴蜀美
C.我爱巴蜀
D.巴蜀美丽
8.已知m2=4n+a,n2=4m+a,m≠n,则m2+2mn+n2的值为( )
A.16
B.12
C.10
D.无法确定
9.二次三项式x2﹣mx﹣12(m是整数),在整数范围内可分为两个一次因式的积,则m的所有可能值有( )个.
A.4
B.5
C.6
D.8
10.已知664﹣1能被30﹣40之间的两个整数整除,则这两个整数是( )
A.35,37
B.35,36
C.34,38
D.36,37
二.填空题
11.因式分解3xy﹣6y=
.
12.已知m是常数,若x﹣3是2x2+mx+15的一个因式,则m的值为
.
13.如果关于x的二次三项式x2﹣4x+m在实数范围内不能分解因式,那么m的取值范围是
.
14.因式分解:x2﹣5x﹣36=
.
15.分解因式:b4﹣b2﹣12=
.
三.解答题
16.因式分解:
(1)x2+2x﹣15.
(2)3x2y2z﹣27y4z.
(3)(a2+1)2﹣4a2.
17.对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.
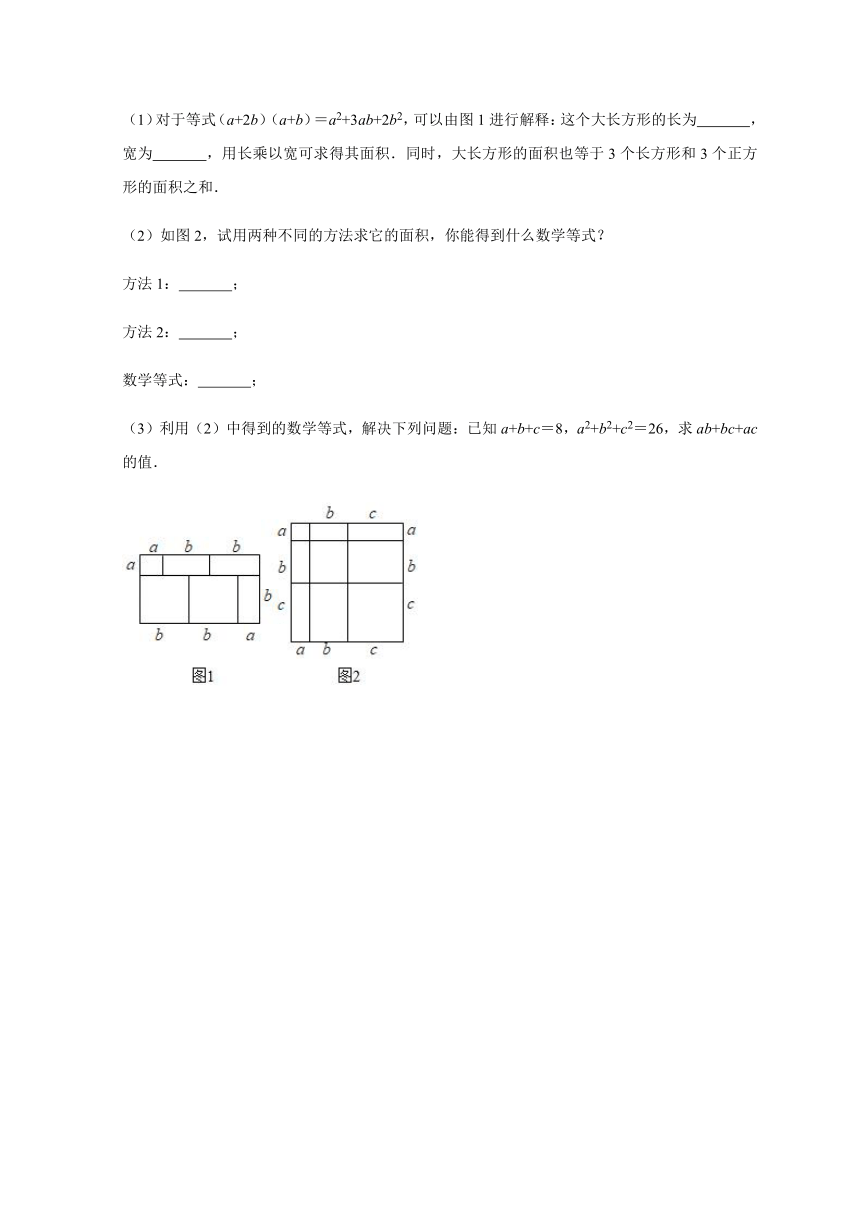
(1)对于等式(a+2b)(a+b)=a2+3ab+2b2,可以由图1进行解释:这个大长方形的长为
,宽为
,用长乘以宽可求得其面积.同时,大长方形的面积也等于3个长方形和3个正方形的面积之和.
(2)如图2,试用两种不同的方法求它的面积,你能得到什么数学等式?
方法1:
;
方法2:
;
数学等式:
;
(3)利用(2)中得到的数学等式,解决下列问题:已知a+b+c=8,a2+b2+c2=26,求ab+bc+ac的值.
18.观察下列关于自然数的等式:
a1:32﹣12=8×1;
a2:52﹣32=8×2;
a3:72﹣52=8×3;…
根据上述规律解决下列问题:
(1)写出第a4个等式:
;
(2)写出你猜想的第an个等式(用含n的式子表示),并验证其正确性;
(3)对于正整数k,若ak,ak+1,ak+2为△ABC的三边,求k的取值范围.
19.对于一个各数位上的数字均不为0且互不相等的数m,将它各个数位上的数字分别平方后取其个位数字,得到一个新的数n,称n为m的“绝对疯癫数”,并规定f(m)=am﹣bn,(其中a、b为非零常数).例如;m=234,其各个数位上的数字分别平方后的数的个位数字分别是4、9、6,则234的“绝对疯癫数”n=496.已知f(7)=5,f(12)=10.
(1)计算f(269)的值:
(2)对于一个两位数s和一个三位数t,在s的中间位插入一个一位数k,得到一个新的三位数s',若s'是s的9倍,且t是s'的“绝对疯癫数”,求f(t)的最小值.
20.如图①是由边长为a的大正方形纸片剪去一个边长为b的小正方形后余下的图形.我们把纸片剪开后,拼成一个长方形(如图②).
(1)探究:上述操作能验证的等式的序号是
.
①a2+ab=a(a+b)
②a2﹣2ab+b2=(a﹣b)2③a2﹣b2=(a+b)(a﹣b)
(2)应用:利用你从(1)中选出的等式,完成下列各题:
①已知4x2﹣9y2=12,2x+3y=4,求2x﹣3y的值;
②计算(1﹣)×(1﹣)×(1﹣)×(1﹣)×…×(1﹣).
参考答案
一.选择题
1.解:4x2y和6xy3的公因式是2xy,
故选:A.
2.解:①2x2﹣x=x(2x﹣1),
②x2+4+4x=(x+2)2,
③x2+x﹣2=(x+2)(x﹣1),
④﹣x2+4x﹣4=﹣(x﹣2)2,
即①和②没有相同的因式,①和④没有相同的因式,②和③有相同的因式x+2,③和④没有相同的因式,
故选:C.
3.解:A、a2﹣b2符合平方差公式的特点,能用平方差公式进行因式分解;
B、﹣a2﹣b2两平方项符号相同,不能用平方差公式进行因式分解;
C、a2+b2两平方项符号相同,不能用平方差公式进行因式分解;
D、a2+2ab+b2是三项,不能用平方差公式进行因式分解.
故选:A.
4.解:∵x2+mx+9=(x+3)2=x2+6x+9,
∴m=6.
故选:D.
5.解:原式=[2﹣3(a﹣b)]2
=(2﹣3a﹣3b)2.
故选:D.
6.解:A、是整式的乘法,故此选项不符合题意;
B、把一个多项式化为几个整式的积的形式,故此选项符合题意;
C、没把一个多项式化为几个整式的积的形式,故此选项不符合题意;
D、把一个多项式化为整式与分式的积的形式,不是把一个多项式化为几个整式的积的形式,故此选项不符合题意;
故选:B.
7.解:(x2﹣y2)a2﹣(x2﹣y2)b2
=(x2﹣y2)(a2﹣b2)
=(x+y)(x﹣y)(a+b)(a﹣b),
由已知可得:我爱巴蜀,
故选:C.
8.解:将m2=4n+a与n2=4m+a相减得m2﹣n2=4n﹣4m,
(m+n)(m﹣n)=﹣4(m﹣n),
(m﹣n)(m+n+4)=0,
∵m≠n,
∴m+n+4=0,即m+n=﹣4,
∴m2+2mn+n2=(m+n)2=(﹣4)2=16.
故选:A.
9.解:若x2﹣mx﹣12(m为常数)可分解为两个一次因式的积,
m的值可能是﹣1,1,﹣4,4,11,﹣11.共有6个.
故选:C.
10.解:664﹣1
=(632+1)(632﹣1)
=(632+1)(616+1)(616﹣1)
=(632+1)(616+1)(68+1)(68﹣1)
=(632+1)(616+1)(68+1)(64+1)(64﹣1)
=(632+1)(616+1)(68+1)(64+1)(62+1)(62﹣1)
=(632+1)(616+1)(68+1)(64+1)×37×35.
故选:A.
二.填空题
11.解:3xy﹣6y=3y(x﹣2).
故答案为:3y(x﹣2).
12.解:设另一个因式是2x+n,
∴(x﹣3)(2x+n)=2x2+nx﹣6x﹣3n=2x2+mx+15,
∴﹣3n=15,n﹣6=m,
∴n=﹣5,m=﹣11,
故答案为﹣11.
13.关于x的二次三项式x2﹣4x+m在实数范围内不能分解因式,就是对应的二次方程x2﹣4x+m=0无实数根,
∴△=(﹣4)2﹣4m=16﹣4m<0,
∴m>4.
故答案为:m>4.
14.解:x2﹣5x﹣36
=(x﹣9)(x+4),
故答案为:(x﹣9)(x+4).
15.解:b4﹣b2﹣12=(b2﹣4)(b2+3)=(b+2)(b﹣2)(b2+3),
故答案为:(b+2)(b﹣2)(b2+3).
三.解答题
16.解:(1)x2+2x﹣15=(x+5)(x﹣3),
(2)3x2y2z﹣27y4z=3y2z(x2﹣9y2)=3y2z(x+3y)(x﹣3y),
(3)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.
17.解:(1)由图形直观得出,长为:(a+2b),宽为(a+b),
故答案为:(a+2b),(a+b);
(2)从总体看是边长为(a+b+c)的正方形,其面积为(a+b+c)2,
各个部分的面积和为a2+b2+c2+2ab+2bc+2ac,
因此有:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
故答案为:(a+b+c)2,a2+b2+c2+2ab+2bc+2ac,(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
(3)由(a+b+c)2=a2+b2+c2+2ab+2bc+2ac得,2ab+2bc+2ac=(a+b+c)2﹣(a2+b2+c2),
∵a+b+c=8,a2+b2+c2=26,
∴2ab+2bc+2ac=64﹣26=38,
∴ab+bc+ac=19.
18.解:(1)∵a1:32﹣12=8×1;
a2:52﹣32=8×2;
a3:72﹣52=8×3;…
∴a4:92﹣72=8×4;
(2)结果为:(2n+1)2﹣(2n﹣1)2=8n(n为正整数)
∵左边=(2n+1)2﹣(2n﹣1)2
=[(2n+1)+(2n﹣1)][(2n+1)﹣(2n﹣1)]
=4n×2
=8n
右边=8n,
∴左边=右边;
(3)由(2)可知:
∵ak=8k,ak+1=8(k+1),ak+2=8(k+2)
,
解得:k>1.
19.解:(1)7的“绝对疯癫数”是9,
∴m=7,n=9;
12的“绝对疯癫数”是14,
∴m=12,n=14;
∵f(m)=am﹣bn,
∴5=7a﹣9b,10=12a﹣14b,
∴a=2,b=1,
∵m=269的“绝对疯癫数”是n=461,
∴f(269)=2×269﹣1×461=77;
(2)设s的十位数字为a,个位数字为b,
由题意可知s'=100a+10k+b,
s=10a+b,
∵s'是s的9倍,
∴100a+10k+b=9(10a+b),
∴5(a+k)=4b,
∵0≤b≤9,
∴b=5,
∴a+k=4,
∵1≤a≤9,1≤k≤9,
∴满足条件的a与k为:
或或,
∴s'为135,315,
∵t是s'的“绝对疯癫数”,
∴t为195,915,
∴t的“绝对疯癫数”为115,115,
∵f(m)=2m﹣n,
∴f(195)=275,f(915)=1715,
∴f(t)的最小值为275.
20.解:(1)图①的面积可表示为a2﹣b2,
图②的面积可表示为(a+b)(a﹣b),
∵图①的面积=图②的面积,
∴上述操作能验证的等式是:a2﹣b2=(a+b)(a﹣b),
故答案为③;
(2)①∵4x2﹣9y2=12,
∴(2x+3y)(2x﹣3y)=12,
∵2x+3y=4,
∴2x﹣3y=12÷4=3;
②(1﹣)×(1﹣)×(1﹣)×(1﹣)×…×(1﹣)=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)===.
一.选择题
1.4x2y和6xy3的公因式是( )
A.2xy
B.3xy
C.2x2y
D.3xy3
2.多项式①2x2﹣x;②x2+4+4x;③x2+x﹣2;④﹣x2+4x﹣4,在分解因式结果含有相同因式的是( )
A.①和②
B.①和④
C.②和③
D.③和④
3.下列多项式中,能用平方差公式进行因式分解的是( )
A.a2﹣b2
B.﹣a2﹣b2
C.a2+b2
D.a2+2ab+b2
4.若x2+mx+9=(x+3)2,则m的值是( )
A.﹣18
B.18
C.﹣6
D.6
5.分解因式:4﹣12(a﹣b)+9(a﹣b)2=( )
A.(2+3a﹣3b)2
B.(2﹣3a﹣3b)2
C.(2+3a+3b)2
D.(2﹣3a+3b)2
6.下列四个等式从左到右的变形是因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.ab﹣a2=a(b﹣a)
C.x2+x﹣5=x(x+1)﹣5
D.x2+1=x(x+)
7.小明是一位密码翻译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:蜀、爱、我、巴、丽、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.我爱美
B.巴蜀美
C.我爱巴蜀
D.巴蜀美丽
8.已知m2=4n+a,n2=4m+a,m≠n,则m2+2mn+n2的值为( )
A.16
B.12
C.10
D.无法确定
9.二次三项式x2﹣mx﹣12(m是整数),在整数范围内可分为两个一次因式的积,则m的所有可能值有( )个.
A.4
B.5
C.6
D.8
10.已知664﹣1能被30﹣40之间的两个整数整除,则这两个整数是( )
A.35,37
B.35,36
C.34,38
D.36,37
二.填空题
11.因式分解3xy﹣6y=
.
12.已知m是常数,若x﹣3是2x2+mx+15的一个因式,则m的值为
.
13.如果关于x的二次三项式x2﹣4x+m在实数范围内不能分解因式,那么m的取值范围是
.
14.因式分解:x2﹣5x﹣36=
.
15.分解因式:b4﹣b2﹣12=
.
三.解答题
16.因式分解:
(1)x2+2x﹣15.
(2)3x2y2z﹣27y4z.
(3)(a2+1)2﹣4a2.
17.对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.
(1)对于等式(a+2b)(a+b)=a2+3ab+2b2,可以由图1进行解释:这个大长方形的长为
,宽为
,用长乘以宽可求得其面积.同时,大长方形的面积也等于3个长方形和3个正方形的面积之和.
(2)如图2,试用两种不同的方法求它的面积,你能得到什么数学等式?
方法1:
;
方法2:
;
数学等式:
;
(3)利用(2)中得到的数学等式,解决下列问题:已知a+b+c=8,a2+b2+c2=26,求ab+bc+ac的值.
18.观察下列关于自然数的等式:
a1:32﹣12=8×1;
a2:52﹣32=8×2;
a3:72﹣52=8×3;…
根据上述规律解决下列问题:
(1)写出第a4个等式:
;
(2)写出你猜想的第an个等式(用含n的式子表示),并验证其正确性;
(3)对于正整数k,若ak,ak+1,ak+2为△ABC的三边,求k的取值范围.
19.对于一个各数位上的数字均不为0且互不相等的数m,将它各个数位上的数字分别平方后取其个位数字,得到一个新的数n,称n为m的“绝对疯癫数”,并规定f(m)=am﹣bn,(其中a、b为非零常数).例如;m=234,其各个数位上的数字分别平方后的数的个位数字分别是4、9、6,则234的“绝对疯癫数”n=496.已知f(7)=5,f(12)=10.
(1)计算f(269)的值:
(2)对于一个两位数s和一个三位数t,在s的中间位插入一个一位数k,得到一个新的三位数s',若s'是s的9倍,且t是s'的“绝对疯癫数”,求f(t)的最小值.
20.如图①是由边长为a的大正方形纸片剪去一个边长为b的小正方形后余下的图形.我们把纸片剪开后,拼成一个长方形(如图②).
(1)探究:上述操作能验证的等式的序号是
.
①a2+ab=a(a+b)
②a2﹣2ab+b2=(a﹣b)2③a2﹣b2=(a+b)(a﹣b)
(2)应用:利用你从(1)中选出的等式,完成下列各题:
①已知4x2﹣9y2=12,2x+3y=4,求2x﹣3y的值;
②计算(1﹣)×(1﹣)×(1﹣)×(1﹣)×…×(1﹣).
参考答案
一.选择题
1.解:4x2y和6xy3的公因式是2xy,
故选:A.
2.解:①2x2﹣x=x(2x﹣1),
②x2+4+4x=(x+2)2,
③x2+x﹣2=(x+2)(x﹣1),
④﹣x2+4x﹣4=﹣(x﹣2)2,
即①和②没有相同的因式,①和④没有相同的因式,②和③有相同的因式x+2,③和④没有相同的因式,
故选:C.
3.解:A、a2﹣b2符合平方差公式的特点,能用平方差公式进行因式分解;
B、﹣a2﹣b2两平方项符号相同,不能用平方差公式进行因式分解;
C、a2+b2两平方项符号相同,不能用平方差公式进行因式分解;
D、a2+2ab+b2是三项,不能用平方差公式进行因式分解.
故选:A.
4.解:∵x2+mx+9=(x+3)2=x2+6x+9,
∴m=6.
故选:D.
5.解:原式=[2﹣3(a﹣b)]2
=(2﹣3a﹣3b)2.
故选:D.
6.解:A、是整式的乘法,故此选项不符合题意;
B、把一个多项式化为几个整式的积的形式,故此选项符合题意;
C、没把一个多项式化为几个整式的积的形式,故此选项不符合题意;
D、把一个多项式化为整式与分式的积的形式,不是把一个多项式化为几个整式的积的形式,故此选项不符合题意;
故选:B.
7.解:(x2﹣y2)a2﹣(x2﹣y2)b2
=(x2﹣y2)(a2﹣b2)
=(x+y)(x﹣y)(a+b)(a﹣b),
由已知可得:我爱巴蜀,
故选:C.
8.解:将m2=4n+a与n2=4m+a相减得m2﹣n2=4n﹣4m,
(m+n)(m﹣n)=﹣4(m﹣n),
(m﹣n)(m+n+4)=0,
∵m≠n,
∴m+n+4=0,即m+n=﹣4,
∴m2+2mn+n2=(m+n)2=(﹣4)2=16.
故选:A.
9.解:若x2﹣mx﹣12(m为常数)可分解为两个一次因式的积,
m的值可能是﹣1,1,﹣4,4,11,﹣11.共有6个.
故选:C.
10.解:664﹣1
=(632+1)(632﹣1)
=(632+1)(616+1)(616﹣1)
=(632+1)(616+1)(68+1)(68﹣1)
=(632+1)(616+1)(68+1)(64+1)(64﹣1)
=(632+1)(616+1)(68+1)(64+1)(62+1)(62﹣1)
=(632+1)(616+1)(68+1)(64+1)×37×35.
故选:A.
二.填空题
11.解:3xy﹣6y=3y(x﹣2).
故答案为:3y(x﹣2).
12.解:设另一个因式是2x+n,
∴(x﹣3)(2x+n)=2x2+nx﹣6x﹣3n=2x2+mx+15,
∴﹣3n=15,n﹣6=m,
∴n=﹣5,m=﹣11,
故答案为﹣11.
13.关于x的二次三项式x2﹣4x+m在实数范围内不能分解因式,就是对应的二次方程x2﹣4x+m=0无实数根,
∴△=(﹣4)2﹣4m=16﹣4m<0,
∴m>4.
故答案为:m>4.
14.解:x2﹣5x﹣36
=(x﹣9)(x+4),
故答案为:(x﹣9)(x+4).
15.解:b4﹣b2﹣12=(b2﹣4)(b2+3)=(b+2)(b﹣2)(b2+3),
故答案为:(b+2)(b﹣2)(b2+3).
三.解答题
16.解:(1)x2+2x﹣15=(x+5)(x﹣3),
(2)3x2y2z﹣27y4z=3y2z(x2﹣9y2)=3y2z(x+3y)(x﹣3y),
(3)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.
17.解:(1)由图形直观得出,长为:(a+2b),宽为(a+b),
故答案为:(a+2b),(a+b);
(2)从总体看是边长为(a+b+c)的正方形,其面积为(a+b+c)2,
各个部分的面积和为a2+b2+c2+2ab+2bc+2ac,
因此有:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
故答案为:(a+b+c)2,a2+b2+c2+2ab+2bc+2ac,(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
(3)由(a+b+c)2=a2+b2+c2+2ab+2bc+2ac得,2ab+2bc+2ac=(a+b+c)2﹣(a2+b2+c2),
∵a+b+c=8,a2+b2+c2=26,
∴2ab+2bc+2ac=64﹣26=38,
∴ab+bc+ac=19.
18.解:(1)∵a1:32﹣12=8×1;
a2:52﹣32=8×2;
a3:72﹣52=8×3;…
∴a4:92﹣72=8×4;
(2)结果为:(2n+1)2﹣(2n﹣1)2=8n(n为正整数)
∵左边=(2n+1)2﹣(2n﹣1)2
=[(2n+1)+(2n﹣1)][(2n+1)﹣(2n﹣1)]
=4n×2
=8n
右边=8n,
∴左边=右边;
(3)由(2)可知:
∵ak=8k,ak+1=8(k+1),ak+2=8(k+2)
,
解得:k>1.
19.解:(1)7的“绝对疯癫数”是9,
∴m=7,n=9;
12的“绝对疯癫数”是14,
∴m=12,n=14;
∵f(m)=am﹣bn,
∴5=7a﹣9b,10=12a﹣14b,
∴a=2,b=1,
∵m=269的“绝对疯癫数”是n=461,
∴f(269)=2×269﹣1×461=77;
(2)设s的十位数字为a,个位数字为b,
由题意可知s'=100a+10k+b,
s=10a+b,
∵s'是s的9倍,
∴100a+10k+b=9(10a+b),
∴5(a+k)=4b,
∵0≤b≤9,
∴b=5,
∴a+k=4,
∵1≤a≤9,1≤k≤9,
∴满足条件的a与k为:
或或,
∴s'为135,315,
∵t是s'的“绝对疯癫数”,
∴t为195,915,
∴t的“绝对疯癫数”为115,115,
∵f(m)=2m﹣n,
∴f(195)=275,f(915)=1715,
∴f(t)的最小值为275.
20.解:(1)图①的面积可表示为a2﹣b2,
图②的面积可表示为(a+b)(a﹣b),
∵图①的面积=图②的面积,
∴上述操作能验证的等式是:a2﹣b2=(a+b)(a﹣b),
故答案为③;
(2)①∵4x2﹣9y2=12,
∴(2x+3y)(2x﹣3y)=12,
∵2x+3y=4,
∴2x﹣3y=12÷4=3;
②(1﹣)×(1﹣)×(1﹣)×(1﹣)×…×(1﹣)=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)===.
