人教版八年级上册课时练:15.3分式方程 实际应用解答题提优(四)(Word版 含解析)
文档属性
| 名称 | 人教版八年级上册课时练:15.3分式方程 实际应用解答题提优(四)(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 42.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:00:00 | ||
图片预览



文档简介
人教版八上课时练:第十五章《分式》
实际应用解答题提优(四)
1.在数学课上,老师出了这样一道题:甲、乙两地相距1200千米,乘高铁列车从甲地到乙地比乘特快列车少用8小时,已知高铁列车的平均行驶速度是特快列车的3倍,求特快列车从甲地到乙地的时间.
2.张康和李健两名运动爱好者周末相约到丹江环库绿道进行跑步锻炼.
(1)周日早上6点,张康和李健同时从家出发,分别骑自行车和步行到离家距离分别为6千米和1.6千米的绿道环库路入口汇合,结果同时到达,且张康每分钟比李健每分钟多行220米,求张康和李健的速度分别是多少米/分?
(2)两人到达绿道后约定先跑6千米再休息,李健的跑步速度是张康跑步速度的a倍,两人在同起点,同时出发,结果李健先到目的地b分钟.
①当a=1.2,b=6时,求李健跑了多少分钟?
②求张康的跑步速度多少米/分?(直接用含a,b的式子表示)
3.学校开展“书香校园”活动,购买了一批图书.已知购买科普类图书花费了10000元,购买文学类图书花费了9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量比购买文学类图书数量少100本,科普类图书平均每本的价格是多少元?
4.王老师到一家文具店给该校学生购买2B铅笔,文具店规定一次购买400支以上,可享受8折优惠.若该校学生每人购买一支,不能享受8折优惠,需要付款1936元;王老师想了想发现多买88支后,不仅可以享受8折优惠,而且同样只要付1936元.该校学生有多少人?
5.有一种用来画圆的工具板(如图所示),工具板长21cm,上面依次排列着大小不等的五个圆(孔),其中最大圆的直径为3cm,其余圆的直径从左到右依次递减xcm.最大圆的左侧距工具板左侧边缘1.5cm,最小圆的右侧距工具板右侧边缘1.5cm,相邻两圆的间距d均相等.
(1)用含x的代数式表达出其余四个圆的直径长;
(2)若最大圆与最小圆的直径之比为15:11,求相邻两圆的间距.
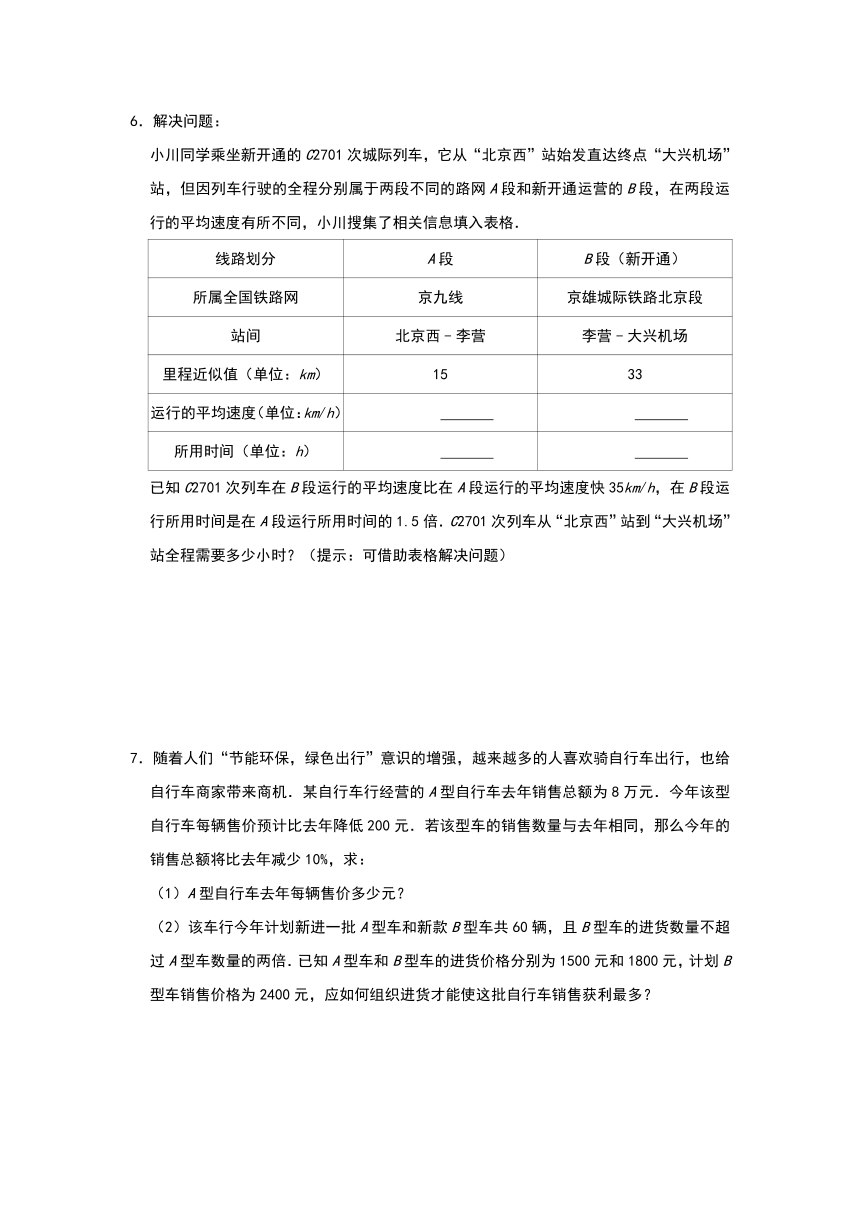
6.解决问题:
小川同学乘坐新开通的C2701次城际列车,它从“北京西”站始发直达终点“大兴机场”站,但因列车行驶的全程分别属于两段不同的路网A段和新开通运营的B段,在两段运行的平均速度有所不同,小川搜集了相关信息填入表格.
线路划分
A段
B段(新开通)
所属全国铁路网
京九线
京雄城际铁路北京段
站间
北京西﹣李营
李营﹣大兴机场
里程近似值(单位:km)
15
33
运行的平均速度(单位:km/h)
所用时间(单位:h)
已知C2701次列车在B段运行的平均速度比在A段运行的平均速度快35km/h,在B段运行所用时间是在A段运行所用时间的1.5倍.C2701次列车从“北京西”站到“大兴机场”站全程需要多少小时?(提示:可借助表格解决问题)
7.随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
8.端午节到了,某商场出售A,B两种粽子礼盒,其中B种礼盒单价是A种礼盒的1.5倍,已知用2000元购买A种礼盒的数量,比用2400元购买B种礼盒的数量多5盒,求A,B两种粽子礼盒的单价分别是多少元?
9.某工厂有甲、乙两台机器加工同一种零件,已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个,甲加工80个零件与乙加工100个零件的所用时间相等.求甲、乙两台机器每小时分别加工零件多少个?
10.某商店用8000元第一次购进一批服装,售完后又用17600元购进同样的服装,件数是第一次件数的2倍,第二次比第一次每件贵了4元.
(1)商店两次共购进服装多少件?
(2)第一次以60元/件很快销售完毕,第二次也以同样的价格销售,最后还剩100件,然后又以6折的价格很快售完,请问该商店第二批服装的盈亏情况如何?
参考答案
1.解法1:
解:设高铁列车从甲地到乙地的时间为yh,则特快列车从甲地到乙地的时间为(y+8)h,
根据题意得,
解这个方程得
y=4.
经检验,y=4是原分式方程的根,
则y+8=12.
答:特快列车从甲地到乙地的时间为12h.
解法2:
解:设特快列车的平均速度为x
km/h,则高铁列车的平均速度为3x
km/h,
根据题意得,
解这个方程得x=100.
经检验,x=100是原分式方程的根,
则.
答:特快列车从甲地到乙地的时间为12h.
2.解:(1)设李健的速度为x米/分,则张康的速度为(x+220)米/分,
根据题意,得:,
解得:x=80,
经检验,x=80是原方程的根,且符合题意,
∴x+220=300.
答:李健的速度为80米/分,张康的速度为300米/分.
(2)①∵a=1.2,b=6,
∴6÷(1.2﹣1)=30(分钟).
答:李健跑了30分钟;
②李健跑了的时间为分钟,
张康跑了的时间为分钟,
张康的跑步速度为米/分.
3.解:设科普类图书平均每本的价格是x元,则文学类图书平均每本的价格为(x﹣5)元,根据题意可得:
=﹣100,
解得:x=20,
经检验得:x=20是原方程的根,
答:科普类图书平均每本的价格是20元.
4.解:设该校学生有x人,
根据题意,列方程得:×0.8=,
整理得:0.8(x+88)=x,
解之得:x=352,
经检验x=352是原方程的解,
答:这个学校的学生有352人.
5.解:(1)其余四个圆的直径依次为:
(3﹣x)cm,(3﹣2x)cm,(3﹣3x)cm,(3﹣4x)cm,
(2)由题意可知:=,
解得,x=0.2cm,
经检验:x=0.2是原方程的解,
∴2×1.5+[3+(3﹣x)+(3﹣2x)(3﹣3x)+(3﹣4x)]+4d=21.
∴d=1.25cm.
答:相邻两圆的间距为1.25cm.
6.解:设C2701次列车在A段运行所用时间为th,则在B段运行所用时间为1.5th,在A段上行驶的速度为km/h,在B段上行驶的速度为km/h,
根据题意列出方程,
,
解得,t=0.2,
经检验,原分式方程的解为t=0.2,也符合实际意义,
∴C2701次列车从“北京西”站到“大兴机场”站全程需要的时间为:
t+1.5t=2.5t=2.5×0.2=0.5(h),
答:C2701次列车从“北京西”站到“大兴机场”站全程需要0.5h.
故答案为:;;t;1.5t.
7.解:(1)设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,由题意,得
=,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元;
(2)设今年新进A型车a辆,则B型车(60﹣a)辆,获利y元,由题意,得
y=(2000﹣200﹣1500)a+(2400﹣1800)(60﹣a),
y=﹣300a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60﹣a≤2a,
∴a≥20.
∵y=﹣300a+36000.
∴k=﹣300<0,
∴y随a的增大而减小.
∴a=20时,y有最大值,
∴B型车的数量为:60﹣20=40(辆).
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
8.解:设A种粽子礼盒的单价是x元,则B种粽子礼盒的单价是1.5x元,由题意得:
,
解得:x=80,
经检验,x=80是原方程的解,且符合题意,
∴1.5x=120.
答:A种粽子礼盒的单价是80元,则B种粽子礼盒的单价是120元.
9.解:设甲机器每小时加工零件x个,则乙机器每小时加工零件(36﹣x)个,
根据题意得:=,
解得:x=16,
经检验,x=16是原方程的解,
∴36﹣x=36﹣16=20.
答:甲机器每小时加工零件16个,乙机器每小时加工零件20个.
10.解:(1)设第一次购进服装x件,则第二次购进服装2x件,
依题意,得:﹣=4,
解得:x=200,
经检验,x=200是原方程的解,且符合题意,
∴x+2x=600.
答:商店两次共购进服装600件.
(2)60×(200×2﹣100)+60×0.6×100﹣17600=4000(元).
答:该商店第二批服装共盈利4000元.
实际应用解答题提优(四)
1.在数学课上,老师出了这样一道题:甲、乙两地相距1200千米,乘高铁列车从甲地到乙地比乘特快列车少用8小时,已知高铁列车的平均行驶速度是特快列车的3倍,求特快列车从甲地到乙地的时间.
2.张康和李健两名运动爱好者周末相约到丹江环库绿道进行跑步锻炼.
(1)周日早上6点,张康和李健同时从家出发,分别骑自行车和步行到离家距离分别为6千米和1.6千米的绿道环库路入口汇合,结果同时到达,且张康每分钟比李健每分钟多行220米,求张康和李健的速度分别是多少米/分?
(2)两人到达绿道后约定先跑6千米再休息,李健的跑步速度是张康跑步速度的a倍,两人在同起点,同时出发,结果李健先到目的地b分钟.
①当a=1.2,b=6时,求李健跑了多少分钟?
②求张康的跑步速度多少米/分?(直接用含a,b的式子表示)
3.学校开展“书香校园”活动,购买了一批图书.已知购买科普类图书花费了10000元,购买文学类图书花费了9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量比购买文学类图书数量少100本,科普类图书平均每本的价格是多少元?
4.王老师到一家文具店给该校学生购买2B铅笔,文具店规定一次购买400支以上,可享受8折优惠.若该校学生每人购买一支,不能享受8折优惠,需要付款1936元;王老师想了想发现多买88支后,不仅可以享受8折优惠,而且同样只要付1936元.该校学生有多少人?
5.有一种用来画圆的工具板(如图所示),工具板长21cm,上面依次排列着大小不等的五个圆(孔),其中最大圆的直径为3cm,其余圆的直径从左到右依次递减xcm.最大圆的左侧距工具板左侧边缘1.5cm,最小圆的右侧距工具板右侧边缘1.5cm,相邻两圆的间距d均相等.
(1)用含x的代数式表达出其余四个圆的直径长;
(2)若最大圆与最小圆的直径之比为15:11,求相邻两圆的间距.
6.解决问题:
小川同学乘坐新开通的C2701次城际列车,它从“北京西”站始发直达终点“大兴机场”站,但因列车行驶的全程分别属于两段不同的路网A段和新开通运营的B段,在两段运行的平均速度有所不同,小川搜集了相关信息填入表格.
线路划分
A段
B段(新开通)
所属全国铁路网
京九线
京雄城际铁路北京段
站间
北京西﹣李营
李营﹣大兴机场
里程近似值(单位:km)
15
33
运行的平均速度(单位:km/h)
所用时间(单位:h)
已知C2701次列车在B段运行的平均速度比在A段运行的平均速度快35km/h,在B段运行所用时间是在A段运行所用时间的1.5倍.C2701次列车从“北京西”站到“大兴机场”站全程需要多少小时?(提示:可借助表格解决问题)
7.随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
8.端午节到了,某商场出售A,B两种粽子礼盒,其中B种礼盒单价是A种礼盒的1.5倍,已知用2000元购买A种礼盒的数量,比用2400元购买B种礼盒的数量多5盒,求A,B两种粽子礼盒的单价分别是多少元?
9.某工厂有甲、乙两台机器加工同一种零件,已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个,甲加工80个零件与乙加工100个零件的所用时间相等.求甲、乙两台机器每小时分别加工零件多少个?
10.某商店用8000元第一次购进一批服装,售完后又用17600元购进同样的服装,件数是第一次件数的2倍,第二次比第一次每件贵了4元.
(1)商店两次共购进服装多少件?
(2)第一次以60元/件很快销售完毕,第二次也以同样的价格销售,最后还剩100件,然后又以6折的价格很快售完,请问该商店第二批服装的盈亏情况如何?
参考答案
1.解法1:
解:设高铁列车从甲地到乙地的时间为yh,则特快列车从甲地到乙地的时间为(y+8)h,
根据题意得,
解这个方程得
y=4.
经检验,y=4是原分式方程的根,
则y+8=12.
答:特快列车从甲地到乙地的时间为12h.
解法2:
解:设特快列车的平均速度为x
km/h,则高铁列车的平均速度为3x
km/h,
根据题意得,
解这个方程得x=100.
经检验,x=100是原分式方程的根,
则.
答:特快列车从甲地到乙地的时间为12h.
2.解:(1)设李健的速度为x米/分,则张康的速度为(x+220)米/分,
根据题意,得:,
解得:x=80,
经检验,x=80是原方程的根,且符合题意,
∴x+220=300.
答:李健的速度为80米/分,张康的速度为300米/分.
(2)①∵a=1.2,b=6,
∴6÷(1.2﹣1)=30(分钟).
答:李健跑了30分钟;
②李健跑了的时间为分钟,
张康跑了的时间为分钟,
张康的跑步速度为米/分.
3.解:设科普类图书平均每本的价格是x元,则文学类图书平均每本的价格为(x﹣5)元,根据题意可得:
=﹣100,
解得:x=20,
经检验得:x=20是原方程的根,
答:科普类图书平均每本的价格是20元.
4.解:设该校学生有x人,
根据题意,列方程得:×0.8=,
整理得:0.8(x+88)=x,
解之得:x=352,
经检验x=352是原方程的解,
答:这个学校的学生有352人.
5.解:(1)其余四个圆的直径依次为:
(3﹣x)cm,(3﹣2x)cm,(3﹣3x)cm,(3﹣4x)cm,
(2)由题意可知:=,
解得,x=0.2cm,
经检验:x=0.2是原方程的解,
∴2×1.5+[3+(3﹣x)+(3﹣2x)(3﹣3x)+(3﹣4x)]+4d=21.
∴d=1.25cm.
答:相邻两圆的间距为1.25cm.
6.解:设C2701次列车在A段运行所用时间为th,则在B段运行所用时间为1.5th,在A段上行驶的速度为km/h,在B段上行驶的速度为km/h,
根据题意列出方程,
,
解得,t=0.2,
经检验,原分式方程的解为t=0.2,也符合实际意义,
∴C2701次列车从“北京西”站到“大兴机场”站全程需要的时间为:
t+1.5t=2.5t=2.5×0.2=0.5(h),
答:C2701次列车从“北京西”站到“大兴机场”站全程需要0.5h.
故答案为:;;t;1.5t.
7.解:(1)设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,由题意,得
=,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元;
(2)设今年新进A型车a辆,则B型车(60﹣a)辆,获利y元,由题意,得
y=(2000﹣200﹣1500)a+(2400﹣1800)(60﹣a),
y=﹣300a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60﹣a≤2a,
∴a≥20.
∵y=﹣300a+36000.
∴k=﹣300<0,
∴y随a的增大而减小.
∴a=20时,y有最大值,
∴B型车的数量为:60﹣20=40(辆).
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
8.解:设A种粽子礼盒的单价是x元,则B种粽子礼盒的单价是1.5x元,由题意得:
,
解得:x=80,
经检验,x=80是原方程的解,且符合题意,
∴1.5x=120.
答:A种粽子礼盒的单价是80元,则B种粽子礼盒的单价是120元.
9.解:设甲机器每小时加工零件x个,则乙机器每小时加工零件(36﹣x)个,
根据题意得:=,
解得:x=16,
经检验,x=16是原方程的解,
∴36﹣x=36﹣16=20.
答:甲机器每小时加工零件16个,乙机器每小时加工零件20个.
10.解:(1)设第一次购进服装x件,则第二次购进服装2x件,
依题意,得:﹣=4,
解得:x=200,
经检验,x=200是原方程的解,且符合题意,
∴x+2x=600.
答:商店两次共购进服装600件.
(2)60×(200×2﹣100)+60×0.6×100﹣17600=4000(元).
答:该商店第二批服装共盈利4000元.
